いろいろご教示をいただきました。ありがとうございます。まだまだ不十分なところがありますが,これからも見直していきたいと思いますので,お気づきのことがありましたらお知らせいただければ幸いです。とりあえず現段階でのお薦めの方法はnlmeパッケージによる非線形最小二乗法です。
だんだんごたごたしてきましたので,主にコベル法を扱うスペクトルのフィット1からこのページを独立させました。それでもごたごたしてきたので,先に実例を見ていただくほうがいいかもしれません:例1,例2,例3,例4
同じ問題を非線形の重み付き最小二乗法で解いてみます。Rには nls()
という非線形最小二乗法の関数が含まれています(デフォルトのアルゴリズムはGauss-Newton法)。重みは分散の逆数を与えればいいのですが,ポアソン分布の性質から分散はカウント値の期待値に等しいので,これを実際のカウント値で代用します。
fit = nls(sp ~ c + d*ch + e*dnorm((ch-m)/s),
start=list(c=50,d=-0.2,e=100,m=50,s=5), weights=1/sp)
結果の概略を見るには単に fit と打ち込みます:
> fit
Nonlinear regression model
model: sp ~ c + d * ch + e * dnorm((ch - m)/s)
data: parent.frame()
c d e m s
49.6647 -0.2189 114.3944 49.9199 4.7445
weighted residual sum-of-squares: 79.94
Number of iterations to convergence: 5
Achieved convergence tolerance: 4.857e-06
係数とピークのカウントは次のようにして求められます。
> a = coef(fit)
> a
c d e m s
49.6647224 -0.2188877 114.3944350 49.9199274 4.7445441
> sum(a['e']*dnorm((ch-a['m'])/a['s']))
[1] 542.7494
各パラメータの推定誤差などは summary() で調べられます:
> summary(fit)
Formula: sp ~ c + d * ch + e * dnorm((ch - m)/s)
Parameters:
Estimate Std. Error t value Pr(>|t|)
c 49.66472 1.30837 37.96 <2e-16 ***
d -0.21889 0.02011 -10.89 <2e-16 ***
e 114.39443 8.60629 13.29 <2e-16 ***
m 49.91993 0.36836 135.52 <2e-16 ***
s 4.74454 0.36406 13.03 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.9222 on 94 degrees of freedom
Number of iterations to convergence: 5
Achieved convergence tolerance: 4.857e-06
共分散行列は vcov() です:
> vcov(fit)
c d e m s
c 1.71184306 -0.0227252330 -0.890443698 0.0346645848 -0.0919897866
d -0.02272523 0.0004042742 0.004565929 -0.0006519183 0.0003569787
e -0.89044370 0.0045659288 74.068175203 -0.0212548830 -1.6485651131
m 0.03466458 -0.0006519183 -0.021254883 0.1356873238 -0.0009086423
s -0.09198979 0.0003569787 -1.648565113 -0.0009086423 0.1325383070
これから単純に誤差を求めると次のように約40になります:
> v = vcov(fit)
> a = coef(fit)
> 542.7494 * sqrt(v[3,3]/a[3]^2 + v[5,5]/a[5]^2 + 2*v[3,5]/(a[3]*a[5]))
e
40.15244
この最後の式は積の誤差の考え方を使ったものです。
非線形最小二乗法で求めたカウントの誤差の程度を推定するために,簡単なシミュレーションをしてみましょう。最小化の計算が収束しない場合でもシミュレーション全体が終了しないように,nls() に warnOnly=TRUE というオプションを与えておきます。
bg = function(x) { 50 - 0.2 * x }
pe = function(x) { 100 * dnorm((x-50)/5) }
foo = function() {
sp = rpois(99, bg(ch)+pe(ch))
fit = nls(sp ~ c + d*ch + e*dnorm((ch-m)/s),
start=list(c=50,d=-0.2,e=100,m=50,s=5), weights=1/sp,
control=list(warnOnly=TRUE))
a = coef(fit)
sum(a['e']*dnorm((ch-a['m'])/a['s']))
}
r = replicate(10000, foo()) # 10000回繰り返す
mean(r)
sd(r)
平均505程度,標準偏差46程度のようです。想定した正解より少しだけ大きいのが気になります。
正しいモデルがわかっていなくても,得られたデータからのリサンプリングによりシミュレーションをするブートストラップ法で誤差を推定してみます。
library(boot)
data = data.frame(ch=ch, sp=sp)
foo = function(data, k) {
fit = nls(sp[k] ~ c + d*ch[k] + e*dnorm((ch[k]-m)/s), data,
start=list(c=50,d=-0.2,e=100,m=50,s=5), weights=1/sp[k],
control=list(warnOnly=TRUE))
a = coef(fit)
sum(a['e']*dnorm((ch-a['m'])/a['s']))
}
b = boot(data, foo, R=999)
b
途中で「繰り返し数が最大値 50 を超えました」という警告が何度か出ますが,無視します。結果は次のようになりました(乱数によるシミュレーションですので結果は毎回異なります):
ORDINARY NONPARAMETRIC BOOTSTRAP
Call:
boot(data = data, statistic = foo, R = 999)
Bootstrap Statistics :
original bias std. error
t1* 542.7494 6.508727 46.50908
誤差は46.5程度であることがわかります。今回は正しいモデルを使ったシミュレーションの結果とたまたま良く一致しましたが,一般にはおおまかな推定値としてとらえてください。
ついでに plot(b) と打ち込んでブートストラップシミュレーションの結果をプロットしてみます:

わざわざブートストラップ法を使わなくても,測定データをポアソン乱数で置き換えるだけでも同様な誤差推定ができそうです。
foo = function() {
sp1 = rpois(99, sp)
fit = nls(sp1 ~ c + d*ch + e*dnorm((ch-m)/s),
start=list(c=50,d=-0.2,e=100,m=50,s=5), weights=1/sp,
control=list(warnOnly=TRUE))
a = coef(fit)
sum(a['e']*dnorm((ch-a['m'])/a['s']))
}
r = replicate(1000, foo())
sd(r)
この方法で得た誤差は 44.8 でした(乱数によるシミュレーションですから毎回異なります)。こちらのほうがブートストラップ法と比べて極端なデータが出にくいので,非線形最小二乗法が収束しないトラブルも起こりにくいように思います。
非線形最小二乗法の重みは,上の nls() を使った例では,測定されたカウント数の逆数を使いました。しかし,本来はフィットした関数値の逆数にするほうが理にかなっています。確率変数 X の分散 V(X) に等しいのは X の実現値ではなく期待値 E(X) ですから。しかしこれは nls() では簡単にできません。強いてするなら次のようにループを使わなければなりません。
w = 1 / sp
for (i in 1:10) {
fit = nls(sp ~ c + d*ch + e*dnorm((ch-m)/s),
start=list(c=50,d=-0.2,e=100,m=50,s=5), weights=w,
control=list(warnOnly=TRUE))
a = coef(fit)
print(a)
w = 1 / (a['c'] + a['d']*ch + a['e']*dnorm((ch-a['m'])/a['s']))
}
このループは厳密には sum((sp - fitted(fit))^2 / fitted(fit))
を最小化するものではありません(TODO:考察)。
start の値も毎回更新すると収束が速くなる理屈ですが,実際には数値微分が失敗するようです。数値微分ではなく数式微分を使うこともできます(deriv のヘルプ参照)。
これと同じことをするのがnlme(nonlinear mixed effects)パッケージの gnls()(generalized nonlinear least-squares)という関数です(文献 [1])。重みとして varPower(fixed=0.5) を与えればフィットした値を分散と仮定します(つまりフィットした値の逆数を重みとした非線形最小二乗法になります)。
library(nlme)
data = data.frame(sp=sp, ch=ch)
fit2 = gnls(sp ~ c + d*ch + e*dnorm((ch-m)/s), data=data,
start=list(c=50,d=-0.2,e=100,m=50,s=5),
weights=varPower(fixed=0.5),
control=list(nlsTol=1e-4))
係数や誤差を求めます:
> a = coef(fit2) # 係数
> a
c d e m s
50.4241404 -0.2186549 113.5275437 49.8477760 4.8125038
> sum(a['e']*dnorm((ch-a['m'])/a['s']))
[1] 546.3517
> v = vcov(fit2) # 共分散行列
> sqrt(v['e','e']/a['e']^2 + v['s','s']/a['s']^2 + 2*v['e','s']/(a['e']*a['s']))
e
0.0740356 # 正味の計数の相対誤差(1σ相当)
> 546.3517 * 0.0740356
[1] 40.44948 # 正味の計数の誤差(1σ相当)
誤差の分散については,山の高さ v['e','e']/a['e']^2 と幅 v['s','s']/a['s']^2 と負の共分散 2*v['e','s']/(a['e']*a['s']) の絶対値とがほぼ等しいので,例えば幅を固定して山の高さの誤差だけを考えても良さそうです。
この方法のおもしろい点は,総カウント数 sum(sp) とフィットした値の合計 sum(fitted(fit2)) が(数値計算の誤差範囲内で)一致することです。これは,ピークの正確な形より総カウント数に意味がある場合に,非常に有利な条件となります(一般にある条件を満たすPoisson回帰でこれは成り立ちます。例えば文献[3]のp.183練習問題9.1参照)。
ただ,現バージョンの gnls() は収束の判定が少し甘いようです。上の計算では少し条件を厳しくするために gnls() に control=list(nlsTol=1e-4) というオプションを与えています(デフォルト値は nlsTol=1e-3)。ただ,こうすると収束しなくなることがあるので,適宜加減してください。
次の図は,いろいろな varPower(fixed=?) の値について,フィットした値の合計を示したものです。黒丸はデフォルトの収束条件,青丸は収束条件を厳しくした場合です。たまたま0.25を境にして反復数が変わるようで,段差ができていますが,実用上問題になるような計算誤差ではありません。
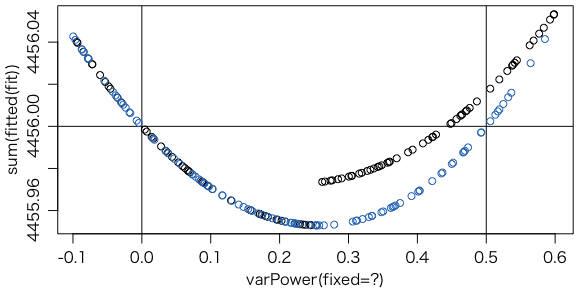
上の図は次のようにして描きました:
foo = function(x) {
fit = gnls(sp ~ c + d*ch + e*dnorm((ch-m)/s), data=data,
start=list(c=50,d=-0.2,e=100,m=50,s=5),
weights=varPower(fixed=x))
return(sum(fitted(fit)))
}
r = replicate(100, { t = runif(1,-0.1,0.6); list(t,foo(t)) })
plot(r[1,], r[2,], xlab="varPower(fixed=?)", ylab="sum(fitted(fit))")
abline(h=4456)
abline(v=0)
abline(v=0.5)
foo = function(x) {
fit = gnls(sp ~ c + d*ch + e*dnorm((ch-m)/s), data=data,
start=list(c=50,d=-0.2,e=100,m=50,s=5),
weights=varPower(fixed=x),
control=list(nlsTol=ifelse(x<0.2, 1e-3, 1e-4)))
return(sum(fitted(fit)))
}
r = replicate(100, { t = runif(1,-0.1,0.6); list(t,foo(t)) })
points(r[1,], r[2,], col="#0068b7") # 青丸
nlmeパッケージの非線形最小二乗法 gnls() で求めたカウントの誤差の程度を推定するために,簡単なシミュレーションをしてみましょう。
bg = function(x) { 50 - 0.2 * x }
pe = function(x) { 100 * dnorm((x-50)/5) }
foo = function() {
sp = rpois(99, bg(ch)+pe(ch))
data = data.frame(sp=sp, ch=ch)
fit = gnls(sp ~ c + d*ch + e*dnorm((ch-m)/s),
data=data,
start=list(c=50,d=-0.2,e=100,m=50,s=5),
weights=varPower(fixed=0.5),
control=list(nlsTol=1e-4))
a = coef(fit)
sum(a['e']*dnorm((ch-a['m'])/a['s']))
}
r = replicate(10000, foo()) # 10000回繰り返す
mean(r)
# [1] 502.1784
sd(r)
# [1] 44.76659
平均500程度,標準偏差45程度です。他の方法より若干良いようです。
他の方法として,ポアソン分布を正規分布に近い形に変形する変換(variance stabilizing transform)も使えそうです。具体的には sqrt(x + 3/8) のような変換がよく使われています。
ピークの幅と位置が定まれば,単純な(線形)Poisson回帰の問題になり,glm() で解けます。この場合,定数項は自動的に入りますので,モデル式 sp ~ ... には入れません。
fit = glm(sp ~ ch + dnorm((ch-50)/5), data=data, family=poisson(link="identity"))
summary(fit) と打ち込むと,係数や誤差などたくさん出力されます。ピークカウントを出すために必要なのは3番目の係数(1番目は定数項,2番目は ch の係数)ですので,それだけを見るためには summary(fit)$coefficients[3,]
とすればいいのですが,この中でさらに1番目の要素が係数,2番目の要素が誤差ですので,この二つだけが欲しいなら summary(fit)$coefficients[3,1:2]
とします。それに dnorm((ch-50)/5) の積分値を掛ければ実際のピークカウントと誤差が得られます:
> summary(fit)$coefficients[3,1:2]*sum(dnorm((ch-50)/5))
Estimate Std. Error
556.0018 38.7522
Estimate や Std. Error という名前が出力されるのが邪魔な場合は as.numeric(...)
で囲めばいいでしょう。
Rには,より一般的な最小化のための optim() という関数もあります。また,パッケージ minpack.lm には,Levenberg-Marquardt法を使った nls.lm() という関数があります。
次の例は optim() を使ってPoisson回帰の対数尤度を最大にするパラメータを求めています。
foo = function(x) {
c = x[1]
d = x[2]
e = x[3]
m = x[4]
s = x[5]
y = c + d * ch + e * dnorm((ch-m)/s)
-sum(sp * log(y) - y, na.rm=TRUE)
}
optim(c(50,-0.2,110,50,5), foo)
# [1] 50.434828 -0.218678 113.557225 49.848596 4.806925
optim(c(50,-0.2,110,50,5), foo, control=list(maxit=10000, reltol=1e-16))
# [1] 50.4241695 -0.2186555 113.5276389 49.8477594 4.8125010
次の例は optim() を使ってPoisson回帰でdeviance(逸脱度)を最小にするピークの中心と幅を求めています。
foo = function(x) {
m = x[1]
s = x[2]
fit = glm(sp ~ ch + dnorm((ch-m)/s), data=data, family=poisson(link="identity"))
fit$deviance # 逸脱度を返す
}
optim(c(50,5), foo)
なお,glm() が収束しないときは,オプションで初期値を start=c(定数項,第1の係数,第2の係数) の要領で与えます:
fit = glm(sp ~ ch + dnorm((ch-m)/s), data=data, family=poisson(link="identity"),
start=c(50,-0.2,100))
これらの方法は本当にポアソン分布を最尤法でフィットするので,個々のビン(階級)の統計をかせぐためにビンを荒くするような前処理は不要です。例として,100倍に薄めて0のビンも多数含むようにしたデータをフィットしてみても,うまくいきます:
sp100 = numeric(9900)
for (i in 1:99) {
sp100[(100*i-99):(100*i)] =
hist(sample(1:100, sp[i], replace=TRUE), plot=FALSE, breaks=0:100)$counts
}
data = data.frame(sp=sp100, ch=1:9900)
fit = glm(sp ~ ch + dnorm((ch-5000)/500), data=data,
family=poisson(link="identity"))
# あるいは
# fit = gnls(sp ~ c + d*ch + e*dnorm((ch-5000)/500), data=data,
# start=list(c=0.5,d=0,e=1), weights=varPower(fixed=0.5))
正解のわかっている意地悪な矩形ピークのフィットを比較してみましょう。
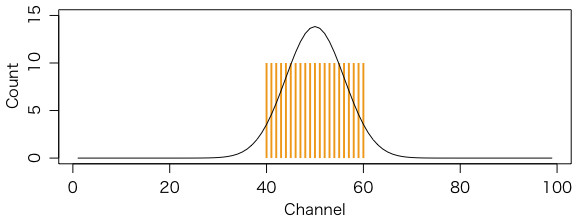
ch = 1:99 # チャンネル番号は1から99まで
sp = c(rep(0,39),rep(10,21),rep(0,39)) # 0が39,10が21,0が39
sum(sp) # 正解は210
plot(ch, sp, type="h", col="#f39800", lwd=2, lend=1, ylim=c(0,15),
xlab="Channel", ylab="Count") # 上の橙色のグラフ
fit = nls(sp ~ e*dnorm((ch-50)/s), start=list(e=10,s=5)) # 通常の最小2乗法
sum(fitted(fit)) # 222.9805 大きすぎる
fit = nls(sp ~ e*dnorm((ch-50)/s), start=list(e=10,s=5), weights=1/sp) # エラー
fit = nls(sp ~ e*dnorm((ch-50)/s), start=list(e=10,s=5), weights=1/(sp+1))
sum(fitted(fit)) # 171.9977 # 小さすぎる
library(nlme)
data = data.frame(ch=ch, sp=sp)
fit = gnls(sp ~ e*dnorm((ch-50)/s), data=data,
start=list(e=10,s=5),
weights=varPower(fixed=0.5),
control=list(nlsTol=1e-4))
sum(fitted(fit)) # 210 正解!
a = coef(fit)
a
# e s
# 34.680374 6.055298 # 係数
v = vcov(fit) # 共分散行列
sqrt(v['e','e']/a['e']^2 + v['s','s']/a['s']^2 + 2*v['e','s']/(a['e']*a['s']))
# e
# 0.05793257 # 相対誤差の推定値はやや小さめ
points(ch, fitted(fit), type="l")
fit = glm(sp ~ dnorm((ch-50)/5)-1, data=data, family=poisson(link="identity"))
sum(fitted(fit)) # 210 正解!
fit = glm(sp ~ dnorm((ch-50)/6)-1, data=data, family=poisson(link="identity"))
sum(fitted(fit)) # 210 正解!
fit = glm(sp ~ dnorm((ch-50)/7)-1, data=data, family=poisson(link="identity"))
sum(fitted(fit)) # 210 正解!
ご覧のように gnls() では正解ですが誤差の評価がやや甘くなっています。glm() は幅を指定する必要がありますが,指定した幅にかかわらず正解になり,しかも誤差(summary(fit)
で出る)も正解(210-1/2)です。
ポアソン分布を仮定した最尤法によるフィッティングでは,なぜ総カウント数が保存されるのでしょうか。
ポアソン分布のところでも述べたように,
\[ p_k = \frac{\lambda^k e^{-\lambda}}{k!} \]がポアソン分布です。ピークフィットでは各チャンネルのカウント数がポアソン分布でチャンネルごとに独立と仮定するので,確率は積
\[ \prod \frac{{\lambda_i}^{k_i} e^{-\lambda_i}}{k_i!} \]になります。各チャンネルの観測されたカウント数 $k_i$ を定数と見なしたときの上の式の値(尤度)を最大にする $\lambda_i$ を求めるのが最尤法ですが,計算しやすいように,尤度の対数から定数を省略したもの
\[ \sum (k_i \log \lambda_i - \lambda_i) \]を最大にします。また,$\lambda_i$ はチャンネルごとに自由に選べるのではなく,少数のパラメータで特徴づけられる滑らかな曲線です。代表的なパラメータを $x$ とすると,尤度最大の点ではそのパラメータについての導関数が 0 となるはずですので,
\[ \sum \lambda_i'(x) \left( \frac{k_i}{\lambda_i(x)} - 1 \right) = 0 \]となります。特に $x$ が曲線全体の高さを決めるパラメータであるならば,$\lambda_i(x) = a_i x$ と置けば,尤度最大の点では
\[ \sum a_i x = \sum k_i \]となります。つまり,この条件を満たしながら他のパラメータを調節して対数尤度が最小になるようにすればいいわけです。
Last modified: