コベル法と正規分布のフィットとが違う値を与える実際のデータに似せて作った人工データで,和田先生にいただいたものです。
ch = 1:99
sp = c(15081,15341,15281,15102,14989,15204,14943,15081,15036,
14970,14697,14649,14696,14448,14828,14896,14623,14508,14488,
14564,14558,14324,14553,14458,14535,14620,14408,14786,14579,
14581,14719,14984,14906,15200,15630,15806,16155,17268,18343,
19748,21421,24265,27189,31730,37736,46385,57310,71672,90530,
101320,99321,82894,61463,41234,27954,20644,17013,14990,13944,
13374,13150,12970,12790,12660,12921,12572,12483,12532,12434,
12626,12511,12492,12378,12602,12556,12406,12262,12297,12252,
12201,12079,12059,12073,11794,12224,12085,11996,12048,12097,
12137,12108,12079,11830,11934,11885,11902,11874,11721,11694)
plot(ch, sp, type="l", col="#f39800",
xlab="Channel", ylab="Count", ylim=range(c(0,sp)))
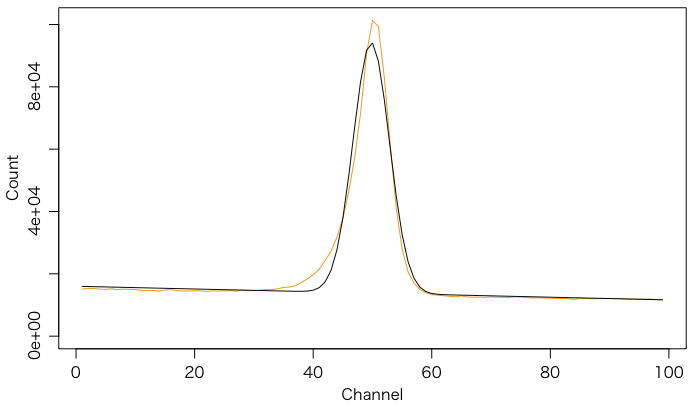
次の図のオレンジの線がデータで,黒い線が下の方法でフィットしたものです。

フィットは直線+正規分布で,R の nlme パッケージの gnls()
を使いました。モデルとデータが合っていないので,初期値をうまく選ばないと収束しません。初期値の正規分布の幅を実際より広くとるのがコツのようです。
library(nlme)
data = data.frame(ch=ch, sp=sp)
fit = gnls(sp ~ c + d*ch + e*dnorm((ch-m)/s), data=data,
start=list(c=15000,d=-40,e=200000,m=50,s=5),
weights=varPower(fixed=0.5))
points(fitted(fit), type="l")
a = coef(fit) # 係数
# a
# c d e m s
# 16013.281391 -43.917180 201684.467385 49.790450 3.067981
sum(a['e']*dnorm((data$ch-a['m'])/a['s']))
# [1] 618764.2
v = vcov(fit) # 共分散行列
sqrt(v['e','e']/a['e']^2 + v['s','s']/a['s']^2 + 2*v['e','s']/(a['e']*a['s']))
# e
# 0.02231194
0.02454814 * 618764.2 # 誤差
# [1] 15189.51
つまり 618764.2 ± 15189.5 がピークカウントです。
念のためピークの位置と幅が与えられたとして glm()
関数を使ってポアソン回帰をしてみます:
fit2 = glm(sp ~ ch + dnorm((ch-a['m'])/a['s']), data=data,
family=poisson(link="identity"))
summary(fit2)$coefficients[3,1:2]*sum(dnorm((ch-a['m'])/a['s']))
# Estimate Std. Error
# 618764.1946 915.6401
こちらでは 618764.2 ± 915.6 となりました。
一方,コベル法で,ピークをチャンネル30〜60として,バックグラウンドは両側から20点ずつとってやってみると,
sum(sp[30:60]) - (31/40)*(sum(sp[10:29])+sum(sp[61:80]))
# [1] 658684.7
sqrt(sum(sp[30:60]) + (31/40)^2*(sum(sp[10:29])+sum(sp[61:80])))
# [1] 1185.765
つまり 658684.7 ± 1185.8 となり,正規分布によるピークフィットよりやや大きな値になります。
gnls() や glm() を使った正規分布によるフィットは,全体ではデータをうまく再現しています:
> sum(fitted(fit)) # フィットの積分
[1] 1986689
> sum(sp) # データの積分
[1] 1986689
しかし,グラフを詳しく見ればわかるように,本当のバックグラウンド(オレンジの線の周辺部分)よりも,フィットした値(黒の曲線)がやや上に来てしまっています。これは,ピークの左側の高い裾(指数分布的な部分)の影響で,バックグラウンドをやや過大評価してしまったために,つじつまを合わせるためにピークをやや過小評価することになったと考えられます。
Last modified: