だんだん長くなってきましたので,このページは主にコベル法を扱い,より高度なピークフィットは次のページに分けました。
コベル法(the Covell method)はスペクトルのピーク
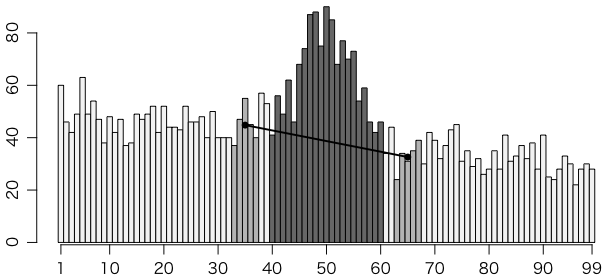
例えば次のような右下がりのバックグラウンド(背景)にピークが乗ったスペクトルがあったとしましょう。中央の40〜60がピークを含む領域(ROI,region of interest,関心領域)だとします。コベル法では,背景をROIの左右の適当な領域の平均値を結ぶ線分で近似します。ここではROIから2チャンネル置いた左右5チャンネルずつを使うことにしましょう。
この場合は,他のピークが見えませんので,バックグラウンドを定める領域はもっと広いほうがいいのですが(左右ともROIの幅の半分以上),ここでは5チャンネルずつしか使っていません。下のほうで別の方法と比べたりしていますが,バックグラウンドを定めるためのチャンネルの数が違うので,誤差の比較に意味はありません。

この図はRで次のようにして描きました。乱数ですので毎回結果が異なります。念のため今回の図を描いたときのデータをコメントで入れておきました。
## par(family="HiraKakuProN-W3") # Macの和文フォント指定
par(mgp=c(2,0.8,0)) # 好み(グラフの余白の調節)
bg = function(x) { 50 - 0.2 * x } # バックグラウンド
pe = function(x) { 100 * dnorm((x-50)/5) } # ピーク
ch = 1:99 # チャンネル(1,2,…,99)
sp = rpois(99, bg(ch)+pe(ch))
# sp = c(60,46,42,49,63,49,54,47,38,48,42,47,37,38,49,47,49,52,42,52,44,44,43,52,
# 46,46,48,40,50,40,40,40,37,47,55,45,40,57,53,41,56,49,62,46,68,74,87,88,75,
# 90,85,68,77,70,73,54,59,46,42,46,34,44,24,34,31,35,39,30,42,39,32,37,43,45,
# 31,35,29,32,26,28,35,28,41,31,33,37,32,38,28,41,25,24,28,33,30,22,28,30,28)
barplot(sp, space=0,
col=c(rep(gray(0.95),32),rep(gray(0.7),5),
rep(gray(0.95),2),rep(gray(0.4),21),
rep(gray(0.95),2),rep(gray(0.7),5),
rep(gray(0.95),32)))
points(c(35,65)-0.5, c(mean(sp[33:37]),mean(sp[63:67])),
type="o", pch=16, lwd=2)
t = c(1, seq(10,90,10), 99)
axis(1, t-0.5, t)
ROIの全体(gross)のカウントは
sum(sp[40:60])
ですが,これに対応するバックグラウンドをここでは左側の5チャンネル33〜37と右側の5チャンネル63〜67から決めます。この場合は21チャンネルのROIについて左右対称に10チャンネル分の領域を選びましたので,その平均の21倍(つまり10チャンネルの合計の2.1倍)がROIのバックグラウンドになります。全体からバックグラウンドを引いた正味(net)のカウントは次のようにして計算できます。
> sum(sp[40:60]) - 2.1 * sum(sp[c(33:37,63:67)])
[1] 543.3
この正味カウントの誤差は,次のように,係数を2乗して引き算を足し算にし,全体に平方根を付けて求めます。
> sqrt(sum(sp[40:60]) + 2.1^2 * sum(sp[c(33:37,63:67)]))
[1] 55.34139
つまり正味のカウント±誤差は 543±55 ということになります。
理由:ポアソン分布のところで説明したように,カウント値の分布はポアソン分布です。ポアソン分布をする確率変数 $X$ の分散(標準偏差の2乗)$V(X)$ は,$X$ の期待値 $E(X)$ に等しくなります。また,ポアソン分布に限らず,独立な二つの確率変数 $X$ と $Y$ があれば,その線形結合の分散 $V(aX + bY)$ は $a^2 V(X) + b^2 V(Y)$ に等しくなります。これで $V(X)$ を $E(X)$ で置き換え,さらに $E(X)$ を $X$ の計測値(カウント値)で近似して分散を求めます。その平方根が誤差になります。
このようにして誤差を求めるときは,必ず各チャンネルの実際のカウント値またはその合計を使います。カウント値の平均を使ったり,カウントの率(cpmやcps)を使ったりしてはいけません。その上で,計算に使った係数をすべて2乗して,引き算を足し算にし,全体の平方根を求めます。
コベル法は1959年に提案された非常に古い方法です(参考文献[1])。参考文献 [4] の5.4節にも “The Covell method was used in the early days of digital gamma-ray spectrometry …” と書かれています。コンピュータで重み付き最小二乗法でフィットして求めるのが現代的な方法です。しかし,考え方を理解するためや,図から人力で値や誤差を求めるには,便利な方法です。また,スペクトルのフィット:例4のようなデータとモデルが一致しない場合にもコベル法は頑健です。
コベル法の類は,グロス計数 $S$ とバックグラウンド計数 $B$ から,正味の計数 $S - kB$ とその誤差分散 $S + k^2 B$ を求める方法ですが,そのときの検出下限値は誤差の3倍(例えば)とするCooperの方法がシンプルでわかりやすく,文献 [2] でも推奨しています。このとき検出下限値は
\[ S - kB = 3\sqrt{S + k^2 B} \]を満たしますので,これを $N = S - kB$ について解いた
\[ N = \frac{1}{2}\left( \sqrt{36kB(1+k)+81} + 9 \right) \](上の例では約155)に対応する物理量が検出下限値になります。
コベル法で求めたカウントの誤差の程度を推定するために,簡単なシミュレーションをしてみましょう。
bg = function(x) { 50 - 0.2 * x }
pe = function(x) { 100 * dnorm((x-50)/5) }
foo = function() {
sp = rpois(99, bg(ch)+pe(ch))
sum(sp[40:60]) - 2.1 * sum(sp[c(33:37,63:67)])
}
r = replicate(100000, foo()) # 100000回繰り返す
mean(r) # 470程度
sd(r) # 56程度
想定した答えは sum(pe(ch)) つまり500ですので,上のコベル法の領域の取り方ではピークを少し過小評価しているようです。
Last modified: