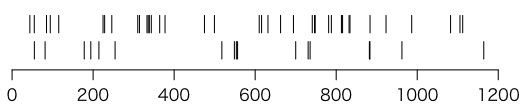
次の図は1200秒間に初代ポケットガイガー(PINフォトダイオードを使った放射線計)が放射線をカウントした時刻を示したものです。下は机の上にそのまま置いた場合(全部で17カウント),上はやさしお(カリウムを多く含む塩)の上に置いた場合(全部で38カウント)です。

par(mgp=c(2,0.8,0))
plot(c(0,1200), c(0,3), type="n", axes=FALSE, xlab="", ylab="")
axis(1)
x1 = c(55,81.5,178.1,194.4,214.3,254.3,517.8,548.7,
553.6,556.6,700.1,730.7,735.6,881.9,883.3,962.2,1164.2)
x2 = c(43.9,54.8,85,94.3,115.2,224.5,228.5,246.1,310.2,
314.4,333,336,338.8,343.7,364.3,377.6,474.8,499.5,
610,615.8,631.6,662.7,694.5,740.9,746.5,748.1,781.4,
788.1,812.9,815.7,831.7,834.1,883.5,923,986.4,1082.3,1105.5,1112.2)
segments(x1, 0.5, x1, 1.5)
segments(x2, 2, x2, 3)
次の図は0以上1200以下の一様乱数です。下は17個,上は38個発生させました。

plot(c(0,1200), c(0,3), type="n", axes=FALSE, xlab="", ylab="")
axis(1)
r1 = runif(17) * 1200
r2 = runif(38) * 1200
segments(r1, 0.5, r1, 1.5)
segments(r2, 2, r2, 3)
このように,ランダムに事象が発生するということは,決して一定の時間間隔で起きるのではなく,すぐ続いて起きたり,しばらく起きなかったりします。
以下では,このようなランダムに起こる事象を扱います。
問:やさしおの上に置いたときのほうが,そうでないとき(バックグラウンド)と比べてカウントが多いといえるでしょうか。
ここをクリックすると答えが現れるかもしれません。
ポケットガイガーを第4世代iPod touchにつないだときの感度は閾値13%で12.210cpm/μSv/hとされています(cpm = counts per minute)。つまり1分間のカウント数を12.21で割ればμSv/h単位になります。20分で17回は 17/20/12.21 で約0.07μSv/hに,20分で38回は 38/20/12.21 で約0.16μSv/hになります。
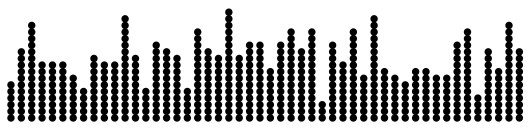
仮に毎分平均10回カウントするとして,毎分のカウント数をシミュレーションで描いてみましょう。全部で50分として,500カウントを用意し,それをランダムに50個の「ビン」に投げ込むと考えます:
stripchart(sample(1:50, 500, replace=TRUE),
pch=16, method="stack", axes=FALSE, at=0)
このように,毎分平均10回でも,20回近く起こることもあれば,3回しか起こらないこともあります。これが以下で説明するポアソン分布です。
1時間(あるいは1日あるいは1月あるいは1年あるいは…)に平均して $\lambda$ 回「でたらめに」起こる事象が,1時間(あるいは…)にちょうど $k$ 回起きる確率は,
\[ p_k = \frac{\lambda^k e^{-\lambda}}{k!} \]です(証明はあとで)。このような分布をポアソン分布(Poisson distribution)といいます。
もうちょっと詳しく言うと,1時間(あるいは1日あるいは…)を $n$ 等分し,個々の細かい時間間隔に事象が起きる確率が $p$ であるとします。すると,元の1時間(あるいは…)に事象が起きる回数の期待値は $\lambda = np$ です。ここで $\lambda$ を一定に保ちながら $n \to \infty$,$p \to 0$ の極限を考えます。このときの1時間(あるいは…)あたりの事象の起こる回数の分布がポアソン分布です。
よくポアソン分布は「珍しい(ほとんど起きない)」事象の分布だと言われることがありますが,おそらくこの $p \to 0$ から「珍しい」という言葉が出たのだと思います。同時に $n \to \infty$ をしますので,両者の積である $\lambda$ は必ずしも小さくなく,「珍しい」というのは当たりません。1時間に百回起こっても千回起こってもポアソン分布はポアソン分布です。
ポアソン分布では,平均と分散が等しくなるということが最重要です。
証明:ポアソン分布は2項分布で生起確率 $p \to 0$ の極限を取ればいい。2項分布の平均は $np$,分散は $np(1-p)$ なので $p \to 0$ なら $1-p \to 1$ だから,ポアソン分布は平均も分散も $np$ である。
2項分布の平均が $np$,分散が $np(1-p)$ の証明:表が出る確率が $p$ の1枚の硬貨を投げて表の出る枚数を数えるともちろん 0 か 1 だが,その枚数の平均は当然 $p$ になる。分散は $p(1-p)^2 + (1-p)p^2 = p(1-p)(1-p+p) = p(1-p)$ である。これは1枚の場合なので,$n$ 枚なら平均は $np$,分散は $np(1-p)$ になる。
この節の最初に出てきたポアソン分布の式は,2項分布
\[ p_k = \frac{n!}{k!(n-k)!} p^k (1-p)^{n-k} \]の極限として導けます。
\[ np = \lambda, \quad p \to 0, \quad n \to \infty \]とすると
\[ p_k = \frac{n(n-1)(n-2)\cdots(n-k+1) \cdot p^k}{k!} \frac{(1-p)^n}{(1-p)^k} = \frac{(np)^k}{k!} ((1-p)^{1/p})^{\lambda} = \frac{\lambda^k e^{-\lambda}}{k!} \]となります。
ポアソン分布で事象が次々に起こる様子をポアソン過程といいます。ポアソン過程で,ある事象が起きてから次の事象が起きるまでの時間を $t$ とすると,$n$ 等分した細かい時間間隔 $nt$ 個で事象が起こらないわけですから,その確率は $(1-p)^{nt} = ((1-p)^{1/p})^{\lambda t} \to e^{-\lambda t}$ に比例する指数分布になります。$t$ について 0 から $\infty$ まで積分して1になるように比例定数を決めると密度関数は $\lambda e^{-\lambda t}$ になります。事象間の時間間隔の平均は $1/\lambda$ です。ポアソン過程は,窓口に来る客,交通事故,放射線のカウントなど,いろいろな事象をモデル化するのに使われています。
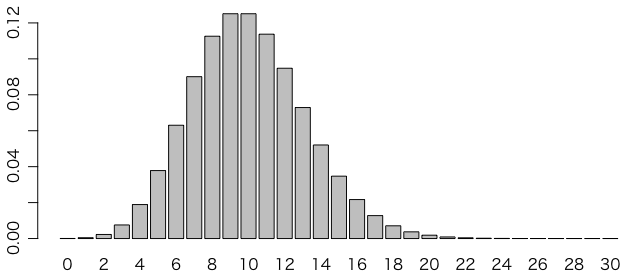
次のグラフは,$\lambda = 10$ のポアソン分布の確率分布を $k \leqq 30$ について表したものです($k > 30$ の確率はゼロではありませんが無視できる程度です)。
このグラフを描くためのRのコード:
par(mgp=c(2,0.8,0))
barplot(dpois(0:30,10), names.arg=0:30)
ご覧のように,平均10回起こる事象がぴったり10回起こる確率は約0.125に過ぎません。ぴったり9回起こる確率も約0.125です。ぴったり11回起こる確率は約0.114,というふうに,かなり広がりがあります。
「1μSv/hで100cpm」のガイガーカウンタの場合,0.1μSv/hでは毎分平均10回カウントします。しかしこれは平均で,実際には4回しかカウントしないことも16回カウントすることもある,というのが上の図でわかります。
ちなみに,ガイガーカウンタは,放射線をカウントしてから次にカウントできるまでに,ほんの少し時間が必要です(つまり不感時間があります)。このため厳密にはポアソンではありませんが,通常の線量ではポアソンで近似できます。
平均 $\lambda$ のポアソン分布は,分散も $\lambda$ になります。つまり標準偏差は $\sqrt{\lambda}$ になります。上のグラフのポアソン分布の場合,$\lambda = 10$ ですから,標準偏差は10の平方根の3.16ほどです。正規分布で近似すると,±標準偏差の範囲に収まる確率はほぼ68%ですから,68%の確率で10±3つまり7から13の範囲に入るといえます。実際にポアソン分布の確率を足し算してみると
sum(10^(7:13) * exp(-10) / factorial(7:13))
で約73%になります。同じ計算は
ppois(13,10) - ppois(6,10)
でもできます。
上のような荒い意味で,1単位時間に $\lambda$ 回事象が起きたとき,その誤差は $\sqrt{\lambda}$ であるという言い方をすることがあります。しかしこれを文字通りに受け取ると,1単位時間に 0 回事象が起きたとき,誤差は 0 であると誤解してしまいがちです。
実際,放射線の測定でカウントが 0 であった場合に,誤差も 0 であると記した例がありました。これは間違いです。

もっとも,この「測定値 0」はバックグラウンドを引いた後の値が検出限界未満(ND)であることを意味しているはずで,カウントが 0 という意味ではありません。
回数0の場合も含めて誤差を理解するためには「信頼区間」という考え方が必要になります。
統計学では「95%信頼区間」を考えることが多いのですが,物理の測定では「(統計)誤差」といえば正規分布の $\pm \sigma$ に相当するもの(68%信頼区間)を指すことが多いと思います。先に「95%信頼区間」を説明しましょう。
正規分布で $\pm \sigma$ の範囲内に入る確率は
1 - 2 * pnorm(-1)
で計算でき,0.6826895 になります。以下では 0.6826895 のことを「68%」と書いています。
物理の測定誤差には統計誤差(statistical error)のほか系統誤差(systematic error)がありますが,ここでは統計誤差だけを考えています。
一定時間にある事象が10回観測されたとしましょう。詳しい説明は後にして,Rに
poisson.test(10)
と打ち込んでみましょう。次のように出力されるはずです:
Exact Poisson test
data: 10 time base: 1
number of events = 10, time base = 1, p-value = 1.114e-07
alternative hypothesis: true event rate is not equal to 1
95 percent confidence interval:
4.795389 18.390356
sample estimates:
event rate
10
この「95 percent confidence interval」というところに注目してください。これは,ポアソン分布を仮定したとき,$\lambda$ の95%信頼区間が約 4.8 以上 18.4 以下であることを示しています(報告する際にはよく $[4.8, 18.4]$ のように書きます)。
95%信頼区間の意味は,仮に分布が $\lambda = 18.4$ のポアソン分布であれば,10回またはそれより少ない回数しか起こらない確率は2.5%だということと,仮に分布が $\lambda = 4.8$ のポアソン分布であれば,10回またはそれより多い回数起こる確率が2.5%だということを意味します。つまり,
ppois(10, 18.390356)
と打てば0.025と返り,
ppois(9, 4.795389)
と打てば0.975と返ります。ppois($q$,$\lambda$) は平均 $\lambda$ のポアソン分布で $q$ 回またはそれより少ない回数しか起こらない確率を出力する関数です。
統計的検定のことばでいえば,$\lambda = 18.4$ のポアソン分布であるという帰無仮説についての片側 $p$ 値が2.5%であり,$\lambda = 4.8$ のポアソン分布であるという帰無仮説についての片側 $p$ 値が2.5%であるという意味です。
同様に,一定時間にある事象が10回観測されたなら,$\lambda$ の68%信頼区間は 6.9 から 14.3 の範囲です。これは
poisson.test(10, conf.level=0.6826895)
と打ち込むと出力されます。この意味は,仮に $\lambda$ が 14.3 であれば10回またはそれより少ない回数しか起こらない確率は16% (=(100%-68%)/2)で,仮に $\lambda$ が 6.9 であれば10回またはそれより多い回数起こる確率が16%だということです。実際,
ppois(10, 14.266950)
と打てば0.1586552と返り,
ppois(9, 6.891306)
と打てば 0.8413447 (= 1 - 0.1586553) と返ります。
実際に起きた回数 $n$ が大きければ,$\lambda$ の68%信頼区間は $n \pm \sqrt{n}$ で近似できますが,$n$ が小さい場合はそうなりません。例えば0回しか起きなかった場合,68%信頼区間は $\pm 0$ ではなく,
poisson.test(0, conf.level=0.6826895)
と打てばわかるように 0 から 1.841022 までとなります。実際,
ppois(0, 1.841022)
と打てば 0.1586552 が返ります。
同様に,0回しか起きない場合の $\lambda$ の95%信頼区間は $[0, 3.7]$ です。また,正規分布の $\pm 3\sigma$ に相当する99.73%信頼区間は $[0, 6.6]$ です。これらの意味づけはいろいろ考えられますが,例えば,今まで50年間に一度も日本で原子力発電所の事故が起きなかったとしても,事故が起きる確率は0ではなく,50年に3.7回とか6.6回とか起きる状態であるかもしれないのです。
一度も起きたことのないことは通常の統計学では扱えないという人がいますが,ちゃんと扱えていますよね。
poisson.test(0, conf.level=0.9) と打つと,90%信頼区間(片側95%信頼区間)は $[0, 2.996]$ となり,その上限はほぼ3です。つまり,何も起こらなくても3回くらい起こる可能性は十分あるということで,このことを rule of three というようです(たいした法則ではないですね)。
このrule of threeを使えば,例えば1000回に1回しか起こらない現象を95%の確率で観測するには3000回観測しなければならないことや,1万人に1人の割合で副作用のある薬で副作用を発見するには3万人に投与しなければならないことがわかります。
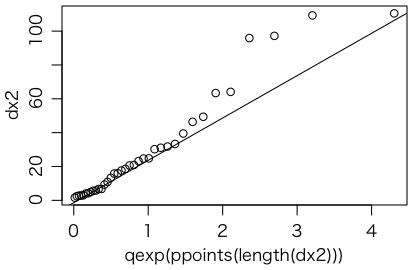
このページの最初のRコードの x1 や x2 のような列がポアソン過程かどうか調べるには,差分をとって qqplot() で指数分布かどうか調べるのがよいでしょう。
dx2 = diff(x2)
qqplot(qexp(ppoints(length(dx2))), dx2)
qqline(dx2, distribution=function(p){qexp(p)})
やや外れているように見えますが,乱数 r2 = runif(38) * 1200 でもこれくらいの外れはよく起きますので,ポアソン過程と見なしてよいでしょう。
これが $\lambda = 38/1200$ の指数分布(密度関数 $\lambda e^{-\lambda t}$)であるといえるかをコルモゴロフ・スミルノフ検定(Kolmogorov-Smirnov test)で調べるには次のようにします:
ks.test(dx2, "pexp", 38/1200, exact=TRUE)
$p = 0.6$ 程度で,指数分布でないとはいえません。
鉛の容器にある試料を入れて放射線を計測したところ,カウント数は $n$ でした。同じ条件で何も入れないで計測したところ,カウント数は 0 でした。$n$ がいくつ以上であれば放射性物質が含まれると考えてよいでしょうか。
上本道久「検出限界と定量下限の考え方」(『ぶんせき』2010年5月号pp.216-221,日本分析化学会,PDF[上本道久『分析化学における測定値の正しい取り扱い方』(日刊工業新聞社,2011年)にもほぼ同様のことが詳しく説明されています])によれば,「約 99.7% の確かさでもってバックグラウンド(ブランク)の信号分布に被測定物質が検出されないと言える最低量(平均値 + $3\sigma$)が検出限界として定義されていると考えるとよい」とのことです。また,「定量下限」という概念もあり,こちらは定義はよりあいまいですが $10\sigma$ 程度のようです。ここでは $3\sigma$(両側 $p$ 値 0.27%)をもって「検出された」とすることにします。
測定値 $n$ だけでなく,バックグラウンド 0 も,誤差を含む測定値(あるポアソン分布をする確率変数の値)です。一般にポアソン分布の差(Skellam分布といいます。Rにskellamというパッケージがあります)を考えるのはたいへんややこしいのですが,ここで考える場合は非常に簡単です。
skellamパッケージはCRANから削除されたようです(アーカイブは残っています)。VGAMパッケージにも dskellam(),rskellam(),skellam() という関数があります。
バックグラウンドも試料も同じ条件で計測したのですから,放射線のカウントがランダムだとすれば,個々のカウントがバックグラウンドに行く確率も試料に行く確率も同じです。これは2項分布ですが,両側 $p$ 値が 0.27% ということは片側で 1/1000 強,つまり $1/2^{10}$ 強ですので,$n = 10$ ならこの $p$ 値より小さくなります。つまりバックグラウンドが 0 なら少なくとも 10 カウントなければ検出されたと見なさない(ND = Not Detected)というわけです。
これはバックグラウンドのカウントの実測値が 0 であった場合です。バックグラウンドが完全に 0 であることがわかっている場合は,たとえ試料の実測値が 1 であっても,試料の真値が 0 であるという帰無仮説は完全に否定されます(ND になりません)。
別の例を考えましょう。バックグラウンドのカウントが 100 ありました。試料のカウントがどれだけあれば検出したと見なすべきでしょうか。
binom.test(100, 249, 0.5)
と打てば $p$ 値が 0.002285 で,0.27% より小さくなりますので,全部で249カウント,つまり試料が149カウントすればいいことになります。
Kendall's Advanced Theory of Statistics, 6th ed. Vol.2A の p.235,21.21に同様な問題があります。
これだけカウントが多ければ正規分布で近似できます。ポアソン分布の分散はカウント数に等しいのでそれぞれ100と149で,差の分散は分散の和ですので249です。標準偏差 $\sigma$ はこの平方根15.78で,$3\sigma = 47.3$ ほどですので,100と149では $3\sigma$ 以上の隔たりがあり,「検出した」と言えます。正規分布近似では100と148でも「検出」になり,正確な計算では100と148ではNDになるという違いがありますが,無視できるほどの違いです。
実際にバックグラウンド100に対して149や148といった値が出た場合は,「49±16」あるいは「ND (< 49)」に相当する実際の値(単位はBq/kgとか)を報告することになるでしょう。
ここでの計算は統計誤差しか考えていません。現実にはほかの誤差も入ってきます。今はそちらのほう(機械がカリウムのコンプトン散乱やビスマスをセシウムと間違えたり,不慣れな人が機械を操作したりすることも含めて)が深刻な問題になっています。
Last modified: