やさしおはNaCl(塩化ナトリウム:通常の塩)の半分をKCl(塩化カリウム)で置き換えたものです。100g中では27.6gがカリウムです。
カリウム(元素記号K,英語ではpotassium)の大部分は安定な 39K ですが,放射性の 40K も約0.0117%だけ含まれています。この 40K は半減期 1.251×109 年(12.51億年)で壊変し,89.1%は1.311MeVのβ線を出し,10.7%は1.461MeVのγ線を出します(数値はすべて『アイソトープ手帳』11版によりました)。
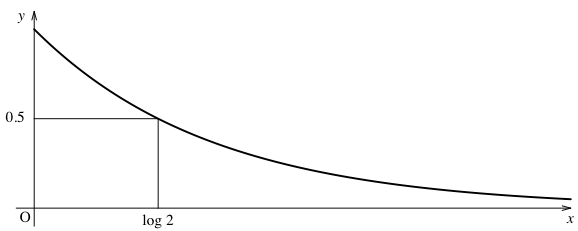
半減期とは物質が半分になるまでの時間です。放射性物質は指数関数 $y = e^{-x}$ のグラフのように減っていきます。この横軸を時間と考えて,$\log 2$ となっているところを 40K では12.51億年に読み替えます。

念のため,この図を描いたRのプログラムです(やや手抜き)。
par(family="serif")
par(xpd=NA)
curve(exp(-x), xlim=c(0,3), ylim=c(0,1.1),
axes=FALSE, xlab="", ylab="", lwd=2, asp=1)
arrows(-0.1, 0, 3, 0, length=0.1, angle=15)
arrows(0, -0.1, 0, 1.1, length=0.1, angle=15)
text(3, 0, expression(italic(x)), pos=1)
text(0, 1.05, expression(italic(y)), pos=2)
text(-0.05, -0.05, "O")
segments(0, 0.5, log(2), 0.5)
segments(log(2), 0.5, log(2), 0)
text(0, 0.5, "0.5", pos=2)
text(log(2), 0, "log 2", pos=1)
秒数を $t$ とすれば,壊変によって物質が減っていく様子は
\[ y = \exp \left( -\frac{t \log 2}{1.251 \times 10^9 \times 365.2422 \times 24 \times 60 \times 60} \right) \]のように表せますので,$t = 0$ における減少率は,これを微分して
\[ \left. \frac{dy}{dt} \right|_{t=0} = -\frac{\log 2}{1.251 \times 10^9 \times 365.2422 \times 24 \times 60 \times 60} \]となります。
やさしお1kgには276gのカリウムが含まれ,この0.0117%が 40K であるということは,1kg中に0.032292gの 40K が含まれることになります。40K は約40gが1モルですから,0.032292gでは0.0008073モルになり,アボガドロ数 6.022×1023 を掛ければ 4.86×1020 個になります。これに上の減少率を掛ければ毎秒約8500回の壊変が起こることになります。つまり約8500Bq/kgです:
> 276 * 0.000117/40 * 6.022e23 * log(2) / (1.251e9 * 365.2422 * 24 * 60 * 60)
[1] 8535.897
人間の体にも1人あたり6000Bqほどの放射性物質が含まれています(うち4000Bqほどが 40K)が,まったく心配する必要はありません。
Last modified: