ブートストラップ

ブートストラップとは

ブートストラップ（bootstrap）は統計学者Efronが(考案した|流行らせた)計算方法です。

コンピュータによるシミュレーションの一種ですが，データを乱数で生成するのではなく，実際のデータに基づいた推論ができるのが，ブートストラップの特徴です。

例えば平均値と中央値（メジアン）のどちらが安定か（ぶれが少ないか）を調べるために，通常のシミュレーションでは「乱数でデータを生成して平均値と中央値を計算する」という作業を何度も繰り返し，その分布を比較します。これに対して，ブートストラップでは，「実際のデータ（n 個）からランダムに n 個を復元抽出（重複を許した抽出）し，その平均値と中央値を計算する」という作業を何度も繰り返します。例えば実際のデータが (2, 3, 5, 7) であれば，それから復元抽出した (2, 3, 3, 7), (3, 5, 7, 7), (2, 5, 5, 5) などについて統計量（平均値，中央値など）を計算し，その分布を調べます。

この驚くほど単純な方法で，従来は正規分布など数学的に理想化された分布についてしか求めることができなかった統計量の分布（例えば中央値の分布）を，現実のデータとほぼ同じ分布について求めることができるのです。

ブートストラップについてはたくさんの本が出ていますが，考案者Efronと弟子のTibshiraniが書いた入門書 An Introduction to the Bootstrap (1993) がわかりやすいと思います。三重大学の図書館にもあります。

ライブラリを使わない簡単な例

ブートストラップ用のライブラリを使わない簡単な例です。

データとしては，あまり意味がありませんが，昔の鳩山内閣の資産データが私のブログ 閣僚資産：平均かメジアンか にありますので，これを使って，閣僚本人の資産の平均値や中央値の標本誤差を求めてみましょう（これは標本ではないので標本誤差を求めることは無意味です。あくまでも練習のため）。

念のためここにも書いておきます（2009-10-24各紙報道，単位：万円）：

名,本人,家族含む
鳩山由紀夫首相,144269,144269
菅直人副総理兼国家戦略担当相,905,2232
原口一博総務相,914,1220
千葉景子法相,3523,3523
岡田克也外相,3273,8641
藤井裕久財務相,14356,20214
川端達夫文部科学相,4024,5583
長妻昭厚生労働相,0,891
赤松広隆農相,4864,5934
直嶋正行経済産業相,3333,3333
前原誠司国土交通相,741,1441
小沢鋭仁環境相,2089,4014
北沢俊美防衛相,309,609
平野博文官房長官,1195,1875
中井洽国家公安委員長,1296,1296
亀井静香金融・郵政担当相,9427,18745
福島瑞穂消費者・少子化担当相,12734,25000
仙谷由人行政刷新担当相,1968,3987

これを shisan.csv というファイルに保存して読み込みます：

X = read.csv("shisan.csv")

本人の資産のサマリーを調べます：

> summary(X$本人)
    Min.  1st Qu.   Median     Mean  3rd Qu.     Max. 
     0.0    984.2   2681.0  11620.0   4654.0 144300.0

平均値1億1620万円，中央値2681万円です。これらの標本誤差を求めるために，1000個のブートストラップ標本を生成して，その平均値・中央値の分布を調べましょう。中央値なら

md = replicate(1000, median(sample(X$本人, 18, replace=TRUE)))

でできます。これは次のループと同じことです：

md = numeric(1000)
for (i in 1:1000) {
  md[i] = median(sample(X$本人, 18, replace=TRUE))
}

同様に平均値も mn に求めて比較してみます：

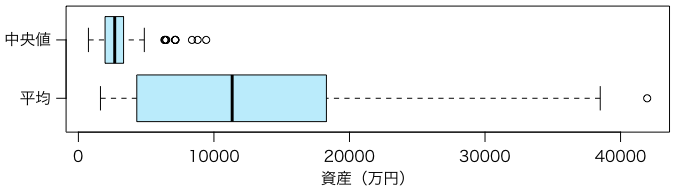
boxplot(mn, md, col="#b4ebfa", names=c("平均", "中央値"),
        horizontal=TRUE, las=TRUE, xlab="資産（万円）")

このデータの場合，中央値のほうが小さく，ばらつき（標本誤差）も小さいことがわかります。

ライブラリboot

Rのブートストラップ用ライブラリとしては，上で紹介した入門書 An Introduction to the Bootstrap に基づいた bootstrap や，DavisonとHinkleyの Bootstrap Methods and Their Applications (1997) に基づいた boot があります。後者がより一般的です。

> library(boot)
> b = boot(X, function(d,k) median(d$本人[k]), R=100000)
> b

ORDINARY NONPARAMETRIC BOOTSTRAP


Call:
boot(data = X, statistic = function(d, k) median(d$本人[k]), 
    R = 1e+05)


Bootstrap Statistics :
    original    bias    std. error
t1*     2681 -32.10432    1005.341

この2行目 b = ... は，次のように分けて書くほうがわかりやすいかもしれません：

foo = function(d, k) {
  median(d$本人[k])
}
b = boot(X, foo, R=100000)

boot() の第1引数は全データを含むベクトルまたは行列またはデータフレームで，第2引数で与える関数の第1引数に引き継がれます。第2引数で与える関数は統計量を求めるためのもので，その第2引数はデータの行インデックスです（ライブラリを使わない例で sample(18,replace=TRUE) を入れたものです）。引数 R=... がブートストラップ・サンプルの数です。boot() の第2引数で与えた関数はR回呼び出されます。Rは通常1000回あれば十分です。

最初の original = 2681 が元のサンプルについての統計量（ここでは中央値）で，これはブートストラップとは関係せず単に median(X$本人) を求めたものです。

次の bias = -32.10432 は，中央値の期待値が中央値の真の値からどれだけ外れているかをブートストラップで推測したものです。こんなに有効桁数があるわけではありませんが，中央値の期待値が真の中央値より数十程度小さい可能性があることを示しています。具体的には，ブートストラップによる統計量の平均値から，元のサンプルの統計量を引いたものです。ここでは，このバイアスの値は，次に述べる標準誤差より十分小さいので，無視することができますが，そうでない場合は統計量に問題があるのかもしれません。

最後の std. error が中央値の標準誤差（standard error）をブートストラップで推定したもので，中央値はサンプルごとにこれくらいの標準偏差のばらつきがあることを示しています。具体的には，ブートストラップによる統計量の標準偏差（n - 1 で割る方式）を求めているだけです。

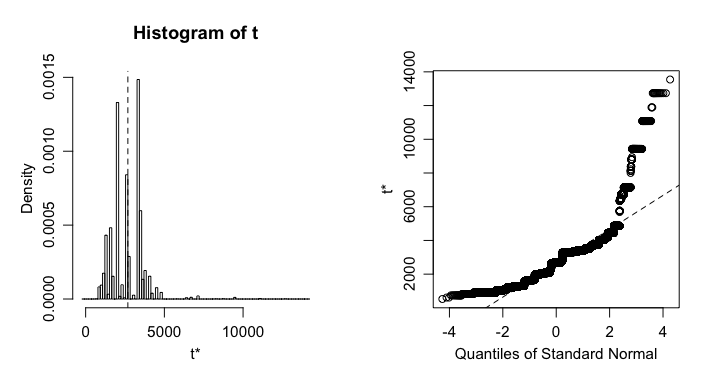
結果を変数（ここでは b）に入れておくと，後でより詳しい結果を出力することができます。例えば plot(b) とすればブートストラップされた統計量の分布がプロットされます。

par(mgp=c(2,0.8,0))
plot(b)
ブートストラップのプロット

Last modified: