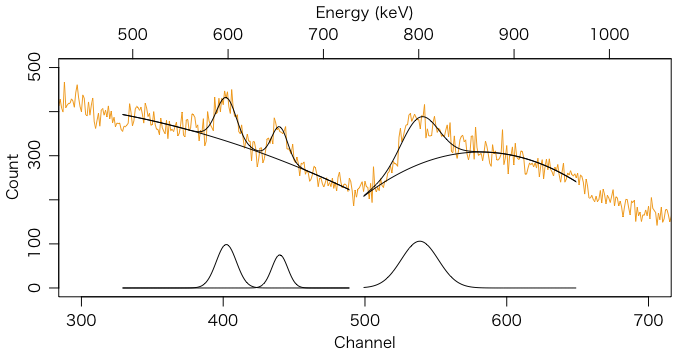
mikageさんの 放射線スペクトル表示ツール SPViewer のページからリンクされている テクノAP TS100B-15 スペクトル公開 の [TS100B-15] 日光産しいたけスペクトル(10時間) をフィットしてみます。まずはRでデータを読み込み,図を描きます。チャンネル番号の1.4872倍がエネルギー(keV)であることがわかっているので,グラフの上にエネルギー目盛を描きました。
# quartz() # MacでX11を使わない場合
# par(family="HiraKakuProN-W3") # Mac:フォント(好み)
# par(mgp=c(2,0.8,0)) # 好み
data = read.csv("http://dl.dropbox.com/u/52911779/spviewer/ts100_nikkoushiitake.csv",
skip=13)
names(data) = c("ch","sp")
attach(data) # これでdata$ch等は単にch等と書ける
plot(ch, sp, type="l", xlab="Channel", ylab="Count", col="#f39800", xlim=c(300,700), ylim=c(0,500))
t = pretty(1.4872*c(300,700))
axis(3, t/1.4872, t)
mtext("Energy (keV)", 3, 2)

三つある山は 134Cs の605keV(97.6%)と796keV(85.5%)および 137Cs の662keV(85.1%)と考えられます。ここではバックグラウンドを無理に一つの関数で表さず,左半分と右半分で別々の2次関数でフィットすることにします。上に凸な放物線になりますので,直線を使うよりピークカウントは少なめになるはずです。
library(nlme)
rng1 = 330:490
fit1 = gnls(sp ~ c + d*(ch-400) + b*(ch-400)^2
+ e1*dnorm((ch-m1)/s1)
+ e2*dnorm((ch-m2)/s2),
data=data, subset=rng1,
start=list(c=300,d=-1,b=0,e1=200,e2=200,
m1=605/1.4872,m2=662/1.4872,s1=7,s2=7),
weights=varPower(fixed=0.5),
control=list(nlsTol=1e-4,returnObject=TRUE))
points(ch[rng1], fitted(fit1), type="l")
rng2 = 500:650
fit2 = gnls(sp ~ c + d*(ch-550) + b*(ch-550)^2
+ e3*dnorm((ch-m3)/s3),
data=data, subset=rng2,
start=list(c=300,d=1,b=0,e3=200,
m3=796/1.4872,s3=10),
weights=varPower(fixed=0.5),
control=list(nlsTol=1e-4,returnObject=TRUE))
points(ch[rng2], fitted(fit2), type="l")
a1 = coef(fit1)
a2 = coef(fit2)
points(ch[rng1], a1['c']+a1['d']*(ch[rng1]-400)+a1['b']*(ch[rng1]-400)^2, type="l")
points(ch[rng1], a1['e1']*dnorm((ch[rng1]-a1['m1'])/a1['s1']), type="l")
points(ch[rng1], a1['e2']*dnorm((ch[rng1]-a1['m2'])/a1['s2']), type="l")
points(ch[rng2], a2['c']+a2['d']*(ch[rng2]-550)+a2['b']*(ch[rng2]-550)^2, type="l")
points(ch[rng2], a2['e3']*dnorm((ch[rng2]-a2['m3'])/a2['s3']), type="l")
バックグラウンドを除いた正規分布曲線の下の面積とその誤差の推定値は次のようにして求められます。
# 各山のカウント
> sum(a1['e1']*dnorm((ch-a1['m1'])/a1['s1']))
[1] 1754.059
> sum(a1['e2']*dnorm((ch-a1['m2'])/a1['s2']))
[1] 1052.243
> sum(a2['e3']*dnorm((ch-a2['m3'])/a2['s3']))
[1] 3475.492
> v1 = vcov(fit1)
> v2 = vcov(fit2)
> # 各山の相対誤差
> sqrt(v1['e1','e1']/a1['e1']^2 + v1['s1','s1']/a1['s1']^2 + 2*v1['e1','s1']/(a1['e1']*a1['s1']))
e1
0.1071091
> sqrt(v1['e2','e2']/a1['e2']^2 + v1['s2','s2']/a1['s2']^2 + 2*v1['e2','s2']/(a1['e2']*a1['s2']))
e2
0.1327097
> sqrt(v2['e3','e3']/a2['e3']^2 + v2['s3','s3']/a2['s3']^2 + 2*v2['e3','s3']/(a2['e3']*a2['s3']))
e3
0.09845207
Last modified: