mikageさんの 放射線スペクトル表示ツール SPViewer のページのスペクトル例の FNF-401による牛乳のベクレル測定 をフィットしてみます。まずはRでデータを読み込み,図を描きます。
# quartz() # MacでX11を使わない場合
# par(family="HiraKakuProN-W3") # Mac:フォント(好み)
# par(mgp=c(2,0.8,0)) # 好み
data = read.csv("http://www.mikage.to/radiation/spviewer/data_fnf401/fnf401_milk.csv",
skip=22, nrow=1022, header=FALSE)
names(data) = c("ch","sp")
plot(data$ch, data$sp, type="l", xlab="Channel", ylab="Count", col="#f39800")
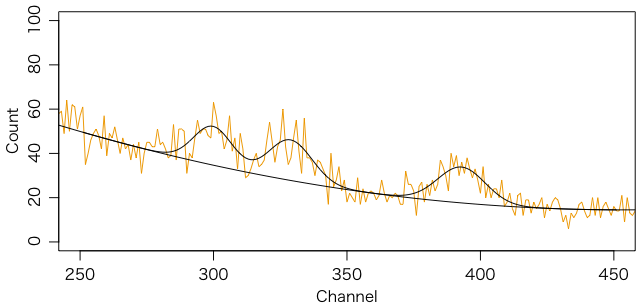
もっと細かいところを見てみます。
plot(data$ch, data$sp, type="l", xlim=c(250,450), ylim=c(0,100),
xlab="Channel", ylab="Count", col="#f39800")
以下でフィットした結果を最初に図に示しておきます。

三つある山は 134Cs の605keV(97.6%)と796keV(85.5%)および 137Cs の662keV(85.1%)と考えられますので,独立な量は二つですが,効率曲線(検出効率のエネルギー依存性)がわからないので,三つの山のカウントを独立に調べることにします。実際には 214Bi の609keV(46.1%)がかぶっていることがよくあるので,注意が必要です。
バックグラウンドを2次関数でフィットし,初期値に注意して次のようにフィットしました。エネルギーの校正がしっかりできていて,ピーク幅(のエネルギー依存性)もわかっていれば,パラメータをさらに減らすことができ,より安定なフィットができるはずです。
library(nlme)
fit = gnls(sp ~ c + d*(ch-350) + b*(ch-350)^2
+ e1*dnorm((ch-m1)/s1)
+ e2*dnorm((ch-m2)/s2)
+ e3*dnorm((ch-m3)/s3),
data=data, subset=250:450,
start=list(c=10,d=-0.05,b=0.001,e1=10,e2=10,e3=10,
m1=300,m2=325,m3=395,s1=7,s2=7,s3=7),
weights=varPower(fixed=0.5),
control=list(nlsTol=1e-4)) # 収束しないときは1e-3に直す
フィットを図に重ね書きしてみます。
points(data$ch[250:450], fitted(fit), type="l")
a = coef(fit)
points(data$ch, a['c']+a['d']*(data$ch-350)+a['b']*(data$ch-350)^2, type="l")
バックグラウンドを除いた正規分布曲線の下の面積とその誤差の推定値は次のようにして求められます。
> sum(a['e1']*dnorm((data$ch-a['m1'])/a['s1']))
[1] 318.0564
> sum(a['e2']*dnorm((data$ch-a['m2'])/a['s2']))
[1] 373.5237
> sum(a['e3']*dnorm((data$ch-a['m3'])/a['s3']))
[1] 362.1288
> v = vcov(fit)
> sqrt(v['e1','e1']/a['e1']^2 + v['s1','s1']/a['s1']^2 + 2*v['e1','s1']/(a['e1']*a['s1']))
e1
0.1652257
> sqrt(v['e2','e2']/a['e2']^2 + v['s2','s2']/a['s2']^2 + 2*v['e2','s2']/(a['e2']*a['s2']))
e2
0.1532264
> sqrt(v['e3','e3']/a['e3']^2 + v['s3','s3']/a['s3']^2 + 2*v['e3','s3']/(a['e3']*a['s3']))
e3
0.1377409
つまり,三山のカウントは318,374,362で,それぞれ相対誤差(1σ相当)は17%,15%,14%です。
あてはまりの良さを表すカイ2乗の値は次のようになります。
> sum((sp[250:450]-fitted(fit))^2/fitted(fit))
[1] 5688277
念のため詳しいサマリーも付けておきます:
> summary(fit)
Generalized nonlinear least squares fit
Model: sp ~ c + d * (ch - 350) + b * (ch - 350)^2 + e1 * dnorm((ch - m1)/s1) + e2 * dnorm((ch - m2)/s2) + e3 * dnorm((ch - m3)/s3)
Data: data
Subset: 250:450
AIC BIC logLik
1250.624 1293.567 -612.3122
Variance function:
Structure: Power of variance covariate
Formula: ~fitted(.)
Parameter estimates:
power
0.5
Coefficients:
Value Std.Error t-value p-value
c 23.6557 0.980140 24.1350 0
d -0.1771 0.007916 -22.3750 0
b 0.0009 0.000156 5.4996 0
e1 43.8678 6.245681 7.0237 0
e2 45.9427 5.572561 8.2444 0
e3 40.6349 4.399548 9.2362 0
m1 299.7492 1.161450 258.0818 0
m2 328.8164 1.097385 299.6363 0
m3 392.8915 0.994195 395.1856 0
s1 7.2503 1.249353 5.8033 0
s2 8.1302 1.224012 6.6423 0
s3 8.9118 1.114554 7.9958 0
Correlation:
c d b e1 e2 e3 m1 m2 m3 s1 s2
d -0.056
b -0.811 -0.278
e1 -0.253 0.160 0.135
e2 -0.308 0.114 0.208 0.081
e3 -0.277 -0.074 0.237 0.059 0.077
m1 0.067 -0.113 0.009 -0.093 0.086 -0.011
m2 -0.118 0.001 0.095 -0.090 0.110 0.033 0.244
m3 0.176 -0.067 -0.175 -0.048 -0.058 -0.037 0.012 -0.020
s1 -0.115 0.251 -0.037 -0.462 0.170 0.013 0.114 0.348 -0.024
s2 -0.411 0.017 0.342 0.199 -0.381 0.114 -0.327 -0.193 -0.073 -0.307
s3 -0.506 -0.147 0.400 0.109 0.142 -0.310 -0.022 0.061 -0.101 0.030 0.207
Standardized residuals:
Min Q1 Med Q3 Max
-2.357315267 -0.700992481 -0.009263635 0.609370883 2.404427920
Residual standard error: 0.9741925
Degrees of freedom: 201 total; 189 residual
バックグラウンドの部分は上では2次式としましたが,ほかに
sp ~ c + d*ch^b + ...
とか
sp ~ c + d/(ch-b) + ...
とか
sp ~ c + d/ch + b/ch^2 + ...
のようなフィットのしかたもあります。
また,実は 134Cs にはほかに569keV(15.4%)という小さなピークがあり,605keV(97.6%)の左裾を引き上げる形になります。ピークの面積は605keVの 15.4/97.6 = 0.158 倍ですが,ピークの幅がエネルギーの平方根に比例するとすれば幅が sqrt(569/605) = 0.97 倍になり,逆にピークの高さは 15.4/97.6 * sqrt(605/569) = 0.163 倍になります(実際にはエネルギーが下がれば効率が上がるのでもう少し大きな値になります)。これを含めて考えれば,フィットのしかたは例えば
fit = gnls(sp ~ c + d/ch + b/ch^2
+ e1*0.163*dnorm((ch-0.941*m1)/(0.97*s1))
+ e1*dnorm((ch-m1)/s1)
+ e2*dnorm((ch-m2)/s2)
+ e3*dnorm((ch-m3)/s3),
data=data, subset=250:450,
start=list(c=10,d=1000,b=1000,e1=10,e2=10,e3=10,
m1=300,m2=325,m3=395,s1=7,s2=7,s3=7),
weights=varPower(fixed=0.5),
control=list(nlsTol=1e-4))
のようになります。グラフは次のようになります。
points(data$ch[250:450], fitted(fit), type="l")
a = coef(fit)
points(data$ch, a['c']+a['d']/data$ch+a['b']/data$ch^2, type="l")
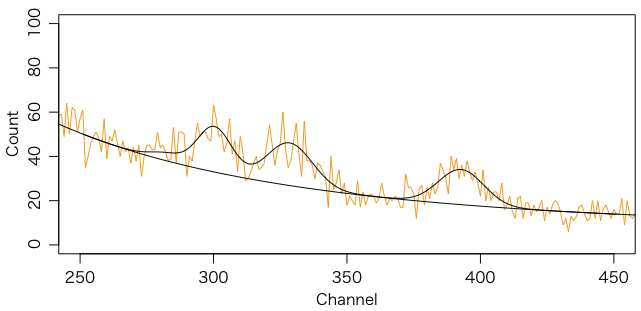
パラメータと各ピークのカウントは次のようになります。
> sum((sp[250:450]-fitted(fit))^2/fitted(fit))
[1] 5686931
> a
c d b e1 e2
1.407882e+01 -1.153124e+04 5.164312e+06 5.132408e+01 4.833267e+01
e3 m1 m2 m3 s1
3.983357e+01 3.002962e+02 3.285290e+02 3.927496e+02 6.466344e+00
s2 s3
8.594227e+00 8.479985e+00
> sum(a['e1']*dnorm((data$ch-a['m1'])/a['s1']))
[1] 331.8791
> sum(a['e2']*dnorm((data$ch-a['m2'])/a['s2']))
[1] 415.3819
> sum(a['e3']*dnorm((data$ch-a['m3'])/a['s3']))
[1] 337.7881
> v = vcov(fit)
> sqrt(v['e1','e1']/a['e1']^2 + v['s1','s1']/a['s1']^2 + 2*v['e1','s1']/(a['e1']*a['s1']))
e1
0.1427363
> sqrt(v['e2','e2']/a['e2']^2 + v['s2','s2']/a['s2']^2 + 2*v['e2','s2']/(a['e2']*a['s2']))
e2
0.1530434
> sqrt(v['e3','e3']/a['e3']^2 + v['s3','s3']/a['s3']^2 + 2*v['e3','s3']/(a['e3']*a['s3']))
e3
0.1331488
IAEAの文書を放医研が訳した原子力あるいは放射線緊急事態におけるモニタリングの一般的手順(PDF)のp.148に効率曲線の例が載っています。3×3インチNaIのfull energy peak efficiencyが900keVで0.03,300keVで0.06と読み取ると,全エネルギーピーク効率はエネルギーの約-0.63乗で減ることになります。これと85.5/97.6の分岐比とから (796/605)^(-0.63)*(85.5/97.6) のように計算すると,796keVのピークは605keVのピークの0.737倍の面積になると予想されます。
さらに,ピークの幅はエネルギーの平方根に比例すると仮定し,137Cs のエネルギー662keVが 134Cs の605keVと796keVを 0.298:0.702 に内分することを使えば,パラメータの数はさらに減らせます:
fit = gnls(sp ~ c + d/ch + b/ch^2
+ e1*0.169*dnorm((ch-0.941*m1)/(sqrt(0.941*m1)*r))
+ e1*dnorm((ch-m1)/(sqrt(m1)*r))
+ e2*dnorm((ch-(0.702*m1+0.298*m3))/(sqrt(0.702*m1+0.298*m3)*r))
+ e1*0.737*sqrt(m1/m3)*dnorm((ch-m3)/(sqrt(m3)*r)),
data=data, subset=250:450,
start=list(c=0,d=0,b=4000000,e1=50,e2=50,
m1=300,m3=393,r=0.4),
weights=varPower(fixed=0.5),
control=list(nlsTol=1e-4))
フィット曲線は一つ上とほぼ同じですので省略します。
ほかに考えられる効果としては,134Cs の796keVのコンプトン端がちょうど605keV付近にあります。2*796^2/(511+2*796) で計算すれば602.6keVになります。ここを境として,エネルギーの低い側が高くなるはずですので,1-pnorm((ch-0.996*m1)/(sqrt(0.996*m1)*r)) に比例する項をバックグラウンドに含めることが考えられます。
放射線量等分布マップのところでも書きましたが,放出された 134Cs と 137Cs の比は,2011年3月の時点まで遡れば,ベクレル(Bq)単位でほぼ1:1であることが知られています。福島原発由来のものであれば,この比とつじつまが合うようなフィットが望ましいのですが,それについてはまた後日書く予定です。
Last modified: