放射線量等分布マップ

はじめに

文科省の放射線量等分布マップの作成等に係る検討会（第7回）配付資料のページに資料第7-1号：土壌の核種分析結果（セシウム134、137）について（PDF:315KB）というデータが掲載されました。これはPDFファイルですが，CSV（Excelで開けるようにSJIS・CRLF）にした1310688_1.csvを置いておきます。ここではこれをRで解析してみます。

なお，@nnistar さんのつぶやき（これ，これ）によれば，以下の9点は怪しいかもしれません： 008S048, 008N024, 010N028, 030S042, 068N028, 070N028, 072N028, 072N030, 076N034

Rで読み込む

Rで次のように打ち込んでデータを data というオブジェクトに読み込みます。

data = read.csv("http://okumuralab.org/~okumura/stat/data/1310688_1.csv",
                as.is=TRUE, fileEncoding="SJIS", na.strings="-")

ここで as.is=TRUE は文字列をそのまま文字列として扱う指定です（Rのデフォルトではカテゴリーデータとして扱われます）。na.strings="-" はハイフンを欠測値（NA = Not Available）として扱うという指定です。欠測値として扱うべき文字列が複数ある場合は na.strings=c("","-","--") といった具合に指定します。CSVでは空文字列を欠測値とすることが多いようですが，PDFからデータを抜き出す際には何か入っていないと列がうまく認識できません（ちなみにセルの結合とセル内改行もPDFからデータを抜き出す際の大敵です）。Rは標準では欠測値を NA という文字列で表しますが，ハイフンのほうが一般にわかりやすいでしょう。

summary(data)

と打てばデータの要約が表示されます。この場合は13変数2180ケースの多変量データです。ここで数値なのに文字列として扱われた列がないか確かめます。

実は最初，欠測値があることに気づかず na.strings="-" を指定しなかったので，空間線量率が文字列になってしまいました。正規表現を使えば数字と小数点以外のデータを列挙できます：

data$空間線量率μSv_h[grep("[^0-9.]", data$空間線量率μSv_h)]

セシウム137とセシウム134の比

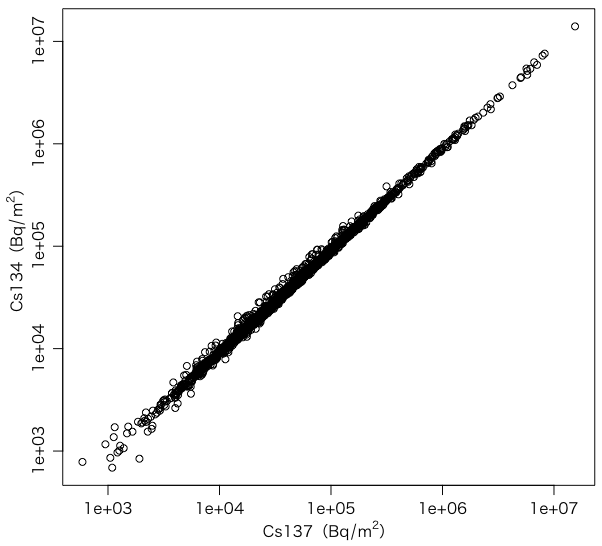
Cs137とCs134の放射能の面密度（Bq/m²）を比べてみましょう。Macでしか必要のないものは頭に # を付けてコメントアウトしてあります。

# quartz()  # MacでX11とQuartzを選べる環境の場合はQuartzのほうが高品位
# par(family="HiraKakuProN-W3") # Macでのフォント指定
par(mgp=c(2,0.8,0)) # 特に不要だがマージンの微調整
plot(data$Cs137_Bq_m2, data$Cs134_Bq_m2,
     xlab="Cs137（Bq/m2）", ylab="Cs134（Bq/m2）")

ここで m2 をちゃんと m² にしたければ少し工夫を要します：

plot(data$Cs137_Bq_m2, data$Cs134_Bq_m2,
     xlab=expression(paste("Cs137（", Bq/m^2, "）")),
     ylab=expression(paste("Cs134（", Bq/m^2, "）")))

さらにx軸もy軸も対数にします：

plot(data$Cs137_Bq_m2, data$Cs134_Bq_m2,
     xlab=expression(paste("Cs137（", Bq/m^2, "）")),
     ylab=expression(paste("Cs134（", Bq/m^2, "）")),
     log="xy")

もっと比をわかりやすくするためには次のようにするとよいでしょう。

plot(data$Cs137_Bq_m2+data$Cs134_Bq_m2,
     data$Cs134_Bq_m2/data$Cs137_Bq_m2,
     xlab=expression(paste("Cs134+Cs137（", Bq/m^2, "）")),
     ylab="Cs134/Cs137", log="x")

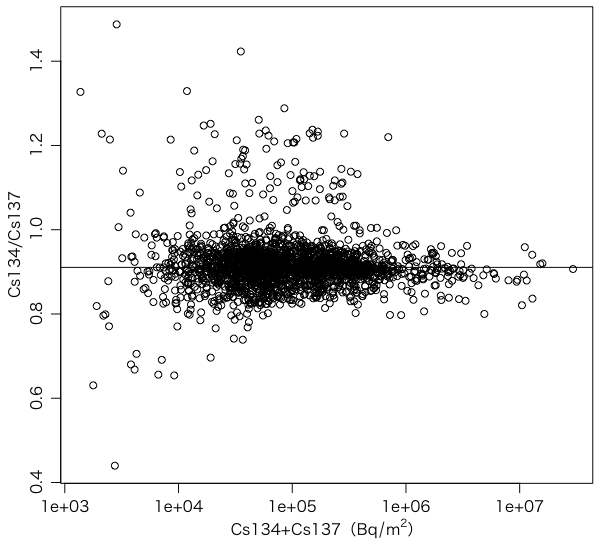
値が小さいほどばらつきが大きそうです。ちなみに，この図にはCs134/Cs137のメディアンの線が入れてあります。メディアンは

median(data$Cs134_Bq_m2/data$Cs137_Bq_m2)

で計算できます（0.91ほどです）。メディアンに合わせた横線を引くには次のようにします。

abline(h=median(data$Cs134_Bq_m2/data$Cs137_Bq_m2))

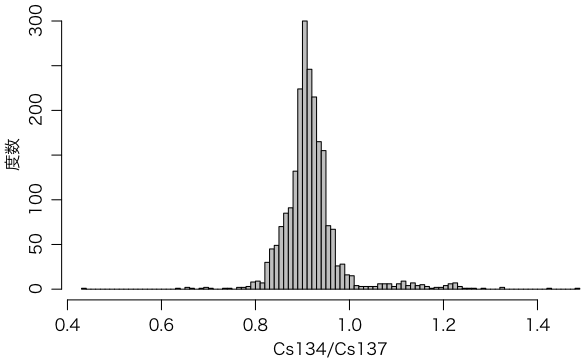
ついでにヒストグラムも描いてみます。breaks はおよその階級数です。階級の右端を含まない方式にするために right=FALSE というオプションを入れています（デフォルトでは逆）。

hist(data$Cs134_Bq_m2/data$Cs137_Bq_m2, breaks=100, right=FALSE,
     col="gray", xlab="Cs134/Cs137", ylab="度数", main="")

距離との関係

福島第一原発の位置は経度141.032339，緯度37.422778です。これをベクトルで表しておきます：

fuku1 = c(141.032339, 37.422778)

各点の経度・緯度を2180行2列の行列で表します：

p = cbind(data$経度_10進, data$緯度_10進)

このとき，各点と福島第一原発との距離は，空間データ（spatial data）を扱うためのspというパッケージで定義されている spDistsN1() という関数で求めます。spがインストールされていない場合は例えば次のようにしてインストールしておきます：

options(repos="http://cran.ism.ac.jp") # ダウンロード先（例：統数研）
install.packages("sp")

こうしてから次のようにして距離を求めます（単位：km）：

library(sp)
fuku1dist = spDistsN1(p, fuku1, longlat=TRUE)

この距離を横軸，Cs134/Cs137の比の値を縦軸にとって，プロットします：

plot(fuku1dist,
     data$Cs134_Bq_m2/data$Cs137_Bq_m2,
     xlab="福島第一原発との距離（km）",
     ylab="Cs134/Cs137")

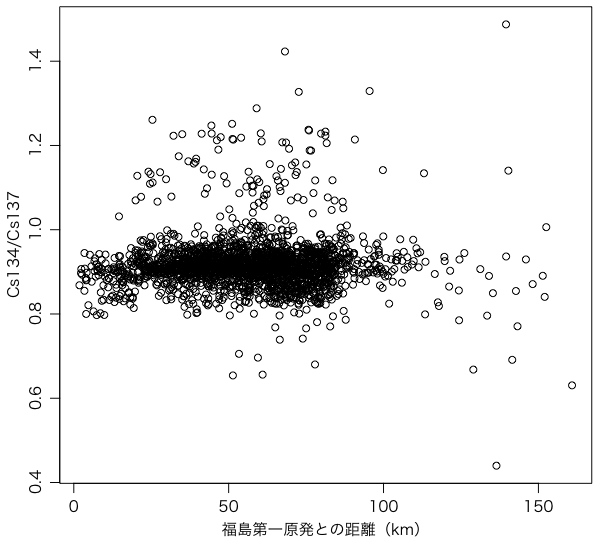
Cs134/Cs137 vs distance from Fukushima Daiichi

距離が大きいほどばらつきが大きいようにも見えますが，距離が大きいと値も小さいので，直接的な関係ではないのかもしれません。

地図に描く

Cs134/Cs137比が何によるのかをもっと詳しく調べるため，地図に描いてみることにします。使うのはRgoogleMapsというRのパッケージです。ついでにRColorBrewerも入れておきます。

options(repos="http://cran.ism.ac.jp") # ダウンロード先（例：統数研）
install.packages("png")
install.packages("RgoogleMaps")
install.packages("RColorBrewer")

これらパッケージと福島の地図を読み込みます：

library(RgoogleMaps)
library(RColorBrewer)
source("http://okumuralab.org/~okumura/stat/data/GetMap.R") # バグフィックス
FukushimaMap = GetMap(c(37.38,140.2), destfile="fukushima.png",
                      zoom=9, sensor="false", hl="ja")

中心位置とズーム値は適当です。次に色を適当に定義して地図上にプロットします。

cols = brewer.pal(11, "RdBu")[11:1]
cols = c(cols, cols[11])
tmp = PlotOnStaticMap(FukushimaMap,
        lat=data$緯度_10進, lon=data$経度_10進, pch=16,
        col=cols[floor((data$Cs134_Bq_m2/data$Cs137_Bq_m2)*10+0.5)-3])
tmp = PlotOnStaticMap(FukushimaMap,
        lat=37.422778, lon=141.032339,
        pch="×", cex=2, add=TRUE) # 福島第一原発
legend(-300, -290, xjust=0, yjust=0,
       legend=paste("〜",(14:4)/10,sep=""),
       fill=cols[11:1], bg="white")

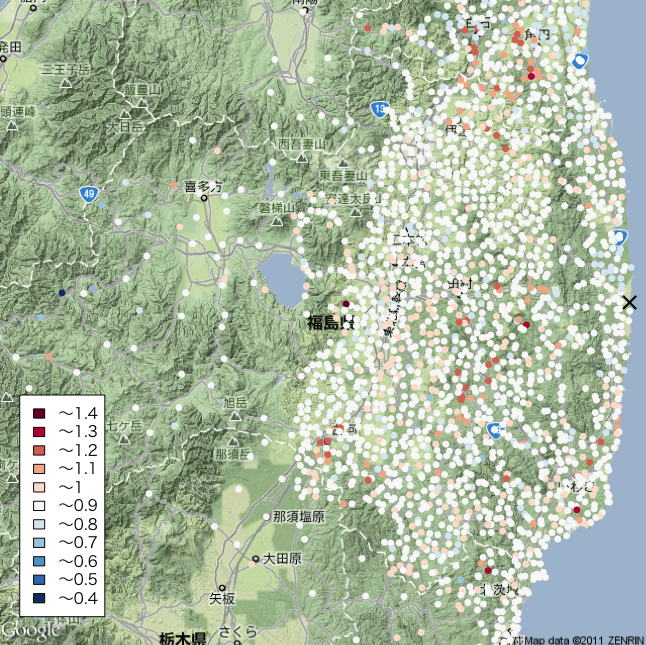
次は Cs134/Cs137 が 0.5 青白橙 1.5 で連続的に色を変えたものです。白が Cs134/Cs137 = 1 です。

cols = colorRamp(c("#004080","#0080ff","white","#ff8000","#804000"))
colfunc = function(x) { rgb(cols(pmin(pmax(x, 0), 1))/255) }
tmp = PlotOnStaticMap(FukushimaMap,
        lat=data$緯度_10進, lon=data$経度_10進, pch=16,
        col=colfunc(data$Cs134_Bq_m2/data$Cs137_Bq_m2 - 0.5))

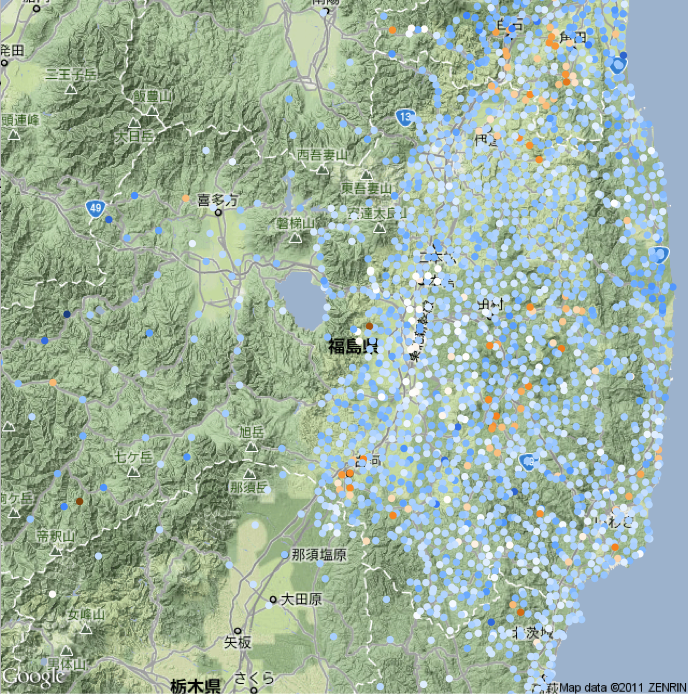
どちらも残念ながらあまりそれらしいパターンは見えてきません。

セシウムと空間線量率の関係

横軸にセシウムの総量，縦軸に空間線量率をとってプロットしてみます。

plot(data$Cs134_Bq_m2+data$Cs137_Bq_m2, data$空間線量率μSv_h,
     xlab=expression(paste("Cs134+Cs137（", Bq/m^2, "）")),
     ylab="空間線量率（μSv/h）")

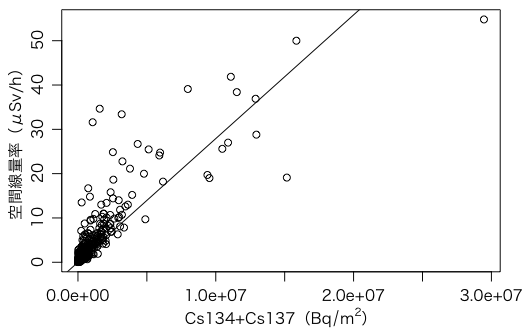
書き込んだ直線については，これから説明します。

空間線量率はセシウムの量の1次式で近似できるでしょうか。Rの lm() という関数で調べてみます。

lm(data$空間線量率μSv_h ~ data$Cs134_Bq_m2 + data$Cs137_Bq_m2)

結果は 7.794×10^-6Cs134 - 1.888×10^-6Cs137 + 4.643×10^-1 という変な式で，Cs137が増えると線量率は減ることになってしまいます。これは重回帰分析の常識で，説明変数間の相関が強い場合，つまり多重共線性（multicollinearity，「マルチコ」）のある場合には，重回帰分析の結果は不安定になります。実際，

model1 = lm(data$空間線量率μSv_h ~ data$Cs134_Bq_m2 + data$Cs137_Bq_m2)
summary(model1)

のようにして少し詳しい結果を出力してみれば，Cs137の係数は誤差が大きすぎて意味を持たないことがわかります。この場合，Cs134とCs137の単純和を使って，

cesium = data$Cs134_Bq_m2 + data$Cs137_Bq_m2
lm(data$空間線量率μSv_h ~ cesium)

あるいは定数項のないモデルを使って

lm(data$空間線量率μSv_h ~ cesium - 1)

とすれば，空間線量率は 2.792×10^-6(Cs134+Cs137) で予測できることがわかります。この直線をグラフに書き込むには

abline(0, 2.792e-6)

と打ち込みます。これが上の図でした。

ところで，本当はこういうグラフは両対数にするべきですね。

plot(cesium, data$空間線量率μSv_h,
     xlab=expression(paste("Cs134+Cs137（", Bq/m^2, "）")),
     ylab="空間線量率（μSv/h）", log="xy")

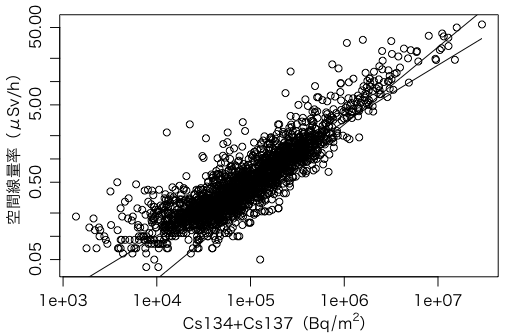
ここで2本の線を引きました。より急峻なものは先ほどの1次回帰で求めた線ですが，対数プロットでは必ずしも直線にならないので curve() という関数で描きます。

curve(2.792e-6 * x, add=TRUE)

水平に近いほうの線は

lm(log(data$空間線量率μSv_h) ~ log(cesium))

というモデルで求めたもので，

curve(exp(0.7353 * log(x) - 9.0598), add=TRUE)

で描きました。考察はお任せします。

3月11日時点に戻ると

以上は2011年9月3日に書いたことですが，炉が停止した 2011/3/11 時点でのCs134/Cs137比がTwitterで話題になり，遠藤知弘先生がいろいろ調べてくださいました。ここでも少し追記しておきます。上で考察したデータは 2011/6/14 時点に揃えたものですので，95日巻き戻せばいいわけです：

> t0 = as.POSIXct("2011/3/11")
> t1 = as.POSIXct("2011/6/14")
> t1-t0
Time difference of 95 days

まずCs134とCs137の半減期ですが，ここではBNLの Interactive Chart of Nuclides にあった値 2.0652，30.08 を使います：

yr = 95 / 365.2422
CsRatio = (data$Cs134_Bq_m2 * 2^(yr/2.0652)) / (data$Cs137_Bq_m2 * 2^(yr/30.08))
summary(CsRatio)
sd(CsRatio)

平均 0.9960，メディアン 0.9878，標準偏差 0.0734 であることがわかります。ついでに度数分布：

hist(CsRatio, breaks=100, right=FALSE, col="gray",
     xlab="Cs134/Cs137 as of 2011/3/11", ylab="度数", main="")
abline(v=1, col="red")

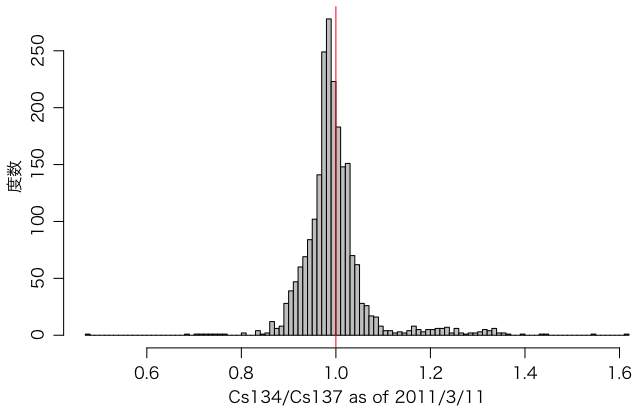
次は3月11日の Cs134/Cs137 が 0.5 青白橙 1.5 で連続的に色を変えたものです。白が Cs134/Cs137 = 1 です。

Cs134/Cs137の代表値は何が良いか（仮）

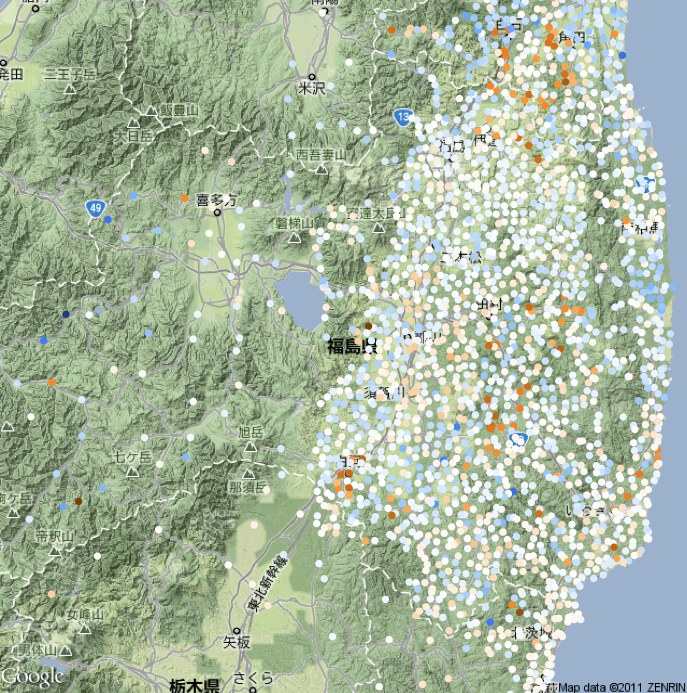
Cs134/Cs137比の代表値としては何を使えばいいでしょうか？

sum(Cs134) / sum(Cs137)
mean(Cs134 / Cs137)
median(Cs134 / Cs137)
exp(mean(log(Cs134 / Cs137)))

ほかにも重み付き平均や回帰係数などいろいろ考えられそうです。要は何を見たいかによるわけですが，ここでは，得られた値がどれだけ安定か（ぶれが少ないか）をブートストラップで調べてみました。

式	値	バイアス	標準誤差
sum(Cs134)/sum(Cs137)	0.9807	0.000043	0.0032
mean(Cs134/Cs137)	0.9960	0.000005	0.0016
median(Cs134/Cs137)	0.9878	0.000061	0.0009
exp(mean(log(Cs134/Cs137)))	0.9935	-0.000003	0.0015

library(boot)
yr = 95 / 365.2422
data311 = data.frame(Cs134=data$Cs134_Bq_m2 * 2^(yr/2.0652),
                     Cs137=data$Cs137_Bq_m2 * 2^(yr/30.08))
boot(data311, function(d,i) sum(d$Cs134[i])/sum(d$Cs137[i]), R=100000)
boot(data311, function(d,i) mean(d$Cs134[i]/d$Cs137[i]), R=100000)
boot(data311, function(d,i) median(d$Cs134[i]/d$Cs137[i]), R=100000)

ちなみに，mean(y/x) はあまり計算したくない量です。例えば

x = rnorm(1000000)+5
y = rnorm(1000000)+5
mean(y)/mean(x)
mean(y/x)
median(y/x)
exp(mean(log(y/x)))

などとしてみればわかるように，mean(y)/mean(x) や median(y/x) や相乗平均 exp(mean(log(y/x))) がほぼ 1 であるのに対して，mean(y/x) は 1 より大きくなりがちです。

奥村晴彦

Last modified: 2014-08-31 10:56:02