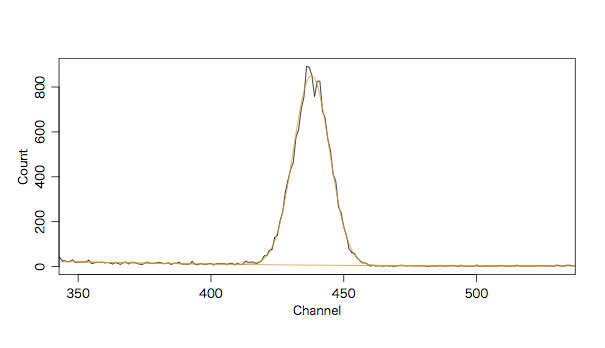
mikageさんの 放射線スペクトル表示ツール SPViewer のページのスペクトル例の TS-100によるCs-137線源スペクトル をフィットしてみます。まずはRでデータを読み込み,図を描きます。
# quartz() # MacでX11を使わない場合
# par(family="HiraKakuProN-W3") # Mac:フォント(好み)
# par(mgp=c(2,0.8,0)) # 好み
data = read.csv("http://www.mikage.to/radiation/spviewer/ts100_cs137.csv", skip=9)
plot(data$CH, data$COUNT, type="l", xlab="Channel", ylab="Count")
もっと細かいところを見てみます。
plot(data$CH, data$COUNT, type="l", xlim=c(350,530),
xlab="Channel", ylab="Count")
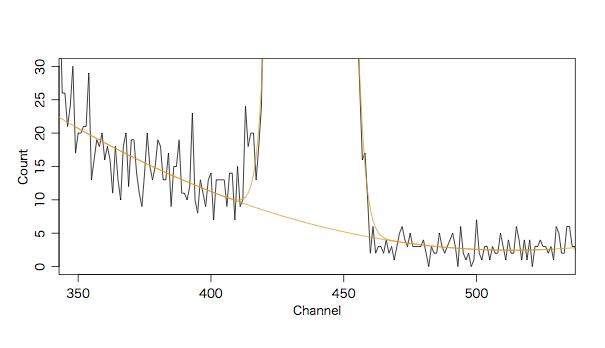
さらに下のほうを拡大します。
plot(data$CH, data$COUNT, type="l", xlim=c(350,530), ylim=c(0,30),
xlab="Channel", ylab="Count")


図を見ると,この範囲ではバックグラウンドは2次関数でフィットできそうなので,次のようにしました。
library(nlme)
res = gnls(COUNT ~ c + d*(CH-440) + b*(CH-440)^2 + e*dnorm((CH-m)/s),
data=data, subset=350:530,
start=list(c=5,d=-0.1,b=0.01,e=2000,m=440,s=20),
weights=varPower(fixed=0.5),
control=list(nlsTol=1e-4))
フィットを図に重ね書きしてみます。
points(data$CH[350:530], fitted(res), type="l", col="#f39800")
points(data$CH, a['c']+a['d']*(data$CH-440)+a['b']*(data$CH-440)^2,
type="l", col="#f39800")
バックグラウンドを除いた正規分布曲線の下の面積とその誤差の推定値は次のようにして求められます。
> a = coef(res)
> sum(a['e']*dnorm((data$CH-a['m'])/a['s']))
[1] 14416.28
> v = vcov(res)
> sqrt(v['e','e']/a['e']^2 + v['s','s']/a['s']^2 + 2*v['e','s']/(a['e']*a['s']))
e
0.009411989 # 1σ相当の相対誤差
つまり 14416(1±0.009) = 14416±136 ということになります。288秒の測定ですから,cps単位では 50.0±0.5 程度です。
念のため詳しいサマリーも付けておきます:
> summary(res)
Generalized nonlinear least squares fit
Model: COUNT ~ c + d * (CH - 440) + b * (CH - 440)^2 + e * dnorm((CH - m)/s)
Data: data
Subset: 350:530
AIC BIC logLik
1041.389 1063.778 -513.6943
Variance function:
Structure: Power of variance covariate
Formula: ~fitted(.)
Parameter estimates:
power
0.5
Coefficients:
Value Std.Error t-value p-value
c 6.1428 0.416939 14.733 0
d -0.1004 0.004747 -21.148 0
b 0.0007 0.000101 6.776 0
e 2120.9236 24.537439 86.436 0
m 437.8437 0.065010 6735.051 0
s 6.7972 0.050288 135.165 0
Correlation:
c d b e m
d -0.115
b -0.756 -0.368
e 0.038 -0.007 -0.025
m -0.007 -0.036 0.022 0.007
s -0.231 0.037 0.165 -0.584 0.002
Standardized residuals:
Min Q1 Med Q3 Max
-2.5557716 -0.6518855 -0.1365124 0.6014378 3.7578656
Residual standard error: 1.108315
Degrees of freedom: 181 total; 175 residual
Last modified: