皆様,宜しくお願い致します。
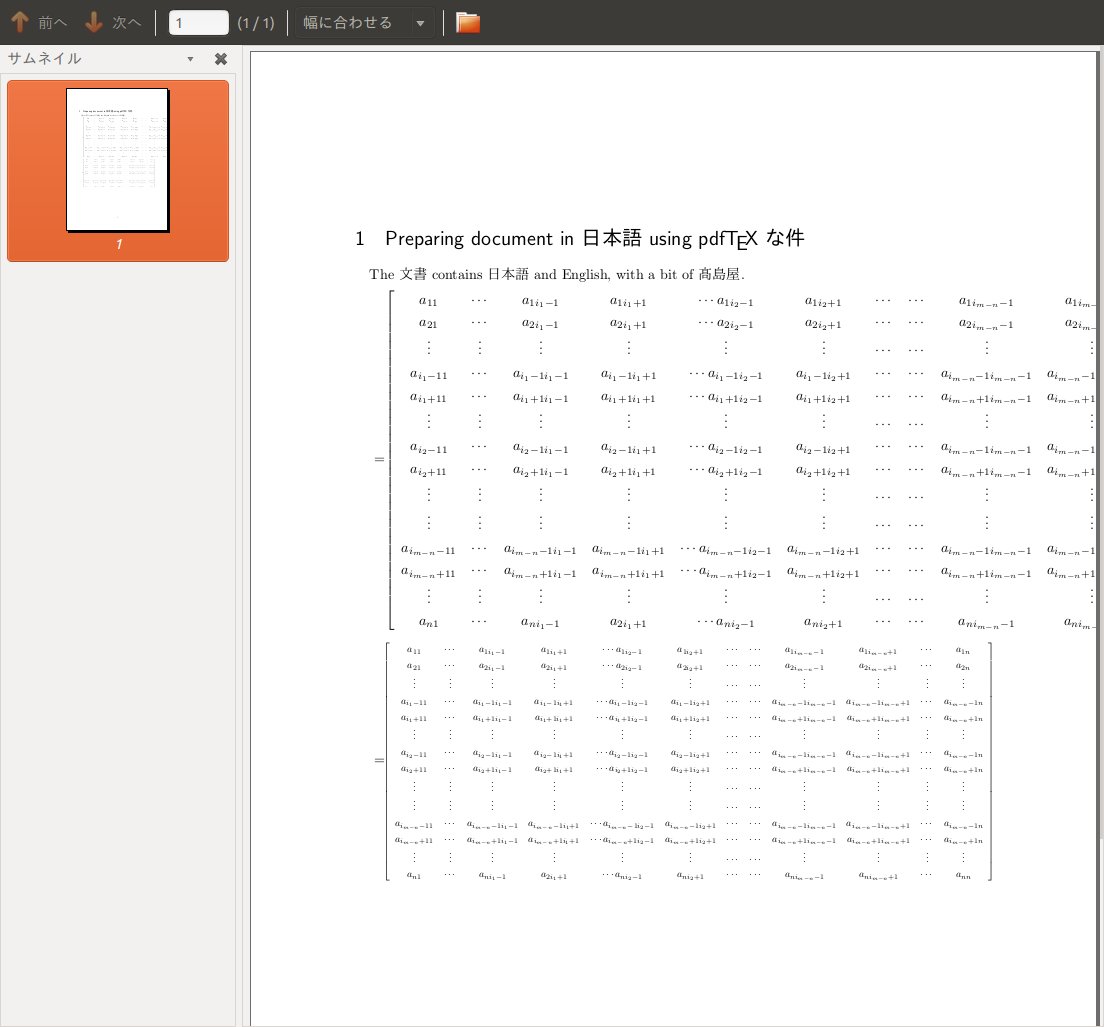
下記の行列を出力したら,行列の右側がはみ出してしまいました。
どうか行列を縮小する方法をお教え下さい。
$=\left[
\begin{array}{cccccccccccccc}
a_{11} & \cdots & a_{1i_1-1} & a_{1i_1+1} & \cdots a_{1i_2-1} & a_{1i_2+1} & \cdots & \cdots &a_{1i_{m-n}-1} & a_{1i_{m-n}+1} & \cdots & a_{1n} \\
a_{21} & \cdots & a_{2i_1-1} & a_{2i_1+1} & \cdots a_{2i_2-1} & a_{2i_2+1} & \cdots & \cdots &a_{2i_{m-n}-1} & a_{2i_{m-n}+1} & \cdots & a_{2n} \\
\vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \cdots & \cdots & \vdots & \vdots & \vdots & \vdots \\
a_{i_1-11} & \cdots & a_{i_1-1i_1-1} & a_{i_1-1i_1+1} & \cdots a_{i_1-1i_2-1} & a_{i_1-1i_2+1} & \cdots & \cdots &a_{i_{m-n}-1i_{m-n}-1} & a_{i_{m-n}-1i_{m-n}+1} & \cdots & a_{i_{m-n}-1n} \\
a_{i_1+11} & \cdots & a_{i_1+1i_1-1} & a_{i_1+1i_1+1} & \cdots a_{i_1+1i_2-1} & a_{i_1+1i_2+1} & \cdots & \cdots &a_{i_{m-n}+1i_{m-n}-1} & a_{i_{m-n}+1i_{m-n}+1} & \cdots & a_{i_{m-n}+1n} \\
\vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \cdots & \cdots & \vdots & \vdots & \vdots & \vdots \\
a_{i_2-11} & \cdots & a_{i_2-1i_1-1} & a_{i_2-1i_1+1} & \cdots a_{i_2-1i_2-1} & a_{i_2-1i_2+1} & \cdots & \cdots &a_{i_{m-n}-1i_{m-n}-1} & a_{i_{m-n}-1i_{m-n}+1} & \cdots & a_{i_{m-n}-1n} \\
a_{i_2+11} & \cdots & a_{i_2+1i_1-1} & a_{i_2+1i_1+1} & \cdots a_{i_2+1i_2-1} & a_{i_2+1i_2+1} & \cdots & \cdots &a_{i_{m-n}+1i_{m-n}-1} & a_{i_{m-n}+1i_{m-n}+1} & \cdots & a_{i_{m-n}+1n} \\
\vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \cdots & \cdots & \vdots & \vdots & \vdots & \vdots \\
\vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \cdots & \cdots & \vdots & \vdots & \vdots & \vdots \\
a_{i_{m-n}-11} & \cdots & a_{i_{m-n}-1i_1-1} & a_{i_{m-n}-1i_1+1} & \cdots a_{i_{m-n}-1i_2-1} & a_{i_{m-n}-1i_2+1} & \cdots & \cdots &a_{i_{m-n}-1i_{m-n}-1} & a_{i_{m-n}-1i_{m-n}+1} & \cdots & a_{i_{m-n}-1n} \\
a_{i_{m-n}+11} & \cdots & a_{i_{m-n}+1i_1-1} & a_{i_{m-n}+1i_1+1} & \cdots a_{i_{m-n}+1i_2-1} & a_{i_{m-n}+1i_2+1} & \cdots & \cdots &a_{i_{m-n}+1i_{m-n}-1} & a_{i_{m-n}+1i_{m-n}+1} & \cdots & a_{i_{m-n}+1n} \\
\vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \cdots & \cdots & \vdots & \vdots & \vdots & \vdots \\
a_{n1} & \cdots & a_{ni_1-1} & a_{2i_1+1} & \cdots a_{ni_2-1} & a_{ni_2+1} & \cdots & \cdots &a_{ni_{m-n}-1} & a_{ni_{m-n}+1} & \cdots & a_{nn}
\end{array}
\right]
$