$n$ 個の数値 $x_1$,$x_2$,...,$x_n$ が与えられたとき,これらの値を代表する値(代表値)として最もよく使われるのが平均値(mean,average)
\[ \bar{x} = \frac{x_1 + x_2 + \cdots + x_n}{n} \]です。$\bar{x}$(エックス・バー)は $x$ の平均値を意味します。
平均値を意味する英語は mean と average の二通りがあります。平均値を求めるのにExcelでは average() という関数を使いますが,Rでは短いほうの mean() が関数名になっています。
> x = c(0, 7, 8, 9, 100) > mean(x) [1] 24.8
上で定義したものを相加平均または算術平均(arithmetic mean)ともいいます。これに対して,積の $n$ 乗根
\[ \sqrt[n]{x_1 x_2 \cdots x_n} \]を相乗平均または幾何平均(geometric mean)といいます。これは
\[ \log \sqrt[n]{x_1 x_2 \cdots x_n} = \frac{\log x_1 + \log x_2 + \cdots + \log x_n}{n} \]と書けるので,$x \to \log x$ という変数変換をしたときの(相加)平均です。$x > 0$ の場合しか意味を持ちません。
運動競技などの採点で,極端な点数を付ける審査員の影響を少なくするために,点数を大きさの順に並べて,両側から同数ずつ削除してから平均を求めることがあります。このような平均を,トリム平均(トリムド平均),調整平均,刈り込み平均(trimmed mean)などと呼びます。Rでは mean() に trim=... というオプションを与えて計算します。次の例では20%ずつ両側から(合わせて約40%)外します(正確には,個数×0.2 を切り捨てて整数にした個数ずつ両側から外します)。
> mean(x, trim=0.2) [1] 8
このトリム平均を推し進めて,両側からどんどん外していき,残りが1個または2個になったときのトリム平均を,中央値またはメジアン(メディアン,median)といいます(学習指導要領では中学校1年の数学に「中央値」という用語が現れます)。つまり,$x_1 \leqq x_2 \leqq \cdots \leqq x_n$ となるように並べ替えて,$n$ が奇数なら $x_{(n+1)/2}$,$n$ が偶数なら $(x_{n/2} + x_{n/2+1}) / 2$ がメジアンです。Rでは median() という関数で求めます。
> median(x) [1] 8
これら三つの代表値の使い分けとしては,データの分布が後で説明する正規分布に近いなら平均値,後で説明するコーシー分布のように極端な値が非常に多いならメジアンのほうが安定した結果が得られます。トリム平均は,分布にかかわらず,最善ではないけれども妥当な代表値となるものとして,近年よく使われています。
ウィンザライズド平均(Winsorized mean)は,両側から同数を外すところまではトリム平均と同じですが,残ったものの最大値・最小値を両側に延ばしていって,元と同じ長さにします。例えば 0,7,8,9,100 の20%ウィンザライズド平均は 7,7,8,9,9 の平均になります。Winsorは人名です。
ミッドレンジ(midrange,範囲の中央)は,最大値と最小値の平均です。分布が一様分布なら,ミッドレンジが最も安定した代表値となります。
分布の形が左右非対称の場合,例えば所得(収入)の分布のような場合に,平均値を使うかメジアンを使うかで結果が大きく異なります。どちらが正しいということはなく,全員の収入をプールして均等に再分配したらどうなるかという意味では平均値ですし,「平均的な」人の収入という意味ではメジアンのほうが妥当です。
ネットで商品や作品の評価を投票できるサイトがたくさんあります。星一つ(★☆☆☆☆)から星五つ(★★★★★)までの5段階で評価するとき,星の数のどういう代表値を表示するのが妥当でしょうか。一般にどの代表値を使っているのでしょうか。調べてみましょう。
選挙で,似た政策を掲げる候補者が複数いると,共倒れすることがよくあります。例えば,2000年のアメリカ大統領選挙では,緑の党のラルフ・ネーダーが立候補したためにゴアの票が食われたのが,ブッシュ当選の一因と考えられます。このような現象をスポイラー効果(spoiler effect)といいます。スポイラー効果を防ぐために,一人にしか投票できない今の方式をやめて,複数の候補者に点数(または順位)を付けて投票できるようにしようという運動があります(例:Range Voting)。しかし,点数(または順位)の付け方や代表値の求め方が少しずつ違うたくさんの方式が提案され,まさに共倒れ現象で,従来の多数決投票方式を変えるに至っていません。詳しくは,ウィリアム・パウンドストーン『選挙のパラドクス―なぜあの人が選ばれるのか?』(青土社,2008年)をお読みください。
中央値は全体の50%の点です。同様に,0%の点(最小値),25%の点(第一四分位数),75%の点(第三四分位数),100%の点(最大値)もよく使われます。これらは quantile() という関数で求められます。例:
> quantile(1:10) 0% 25% 50% 75% 100% 1.00 3.25 5.50 7.75 10.00
ある変数 $X$ の値を調べようとすると,調べるたびに値が変わってしまうような,変な変数のことを,数学屋さんは確率変数(random variable)と呼び,コンピュータ屋さんは乱数(random numbers)と呼びます。確率変数は $X$ や $Y$ など大文字で表すことが多いようです。
上の定義はいいかげんです。以下ではさらに,毎回の値が独立(independent)であり,確率分布が同じ(identically distributed)であるという条件(i.i.d. または iid)を暗黙のうちに仮定しています。
確率変数 $X$ から $n$ 個の値 $X_1$, $X_2$, ..., $X_n$ を引き出してくることは,統計学で,非常に大きな集団(母集団,population)からランダムに $n$ 個のもの(標本,sample)を選び出してくるのと同じことだと考えられます。
一つの標本の中に $n$ 個のものが入っているのです。$n$ 個の標本というと意味が違ってきます。$n$ は標本の「個数」ではなく標本の「大きさ」(size)といいます。英語でいえば $n$ samples ではなく a sample of size $n$ といいます。もっとも,日本ではこの違いをあいまいにすることが専門家にもしばしば見られます。
確率変数 $X$ の平均値(または期待値,expectation value または expectation)とは $\bar{X} = \frac{1}{n} (X_1 + X_2 + \cdots + X_n)$ の $n \to \infty$ での極限です。これを記号で $E(X)$ または $\langle X \rangle$ と書きます。$E(X)$ の値を1文字で表したいときは,よく $\mu$(ミュー)という文字を使います。$\mu$ は英語の m に相当するギリシア文字で,mean(平均)の頭文字です。
統計学のことばでは,$\mu = E(X)$ を母平均(population mean),$n$ が有限なときの $\bar{X} = \frac{1}{n} (X_1 + X_2 + \cdots + X_n)$ を標本平均(sample mean)といいます。$E(X)$ は一定の値ですが,$X$ から取り出した $X_1$ や $X_2$ などの個々の値,およびそれから計算した $\bar{X}$ は,標本ごとに違う値になります。つまり,$X_1$ などや $\bar{X}$ も確率変数といえます。それらの期待値はいずれも同じ値です:
\[ E(X_1) = E(X_2) = \cdots = E(\bar{X}) = E(X) = \mu \]期待値については次の式が成り立ちます($E(\cdots)$ の線形性):
\[ E(aX + bY) = aE(X) + bE(Y) \]ここで $a$,$b$ は定数です。これは $X$ と $Y$ が独立でなくても成り立つ便利な式です。さらに $X$ と $Y$ が独立ならば
\[ E(XY) = E(X)E(Y) \]も成り立ちます。
「独立」の定義を先に言わないといけませんでした。事象 $A$,$B$ が独立とは,$A$ と $B$ がともに起こる確率は $p(A \cap B) = p(A) p(B)$ のように個々の事象が起こる確率の積に等しいことです。確率変数なら $p(X=a \wedge Y=B) = p(X=a) p(Y=b)$ と書くほうがわかりやすいですね。期待値の定義は $E(X) = \sum x_i p(X=x_i)$ と書けますから証明も簡単でしょう。
確率変数 $X$ の期待値(母平均)を $\mu = E(X)$ とするとき,$X$ と母平均との差の2乗の期待値 $E((X - \mu)^2)$ を $X$ の分散(variance),統計学のことばでは母分散(population variance)といいます。記号ではよく $V(X)$ と表しますが,分散の値を文字で表すときはよく $\sigma^2$(シグマ2乗)と表します:
\[ \sigma^2 = V(X) = E((X - \mu)^2), \qquad \mu = E(X) \]この平方根
\[ \sigma = \sqrt{E((X - \mu)^2)} \]を標準偏差(standard deviation)といいます。$\sigma$(シグマ)は英語の s に相当するギリシア文字で,standard deviation の頭文字です。S.D. あるいは SD と書くこともあります。
確率変数 $X$,$Y$ が独立なら,和の分散は分散の和です。もっと一般に,$a$ と $b$ を定数として,$V(aX + bY) = a^2 V(X) + b^2 V(Y)$ が成り立ちます。特に,$V(X \pm Y) = V(X) + V(Y)$ です。標準偏差 $\sigma$ に焼き直せば,$\sigma^2_{X \pm Y} = \sigma^2_X + \sigma^2_Y$ という「三平方の定理」が成り立ちます。
$X$ から引き出した $n$ 個の値 $X_1$,$X_2$,...,$X_n$ については,
\[ E((X_1 - \mu)^2 + (X_2 - \mu)^2 + \cdots + (X_n - \mu)^2) = n\sigma^2 \]ですが,母集団の平均値 $\mu$ は実際には知ることのできない値ですので,この代わりに標本の平均値 $\bar{X} = \frac{1}{n}(X_1 + \cdots + X_n)$ を使うと,$\mu$ を使う場合より小さめの値になります(実際,$\bar{X}$ は $(X_1 - \bar{X})^2 + \cdots + (X_n - \bar{X})^2$ を最小にします)。後で証明するように,
\[ E((X_1 - \bar{X})^2 + (X_2 - \bar{X})^2 + \cdots + (X_n - \bar{X})^2) = (n-1) \sigma^2 \]です。そこで,
\[ s^2 = \frac{1}{n-1} ((X_1 - \bar{X})^2 + (X_2 - \bar{X})^2 + \cdots + (X_n - \bar{X})^2) \]と置くと,$s^2$ の期待値は母分散に一致します(これは $X$ の分布によらず成り立ちます。正規分布などは仮定していません):
\[ E(s^2) = \sigma^2 \]期待値が母分散に一致するということは,偏りがないということなので,$s^2$ は母分散 $\sigma^2$ の不偏推定量(an unbiased estimator of the population variance $\sigma^2$)であるといいます。あるいは,これを略して不偏分散(unbiased variance)ということもあります。
上の証明: $X = \mu + \varepsilon$ と置くと,
\[ \begin{align*} E(\varepsilon_i) &= 0 \\ E(\varepsilon_i^2) &= \sigma^2 \\ E(\varepsilon_i \varepsilon_j) &= 0 \quad (i \ne j) \end{align*} \]となります。この最後の式は $\varepsilon_i$ と $\varepsilon_j$ が独立であることから出ます($E(\varepsilon_i \varepsilon_j)$ は後で登場する共分散です)。すると,
\[ \begin{align*} \sum_{i=1}^n E((\varepsilon_i-\bar{\varepsilon})^2) &= \sum_{i=1}^n E\left( \left( \varepsilon_i - \frac{\varepsilon_1 + \varepsilon_2 + \cdots + \varepsilon_n}{n} \right)^2 \right) \\ &= \frac{1}{n^2} \sum_{i=1}^n E((\varepsilon_1 + \cdots + (n-1)\varepsilon_i + \cdots + \varepsilon_n)^2) \end{align*} \]ですが,この右辺の2乗を展開すると $E(\varepsilon_i \varepsilon_j) = 0$ のためにクロスタームが全部消え,$E(\varepsilon_i^2) = \sigma^2$ を代入すると結局 $(n-1)\sigma^2$ だけになります。
なぜ $\sum (X_i-\bar{X})^2$ が $n$ でなく $n-1$ に比例するのかは,次のような幾何学的な議論で直感的にわかるかもしれません。$(X_1, X_2, \ldots, X_n)$ は $n$ 次元空間の点です。しかし,$(X_1-\bar{X}, X_2-\bar{X}, \ldots, X_n-\bar{X})$ は,
\[ (X_1-\bar{X}) + (X_2-\bar{X}) + \cdots + (X_n-\bar{X}) = 0 \]という一つの制約条件を満たすので,次元の一つ少ない $n-1$ 次元空間の中に制約されます。つまり,自由度が一つ少ないので,ゆらぎの2乗和もその分だけ少なくなります。$n$ 次元が難しければ,3次元や2次元で考えてみてください。
別の言い方をすれば,同じデータから平均と分散を両方求めるなら,平均を求めた時点で自由度を一つ使ってしまっているので,分散は $n-1$ で割ります。平均が別に与えられているなら $n$ で割ります。
数学的な話が続いてしまいましたが,要するに,$X$ の平均 $\mu$ が最初からわかっている場合は,分散は
\[ \frac{1}{n}\sum_{i=1}^n (X_i-\mu)^2 \]で求め,同じデータから求めた平均 $\bar{X} = (X_1 + X_2 + \cdots)/n$ を使う場合は
\[ \frac{1}{n-1}\sum_{i=1}^n (X_i-\bar{X})^2 \]で求めるのが正しいのです。しかし,高校の数学の教科書では $n-1$ の説明が難しいのでこれらを区別せずにつねに $n$ で割っています。違いは小さいので,目くじらをたてるほどのことではありませんが,大学ではちゃんと区別しましょう。以下では高校教科書の流儀を「$n$ で割る分散」,正しい流儀を「$n-1$ で割る分散」と呼ぶことにします。
標本から求めた母分散の推定量を一般に標本分散(sample variance)といいます。しかし,本によって,定義がまちまちです。
$n$ で割るものについても,呼び名はまちまちです。
母分散の推定量の記号も $s^2$ を使うものや $\hat{\sigma}^2$ を使うものがありです。
Excelには $n$ で割る分散を求める varp() という関数があります(Excel 2010以降は var.p() も同義)。$n-1$ で割る分散はExcelでもRでも var() という関数で求めます(Excel 2010以降は var.s() も同義)。Excelの varp() に相当するものはRにはありません(だってそんなものを統計学者は使わないので)が,次のように打ち込めば作ることができます:
> varp = function(x) { var(x) * (length(x)-1) / length(x) }
これらを試してみましょう:
> x = 1:3 # x = c(1,2,3) でも同じ > var(x) [1] 1 > varp(x) [1] 0.6666667
母集団からランダムに取り出した標本でなくても,例えば10個の固定した値を4個と6個に分ける場合,両者を比較するには何で割った分散を使うかという問題についても,一貫して $n-1$ で割るほうが比較としては正しくなります:
> x = 1:10 > var(x) # n-1で割る分散 [1] 9.166667 > mean(combn(x, 4, var)) # xから4個選んだ組合せのvar()の平均 [1] 9.166667 > mean(combn(x, 6, var)) # xから6個選んだ組合せのvar()の平均 [1] 9.166667 > varp(x) # nで割る分散 [1] 8.25 > mean(combn(x, 4, varp)) # xから4個選んだ組合せのvarp()の平均 [1] 6.875 > mean(combn(x, 6, varp)) # xから6個選んだ組合せのvarp()の平均 [1] 7.638889
ここで combn(x, n, func) は,ベクトル x
から n 個選んだすべての組合せについて関数 func(x)
を適用した結果からなるベクトルを求める関数です。
正規分布の場合,真の分散 $\sigma^2$ との差の2乗和を最小にするには,$n+1$ で割る方式が一番良くなります。これは,分散の分布が右に長く延びた非対称な形なので,ある程度左右に縮めたほうが平均的には誤差の2乗和が減るためです。もっとも,実用的な意味はないでしょう。
標準偏差 $\sigma = \sqrt{\sigma^2}$ を標本から求める場合には,一般に次の式を使います。
\[ s = \sqrt{s^2} = \sqrt{\frac{1}{n-1} \sum_{i=1}^n (X_i-\bar{X})^2} \]$E(s^2) = \sigma^2$ でしたが,一般に $E(s) \neq \sigma$ です。$E(s)$ と $\sigma$ がどれくらい違うかは分布の形によります。
Rで標準偏差 $s$ を求めるには sd() を使います。
> x = 1:10 > sd(x) [1] 3.027650
$n$ で割る分散 varp() の計算式は,数学上は
と変形することができますが,こうすると非常に大きい数どうしの引き算となり,桁落ちと呼ばれる数値計算上の誤差が生じやすくなります。古いExcelはこの式を使って分散や標準偏差を計算していましたが,Excel 2003で修正されました。このことは単なる一つの例ですが,概してExcelは業界標準の計算法を使っていなかったり,そもそもどういう計算法を使っているかの情報公開が不十分であったため,数値計算や統計の専門家からは「Excelを使うな!」と言われてきました。varp() はこの声を反映して修正されたものと思われます。他にもたくさんExcelのおかしなところが指摘されているのですが,Excel 2007になってもこうした外部からの指摘をMicrosoftはほとんど製品の改良に反映していないように見えます。
Excelについての上の記述は,かなり古いものです。今は当時と比べて大きく改良されているはずです・・・と言いたいところですが,2022年時点でも,数値計算に関してはこのページの冒頭に書いたようなびっくりする仕様が残っています。ほかに,科学技術用途については,BOMなしUTF-8のCSVファイルをExcelで単純に開くと文字化けすることや,"Oct4" のような遺伝子名をCSVファイルから読み込むと化けることなど,たくさんの落とし穴がまだ残っています。
確率変数 $X$ の平均値 $\mu = E(X)$,分散 $\sigma^2 = E((X - \mu)^2)$ がわかっているとします。$X$ から引き出した数を $X_1$, $X_2$, ..., $X_n$ とすると,その平均値
\[ \bar{X} = \dfrac{X_1 + X_2 + \cdots + X_n}{n} \]の期待値は $\mu$ に一致します。一方,$\bar{X}$ の分散 $E((\bar{X} - \mu)^2)$ は,$\mu = 0$ の場合だけ考えればいいので,
\[ \begin{align*} E(\bar{X}^2) &= E\left( \left(\frac{X_1 + \cdots + X_n}{n} \right)^2 \right) \\ &= \frac{1}{n^2} (E(X_1^2) + \cdots + E(X_n^2)) \\ &= \frac{\sigma^2}{n} \end{align*} \]となり,$\bar{X}$ の分布は平均値が元と同じ $\mu$ で,分散が $\dfrac{\sigma^2}{n}$,したがって標準偏差は $\dfrac{\sigma}{\sqrt{n}}$ になります。
一般に,$\bar{X}$ のような統計量の標準偏差を標準誤差といいます。測定回数 $n$ を増やすと,平均値 $\bar{X}$ の標準誤差は $1/\sqrt{n}$ に比例して小さくなります。これが,できるだけ何度も測定して平均をとるべき理由です。測定回数が100倍になれば,標準誤差は 1/10 になります。
一番簡単な乱数は,ある範囲の数がまんべんなく出る一様乱数(uniform random numbers)です。Rの関数 runif(n) は,$0 < x < 1$ の範囲の一様乱数を $n$ 個取り出します(Rはデフォルトではメルセンヌ・ツイスターというアルゴリズム(日本の松本眞先生らによって考案されました)で乱数を発生します。RNGkind() で変更できます)。
> runif(1) [1] 0.388267 > runif(10) [1] 0.2146394 0.2765450 0.5433135 0.4784538 0.8147103 0.1141375 [7] 0.6488306 0.7947468 0.1698610 0.2440027
もっとたくさんの数,例えば百万個でやってみましょう。
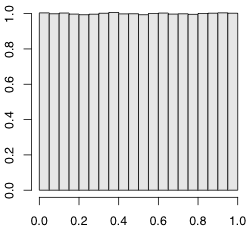
> x = runif(1000000) % 百万個の乱数 > hist(x, freq=FALSE) % ヒストグラム(度数分布図)を描く
ヒストグラム(度数分布図)を描く hist() を使いました。オプション freq = FALSE は縦軸の目盛りを,デフォルトの個数(frequency)でなく,密度(density)にすることを意味します。密度とは,棒グラフの棒の面積の和が 1 になるように付けた目盛りです。下で説明する確率密度関数の縦軸と同じものになります。

このヒストグラムを関数で表したものを確率密度関数(probability density function,略してp.d.f.)または単に密度関数といいます。数学的にいえば,任意の $a < b$ について,$a \leqq x \leqq b$ の範囲に乱数が入る確率が $\int_a^b f(x) dx$ になるように選ばれた関数 $f(x)$ が確率密度関数です。runif() の確率密度関数は
と表すことができます。
この runif() を二つ加えたらどうなるでしょうか。2倍するのではなく,独立な乱数を二つ加えるのです。
> x = runif(1000000) + runif(1000000) > hist(x, freq=FALSE)
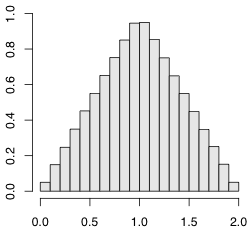
三個ならどうなるでしょうか。
> x = runif(1000000) + runif(1000000) + runif(1000000) > hist(x, freq=FALSE)
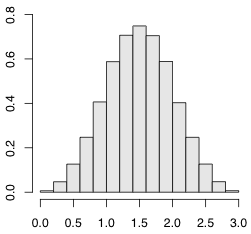
だんだん釣り鐘の形になってきました。
runif() は平均値が0.5ですので,0.5を引いて範囲を $-0.5 \leqq x \leqq 0.5$ にして考えましょう。この分散は
ですので,12個加えるとちょうど分散が1になります。
次の図が,runif() - 0.5 を12個加えた分布のヒストグラムです。
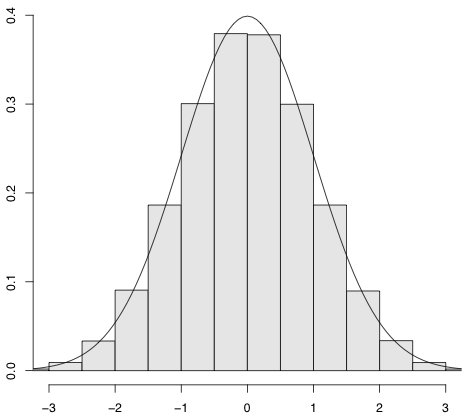
滑らかな曲線は
\[ f(x) = \frac{1}{\sqrt{2\pi}} \exp\biggl(-\frac{x^2}{2}\biggr) \]を描いたものです。ここで $\exp(z) = e^z$ は指数関数です。$e = 2.718\ldots$ は自然対数の底(てい)です。$\int_{-\infty}^{\infty} \exp(-x^2\!/2) dx = \sqrt{2\pi}$ ですので,これは確率密度関数です。この分布を標準正規分布(standard normal distribution)といいます。
$\int_{-\infty}^{\infty} \exp(-x^2\!/2) dx$ の計算ができなければ,Rで数値計算してみましょう。数値積分の関数 integrate() を使えば簡単にできます。積分範囲の指定には,無限大を表す Inf を使いました。
> integrate(function(x){exp(-x^2/2)}, -Inf, +Inf)
2.506628 with absolute error < 0.00023
> sqrt(2*pi)
[1] 2.506628
よって,$\int_{-\infty}^{\infty} \exp(-x^2\!/2) dx = \sqrt{2\pi}$ です。:-)
乱数を足し合わせる上の実験は,一様分布の乱数 runif() から出発しましたが,どんな分布から出発しても,まったく同じことが成り立ちます。
ただし分散が有限でなければなりません。後述のコーシー分布のような分散が無限大の分布では成り立ちません。
数学的に言えば,平均 $\mu$,分散 $\sigma^2$ の確率変数 $X$ がどんな分布であっても,そこから引き出した数 $X_1$, $X_2$, ..., $X_n$ の平均値
\[ \bar{X} = \dfrac{X_1 + X_2 + \cdots + X_n}{n} \]の分布は,平均値が元と同じ $\mu$ で,分散が $\sigma^2/n$ になりますので,
\[ \dfrac{\bar{X} - \mu}{\sqrt{\sigma^2 \! / n}} \]の分布は平均 0,分散 1 になります。ここまでは $n$ の値にかかわらず言えることです。ここで,$n$ が十分大きくなると,この分布は標準正規分布に近づきます。このことを中心極限定理といいます。
$X$ が標準正規分布ならば,$\sigma X + \mu$ は平均 $\mu$,分散 $\sigma^2$ の正規分布(normal distribution)になります。平均 $\mu$,分散 $\sigma^2$ の正規分布を $N(\mu, \sigma^2)$ と表します。標準正規分布は平均 0,分散 1 の正規分布ですので $N(0, 1)$ と表されます。
なお,正規分布を研究した数学者ガウス(Carl Friedrich Gauss,1777-1855)に敬意を表して,正規分布のことをガウス分布(Gaussian distribution)ともいいます。
変数がある範囲に入る確率を求めるには,密度関数を積分しなければなりません。そこで,あらかじめ密度関数 $f(x)$ を積分した
\[ F(q) = \int_{-\infty}^q f(x) dx \]を求めておくと便利です。この $F(q)$ を累積分布関数(cumulative distribution function,略してCDF)あるいは単に分布関数と呼びます。$F(q)$ がわかっていれば,確率変数 $X$ が $a \leqq X \leqq b$ の範囲に入る確率は $F(b) - F(a)$ で求められます。
分布関数 $p = F(q)$ の逆関数 $q = F^{-1}(p)$ を分位関数または分位点関数(quantile function)と呼びます。
Rには標準正規分布 $N(0,1)$ の
dnorm(x)pnorm(q) $= \int_{-\infty}^q \mathrm{dnorm}(x) dx$qnorm(p)rnorm(n)があります。下の図の色を付けた部分の面積が dnorm(x) です。
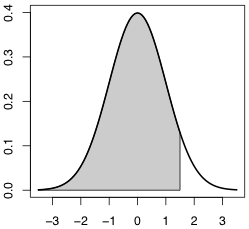
上の図の描き方:
x = (-35:15)/10 y = dnorm(x) plot(NULL, xlim=c(-3.5,3.5), ylim=c(0,0.4), xlab="", ylab="") polygon(c(x,x[length(x)],x[1]), c(y,0,0), col="gray") curve(dnorm, lwd=2, add=TRUE)
これらは,dnorm(x, mean=μ, sd=s) のように平均と標準偏差を与えることもできます。省略すれば dnorm(x, mean=0, sd=1) の意味になります。
正規分布の乱数を正規乱数といいます。
物理現象の測定では,測定誤差がほぼ正規分布することがよくあります。これに対して,他の多くの分野では,観測値そのものが正規分布することはまずありませんが,中心極限定理のおかげで,観測値の平均値はほぼ正規分布します。
正規分布 $N(\mu, \sigma^2)$ に従う変数 $X$ が平均±標準偏差の範囲内に入る確率,つまり $\mu - \sigma < X < \mu + \sigma$ になる確率は,標準正規分布 $N(0,1)$ に従う変数 $Z$ が $-1 < Z < 1$ になる確率に等しく,Rで次のようにして求められます。
> pnorm(1) - pnorm(-1) [1] 0.6826895
正規分布が左右対称であることを使えば,次のようにするほうが簡単です。
> 1 - 2 * pnorm(-1) [1] 0.6826895
つまり,ほぼ68%の確率で正規分布は $\mu \pm \sigma$ の範囲に入ります。
同様にして,$\mu \pm 2\sigma$,$\mu \pm 3\sigma$ に入る確率を求めてください。
逆に,$\mu \pm k\sigma$ の範囲に入る確率が与えられたときに $k$ の値を求めるには qnorm() を使います。例えば 95% の場合は
> qnorm(0.025) [1] -1.959964
ですので,ほぼ $\mu \pm 1.96\sigma$ です。ざっくり $\mu \pm 2\sigma$ で 95% と覚えておくと便利です。
現実のテストの分布は正規分布といえるでしょうか。2015年全国学力テスト中学理科の正答数の度数分布をrika_hist.csv(SJIS)・rika_hist-utf8.csv(UTF-8)として置いておきましたので,ヒストグラムを描き,平均と分散の同じ正規分布の密度関数を重ね書きしてみてください。
Scrapboxのほうに書いた正規分布の何がいいの?もご参照ください。
どれだけ正規分布から離れていても,分散が有限であれば,中心極限定理が成り立つので,その平均値は正規分布に近づきます。
しかし,世の中には中心極限定理の前提が満たされない本当に困る分布もあります。その有名な例が,密度関数が $1/(1 + ax^2)$ に比例するコーシー分布(Cauchy distribution)です。
分野によってはブライト・ウィグナー(Breit-Wigner)分布またはローレンツ(Lorentz)分布とも呼びます。自由度1の $t$ 分布の密度関数はコーシー分布に一致します。
この分散を計算しようとしても,$x^2/(1 + ax^2)$ の積分は発散してしまいます。そもそも $x/(1 + ax^2)$ も積分できません。
Rには密度関数が $1/(1+x^2)$ に比例するコーシー分布の
dcauchy(x)pcauchy(q) $= \int_{-\infty}^q \mathrm{dcauchy}(x) dx$qcauchy(p)rcauchy(n)があります。
実験をしてみましょう。100万個のコーシー分布の乱数を作ります。
x = rcauchy(1000000)
この度数分布を表示するために hist(x) としても,まともに表示されません。x = sort(x) で並べ替えて,最初の数個を head(x) で表示させたり,最後の数個を tail(x) で表示させたりすると,6〜7桁のとんでもない値が含まれることがわかります。そのため,平均 mean(x) を求めると,0からかなり外れてしまいます。このような分布は,分散はもとより,平均値を求めることにも意味がありません。強いて求めるなら,メジアンが最適です。
分散についても,平均を求める操作をメジアンに焼き直したMAD(median absolute deviation)と呼ばれるものを使えば,このような分布でも求めることができます。これは,データからメジアンを引いたものの絶対値のメジアン,つまりRで書くと
median(abs(x - median(x)))
になります。
ところで,標準正規分布の median(abs(x - median(x))) は qnorm(0.75) ≒ 1/1.4826 なので,正規分布の場合に標準偏差と比較しやすくするために,MADの定義を1.4826倍しておくことがあります。Rで mad(x) で求められる値はデフォルトでは
1.4826*median(abs(x - median(x)))
になっています。
MAD以外に,四分位範囲(interquartile range)もよく使われます。これは,順位が全体の1/4と3/4の値の差です。Rでは IQR() で求められます。補正しないMADのほぼ2倍に相当します。
正規分布に比べて外れ値(outliers)が非常に多い場合の分布のモデルにコーシー分布が使われることがあります。
以下の分布は頻繁に現れるので,Rの練習にもなりますので,乱数を発生させて度数分布を描き,理論的な密度関数と比べてみてください。
$\nu$ 個の数値 $X_1$, $X_2$, ..., $X_{\nu}$ が標準正規分布に従うとき,
\[ \chi^2 = X_1^2 + X_2^2 + \cdots + X_{\nu}^2 \]の分布を「自由度 $\nu$ のカイ2乗分布($\chi^2$ 分布)」(chi-square distribution with $\nu$ degrees of freedom)と呼びます(2乗は「にじょう」以外に「じじょう」と読むこともあります。これはもともと「自乗」(自分を乗算する)から来ています)。記号では $\chi^2(\nu)$ と書きます。$\chi$ はギリシア文字「カイ」(chi)です。自由度を表すのによく使う文字 $\nu$ はギリシア文字「ニュー」(nu)です。Rのマニュアルでは $\nu$ ではなく df と書かれています。
自由度 $\nu$ の $\chi^2$ 分布は,平均 $\nu$,分散 $2\nu$ で,その密度関数 $f(x)$ は $x^{\nu/2-1} e^{-x/2}$ に比例します。
$\chi^2$ は $X_1^2$, $X_2^2$, ... という独立な確率変数の和ですので,中心極限定理のため $\nu$ が大きいと正規分布に近づきます。
Rには自由度 $\nu$ の $\chi^2$ 分布の
dchisq(x, ν)pchisq(q, ν)
$= \int_0^q \mathrm{dchisq}(x, \nu) dx$qchisq(p, ν)rchisq(n, ν)が備わっています。
$X_1$, $X_2$, ..., $X_n$ が正規分布 $N(\mu, \sigma^2)$ に従うとき,標本分散
\[ s^2 = \frac{1}{n-1} \sum_{i=1}^n (X_i - \bar{X})^2 \]の分布は(定数倍を除いて)$\chi^2$ 分布です。正確には,$(n-1)s^2/\sigma^2$ が自由度 $n-1$ の $\chi^2$ 分布になります。
$X$ が標準正規分布 $N(0,1)$ に従い,$Y$ が自由度 $\nu$ の $\chi^2$ 分布に従うとき,
\[ t = \frac{X}{\sqrt{Y/\nu}} \]の分布を,自由度 $\nu$ のスチューデントの $t$ 分布(Student's $t$ distribution with $\nu$ degrees of freedom)あるいは単に自由度 $\nu$ の $t$ 分布と呼びます(Student はゴセット(W. S. Gosset,1876〜1937年)のペンネームです)。
自由度 $\nu$ の $t$ 分布の密度関数 $f(t)$ は $(1 + t^2/\nu)^{-(\nu+1)/2}$ に比例します。
特に,$X_1$, $X_2$, ..., $X_n$ が $N(\mu, \sigma^2)$ に従うとき,$\sigma^2$ の値にかかわらず,
\[ t = \frac{\bar{X} - \mu}{\sqrt{s^2 / n}} = \frac{\bar{X} - \mu}{s / \sqrt{n}} \]は自由度 $n-1$ の $t$ 分布に従います。
$n$ が大きいと $t$ 分布は正規分布に近づきます。母集団が正規分布でなくても,分散が有限であれば,多くの場合,$n$ が大きければ $t$ 分布が当たらずとも遠からずの結果を与えます。たとえば1〜5の5段階で答えるアンケートに50人が答え,分布が一様とするとき,$t$ に相当するものを100万回作ってみます。いろいろな方法がありますが replicate() を使うのが簡単でしょう。
tt = function() {
x = sample(1:5, 50, replace=TRUE)
(mean(x) - 3) / sqrt(var(x) / 50)
}
t = replicate(1000000, tt())
これが本物の $t$ 分布の95%区間から外れる割合を計算すると
> t0 = -qt(0.025, 50-1) > mean(abs(t) > t0) [1] 0.050288
となり,正しい値 0.05 と非常に近い値になります。$n$ や乱数の分布をいろいろ変えて,母集団が正規分布から外れたときの $t$ 分布からの外れの度合を感じ取ってください(上の 1:5 を c(1,2,2,3,3,3,4,4,4,4,5,5,5,5,5) のような適当な分布に変えてみてください)。ちなみに abs(t) > t0 は t と同じ長さのベクトルで,t の要素が t0 より大きければ TRUE,そうでなければ FALSE を要素に持ちます。それの平均 mean() を計算すると,TRUE = 1,FALSE = 0 として計算するので,結局 abs(t) > t0 が真である割合を数えていることになります。
アンケートなどのいわゆるリッカート尺度(Likert scale)と称される例えば5段階の選択肢は,$1 < 2 < 3 < 4 < 5$ という順序関係はあるものの,等間隔であることは保証されていません(つまり順序尺度ですが間隔尺度ではありません)。間隔尺度でないと,平均値を求める意味もないという批判もあります。しかし,間隔がまちまちでも,個数 $n$ が大きければ,中心極限定理で平均値の分布も $t$ 分布も正規分布に近づきます。有限の $n$ で実験してみるには,上の sample() の引数で 1:5 としているところの間隔を変えて例えば c(1,4,5,6,10) などとしてみます。(mean(x) - 3) の 3 も分布の平均値に変えます。sample() に確率分布を例えば prob = c(0.1, 0.2, 0.4, 0.2, 0.1) のような形で与えることもできます。
Rには自由度 $\nu$ の $t$ 分布の
dt(x, ν)pt(q, ν)
$= \int_{-\infty}^q \mathrm{dt}(x, \nu) dx$qt(p, ν)rt(n, ν)が備わっています。
$u_1$ と $u_2$ が独立な確率変数で,それぞれ自由度 $\nu_1$,$\nu_2$ の $\chi^2$ 分布に従うとき,
\[ F = \frac{u_1 / \nu_1}{u_2 / \nu_2} \]の分布を,自由度 $(\nu_1, \nu_2)$ の $F$ 分布($F$ distribution with $(\nu_1,\nu_2)$ degrees of freedom)といいます。
自由度 $(\nu_1,\nu_2)$ の $F$ 分布の密度関数 $f(F)$ は $F^{\nu_1/2-1} (1 + \nu_1 F / \nu_2)^{-(\nu_1+\nu_2)/2}$ に比例します。
特に,$X_1$, ..., $X_n$, $Y_1$, ..., $Y_m$ が $N(\mu, \sigma^2)$ に従うとき,$X_1$, ..., $X_n$ の標本分散を $s_1^2$,$Y_1$, ..., $Y_m$ の標本分散を $s_2^2$ とすれば,
\[ F = \frac{s_1^2}{s_2^2} \]は自由度 $(n-1,m-1)$ の $F$ 分布に従います。
Rには自由度 $(\nu_1, \nu_2)$ の $F$ 分布の
df(x, ν1, ν2)pf(q, ν1, ν2)
$= \int_0^q \mathrm{df}(x, \nu_1, \nu_2) dx$qf(p, ν1, ν2)rf(n, ν1, ν2)が備わっています。
高校「数学B」では,おもに正規分布に基づいて,仮説検定や区間推定の考え方を学びます。
例えば,歪んでいない硬貨を100回投げて表が $X$ 回出たとすると,$X$ は2項分布 $B(100, 0.5)$ に従う確率変数です。2項分布 $B(n, \theta)$ の平均は $n\theta$,分散は $n\theta(1-\theta)$ ですので,この2項分布の平均は $\mu = 100 \times 0.5 = 50$,分散は $\sigma^2 = 100 \times 0.5 \times (1 - 0.5) = 25$,標準偏差は $\sigma = \sqrt{25} = 5$ です。ここまでは厳密ですが,ここでこの2項分布を,これと同じ平均・分散の正規分布 $N(50, 25)$ で近似します。正規分布は平均を中心とする $\pm 1.96\sigma$ の範囲に 95% が入ります。この範囲外の事象が起きる確率は 5% 以下ですので,もしそのような事象が起きたら,「硬貨は歪んでいない」という最初の仮定(帰無仮説)は有意水準 5% で棄却されると考えます。つまり,100回投げて表が40回以下または60回以上出たら,硬貨は歪んでいると結論します。帰無仮説が棄却されない場合は,結論を保留します(歪んでいないと結論するのではありません)。
この「棄却する」という考え方は,誤解されやすいので,注意が必要です。例えば平均から $1.96\sigma$ 以上離れているデータは異常な「外れ値」なので削除するという考え方は間違いです。偏差値 30 以下や 70 以上の人を抹殺してはいけません。何度も繰り返せば,必ず $\mu \pm 1.96\sigma$ の範囲外の事象は起こります。
実際には,仮説検定を適用するのは,たいへん費用がかかるなどの理由で何度も繰り返すことができない場合に限られます。例えば新型コロナのワクチンが効くかどうかを調べるには大規模な治験が必要ですので,あらかじめ「まったく効かないという帰無仮説から(正規分布と仮定した場合)$1.96\sigma$ 以上離れた結果が出たら効果ありと判断する」といったルールを決めて治験を行います。
言い換えれば,データを中心として $\pm 1.96\sigma$ 以内の範囲に帰無仮説があれば,5% 水準で帰無仮説は棄却されません。この範囲を 95% 信頼区間といいます——という説明では雑すぎるので,以下でもうちょっとちゃんと説明します。
高校「数学B」でよく扱われるのは,データが正規分布 $N(\mu, \sigma^2)$ に従うと仮定して,平均 $\mu$ は未知,分散 $\sigma^2$ は既知で $\mu$ によらず一定とする場合です。この正規分布から大きさ $n$ の標本 $x_1, x_2, \ldots, x_n$ を取り出してその平均値 $\bar{x}$ を求めます。この $\bar{x}$ は正規分布 $N(\mu, \sigma^2/n)$ に従うはずですから,$\mu - 1.96\sigma/\sqrt{n} \leq \bar{x} \leq \mu + 1.96\sigma/\sqrt{n}$ を $\bar{x}$ が満たす確率は 0.95 です。この式を変形して $\bar{x} - 1.96\sigma/\sqrt{n} \leq \mu \leq \bar{x} + 1.96\sigma/\sqrt{n}$ を $\bar{x}$ が満たす確率は 0.95 と言っても同じことです。ここで現れる区間 $[\bar{x} - 1.96\sigma/\sqrt{n}, \bar{x} + 1.96\sigma/\sqrt{n}]$ を $\mu$ の 95% 信頼区間といいます。$\mu$ は 95% の確率でこの中に入りますが,確率変数は $\mu$ ではなく区間のほうです。
このように簡単に不等式が反転できるのは正規分布のような連続分布の特徴です。2項分布のような離散分布の信頼区間は,データによって棄却されない $B(n, \theta)$ の $\theta$ の範囲という定義に立ち戻る必要があります。$\theta$ が与えられたとき,$B(n, \theta)$ に従う確率変数 $X$ から求めた 95% 信頼区間 $[\theta_1(X), \theta_2(X)]$ が元の $\theta$ を含む確率は,一般に 95% になりません(95% 以上になります)。詳しくは検定と区間推定をご覧ください。
上の議論では,データが正規分布に従うと仮定しました。でも,現実のデータは正規分布に従うわけではありません。それなら上の議論は使えないかというと,そうではありません。データが正規分布から外れていても,そこからとった大きさ $n$ の標本の平均値 $\bar{x}$ は $n$ がある程度大きければほぼ正規分布に従います(中心極限定理)。上の議論は $\bar{x}$ が $N(\mu, \sigma^2/n)$ に従えば十分なので,データが正規分布という仮定を外しても近似としては十分正確です。
上の議論のもっと大きな問題点は,$\sigma^2$ すなわち母分散(母集団の分散)が既知と仮定しているところです。実際には母分散はわからないので,データから計算した分散の推定値で間に合わせることになります。すると,推定した母分散にも誤差が含まれますので,実際の 95% 信頼区間は上で計算したものより若干広くなることが考えられます。
このあたりの議論をもうちょっと詳しくすれば,このような場合に信頼区間を求めるには,正規分布ではなく,それより少し裾の広い $t$ 分布を使えばいいことがわかっています。このため,高校数学以外では,データが正規分布に従う場合でも,この $t$ 分布を使って検定します。正規分布を使って検定することはまずありません。
R には $t$ 分布を使った検定や区間推定をするための t.test() という関数が備わっています。例えば大きさ 5 のサンプル $\{1, 2, 3, 4, 5\}$ が得られたとき,母集団の平均値の 95% 信頼区間を求めるには,次のようにします。
> t.test(c(1, 2, 3, 4, 5))
One Sample t-test
data: c(1, 2, 3, 4, 5)
t = 4.2426, df = 4, p-value = 0.01324
alternative hypothesis: true mean is not equal to 0
95 percent confidence interval:
1.036757 4.963243
sample estimates:
mean of x
3
データの平均値は $\bar{x} = 3$ で,母集団の平均値 $\mu$ の 95% 信頼区間は [1.036757, 4.963243] です。なお,p-value = 0.01324 と出力されますが,これは母集団の平均値が 0 という帰無仮説を設定した場合の $p$ 値ですので,ここでは無視します。
なお,仮説検定で t.test() がよく使われるのは次のような場合です。集団 X から大きさ 5 の標本を取り出したら $\{1, 2, 3, 4, 5\}$ でした。集団 Y から大きさ 6 の標本を取り出したら $\{3, 4, 5, 6, 7, 8\}$ でした。分散については何の仮定もしません。両集団の平均値は等しいという帰無仮説を検定してください。
> x = c(1, 2, 3, 4, 5)
> y = c(3, 4, 5, 6, 7, 8)
> t.test(x, y)
Welch Two Sample t-test
data: x and y
t = -2.4019, df = 8.9894, p-value = 0.0398
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-4.8549526 -0.1450474
sample estimates:
mean of x mean of y
3.0 5.5
これは $t$ 検定に基づいてウェルチ(Welch)という人が考えた方法を使っています。「両群の母分散が等しいと仮定しない場合の $t$ 検定」ということもあります。$p$ 値は 0.0398 ですので,水準 0.05 で両集団の母平均は有意に異なります。また,両集団の母平均の差の 95% 信頼区間は [-4.8549526, -0.1450474] です。
なお,X,Y 両群の母分散が何らかの理由で等しいと仮定できる場合は,次のようにします。
> t.test(x, y, var.equal=TRUE)
Two Sample t-test
data: x and y
t = -2.3619, df = 9, p-value = 0.04247
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-4.8944379 -0.1055621
sample estimates:
mean of x mean of y
3.0 5.5
結果がほんの少し変わりました。通常は母分散が等しいと仮定できる理由はないので,先ほどの Welch の検定のほうを使います。
母分散が等しいかどうかの検定をしてからどちらの $t$ 検定を使うかを決めると書いている教科書もありますが,そのような方法はお勧めできません。
より詳しくは t検定 のページをご覧ください。
Last modified: