歪んだ硬貨があって,投げると確率 $\theta$ で表が出て,確率 $1 - \theta$ で裏が出るとします。この硬貨を $n$ 回投げて,表が $r$ 回出る確率を求めてください。
これが2項分布(binomial distribution)の問題です。答えは
\[ _nC_r \theta^r (1-\theta)^{n-r} \]です。$_nC_r$ は $n$ 個から $r$ 個を選ぶ組合せ(combination)の数で,英語ではよく $n$ choose $r$ と読みます。階乗(!)を使えば
\[ _nC_r = \frac{n!}{r!(n-r)!} \]と表せます。
Rでは,例えば $_{10}C_3$ は choose(10,3)
と打てば求められます。
> choose(10, 3)
[1] 120
投げると確率 0.4 で表が出る硬貨を10回投げて表が3回出る確率 $_{10}C_3 \cdot 0.4^3 \cdot 0.6^7$ は
> choose(10, 3) * 0.4^3 * 0.6^7
[1] 0.2149908
です。
同じ値は dbinom(3, 10, 0.4) という関数でも求められます。
> dbinom(3, 10, 0.4)
[1] 0.2149908
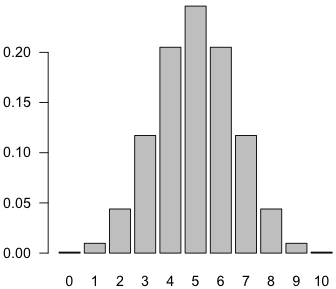
投げると確率 0.5 で表が出る硬貨を10回投げて表が0〜10回出る確率を全部出力するには次のようにします。
> dbinom(0:10, 10, 0.5)
[1] 0.0009765625 0.0097656250 0.0439453125 0.1171875000
[5] 0.2050781250 0.2460937500 0.2050781250 0.1171875000
[9] 0.0439453125 0.0097656250 0.0009765625
これをグラフにするには次のように打ち込みます。
barplot(dbinom(0:10, 10, 0.5), names.arg=0:10)

デフォルトでは $y$ 軸の文字が横向きになります。上の図のようにするには,barplot() にオプション las=1 を与えるか,またはあらかじめ
par(las=1)
と打ち込んでおきます。par() は図を描く際のオプション(parameter)を指定するコマンドです。las は label style の意味です。詳しい説明はRに
?par
と打ち込んで出るヘルプを見てください。
確率なので,全部加えると 1 になります。
> sum(dbinom(0:10, 10, 0.5))
[1] 1
ちなみに,dbinom() の累積を求める pbinom() という関数もあります。
> pbinom(0:10, 10, 0.5)
[1] 0.0009765625 0.0107421875 0.0546875000 0.1718750000
[5] 0.3769531250 0.6230468750 0.8281250000 0.9453125000
[9] 0.9892578125 0.9990234375 1.0000000000
[追記] この説明に使うJavaScriptのプログラムを作りました。
硬貨を10回投げて表が2回しか出ませんでした。この硬貨は歪んでいるでしょうか。
ある母集団から10人をランダムに選んで聞いたところ,賛成2人,反対8人でした。母集団全体でも反対のほうが多いと言えるでしょうか。
これらの問いについて考えるために,仮に硬貨は歪んでいない(あるいは母集団全体では賛否が等しい)というモデル(帰無仮説,null hypothesis)を設定します。そして,この帰無仮説が正しかった場合に,実際に観測された事象か,それより珍しい事象の確率の合計を求めます。この場合は,表が0〜2回・8〜10回出る確率の合計です。この確率の合計を $p$ 値(ピーち,$p$-value)といいます。
$p$ 値が非常に小さければ,実際に起きた事象はこのモデルでは説明しにくいので,たぶん硬貨は歪んでいる(あるいは賛否は等しくない)と推測します。$p$ 値が大きければ,これだけのデータでは何も言えません。
$p$ 値が大きいか小さいかの境界(有意水準)を仮に 0.05 として,$p \leqq 0.05$(または $p < 0.05$)であれば帰無仮説からの外れが「統計的に有意」(statistically significant)である,あるいは「帰無仮説は棄却(reject)される」ということがあります。0.05 という値に特に意味はありませんが,伝統的によく使われています(物理学では通常もっともっと厳しい条件を課します)。
さて,硬貨投げで表も裏も 1/2 の確率で出るという帰無仮説では,表が $r$ 回出る確率は $_{10}C_r (1/2)^{10}$ です。表が0,1,2,8,9,10回出る確率はそれぞれ
> dbinom(c(0, 1, 2, 8, 9, 10), 10, 0.5)
[1] 0.0009765625 0.0097656250 0.0439453125 0.0439453125
[5] 0.0097656250 0.0009765625
で,この合計,すなわち $p$ 値は
> sum(dbinom(c(0, 1, 2, 8, 9, 10), 10, 0.5))
[1] 0.109375
になります。同じことが
> pbinom(2, 10, 0.5) * 2
[1] 0.109375
でも求められます。また,後で詳しく述べますが,binom.test()
という関数を使えば,このような計算(2項検定)が簡単にできます。
> binom.test(2, 10, 0.5)
Exact binomial test
data: 2 and 10
number of successes = 2, number of trials = 10, p-value = 0.1094
...
つまり,表が2回出るという事象の $p$ 値は 0.1094 ほどです。したがって,有意水準を 0.05 とすれば,表裏の差は統計的に有意ではありませんし,アンケートであればこんなに少人数の結果から「賛成が少ない」という結論を導いてはいけないということになります。
表が1回(賛成が1人)なら,$p$ 値は 0.02 ほどになり,水準 0.05 で有意になります。
これが,フィッシャー(R. A. Fisher,1890〜1962年)が「有意性の検定」(tests of significance, significance tests)と呼んだ方法の考え方です。
ここでは,実際に生じた事象またはそれより珍しい事象の生じる確率の合計として $p$ 値を定義しました。これは2項分布のような山の形の分布では両側の部分の確率になりますので,両側検定といいます。一方,実際に生じた事象の側(左または右)だけを考える方法もあります。これは片側検定といいます。例えば表が2回出た場合の片側 $p$ 値は,表が0回・1回・2回出る確率の合計です。
ICH(医薬品規制調和国際会議)の定めるICH E9「臨床試験のための統計的原則」というガイドラインでは,「原則として片側仮説を検証する場合は2.5%、両側仮説の場合は5%とすること」とされています。また,「有意性検定の結果を報告する際には、限界値を越えたかどうかではなく、正確なp値(例えば「p=0.034」)を報告すべきである」と書かれています。
帰無仮説は現象の理解を助けるために設定した一つのモデルです。そのモデルと現実のデータとの整合性の度合を確率のことばで表したのが $p$ 値です。$p$ 値が非常に小さければ,モデルとデータは両立しにくいので,より良いモデルを考えなければならないことになります。
$p$ 値は「帰無仮説が正しい確率」ではありません。どんな硬貨でも少しは歪んでいます。母集団の賛否の割合がぴったり等しいことなどありえません。したがって,「帰無仮説が正しい確率」というものがもし定義されるなら,それは 0 であるというのが妥当でしょう。
$p$ 値は,標本の大きさ(調べた個数)によって大きく変化します。例えば歪んだ硬貨を調べる場合,投げた回数が非常に多ければ,検定の「感度」がうんと高くなるので,実用上無視できるほどのちょっとした歪みでも $p$ 値は非常に小さくなります。逆に,本当に表が出やすい硬貨でも,投げた回数が少なければ $p$ 値はなかなか小さくなりません。$p$ 値が小さくないからといって,帰無仮説が正しいというわけではありません。
$p$ 値が(有意水準より)小さくならなかったとき「帰無仮説を採択(accept)する」ということがありますが,これは誤解しやすい言葉です。「帰無仮説を棄却できない」あるいは「わからない」というほうが正しいでしょう。差がなかったのではなく,測定の感度が悪くて差が見つけられなかっただけです。
フィッシャーの「有意性の検定」は,後にネイマン(Jerzy Neyman, 1894〜1981)とピアソン(Egon Pearson, 1895〜1980)の「統計的仮説検定」(statistical hypothesis testing)の数学理論へと発展します。ただ,ネイマンたちの問題の設定のしかたを科学の研究にそのまま適用しようとすると,実験前に有意水準を例えば 0.05 と決めたなら,必ず $p = 0.049$ で帰無仮説を棄却して $p = 0.051$ で棄却しないという杓子定規な判断をすることになり,この点にフィッシャーは非常に違和感を感じました。
科学の歴史の中には,$p$ 値が非常に小さかったことが後でひっくり返ることがいくらでもあります。$p$ 値を求めるのはいいのですが,$p$ 値だけで機械的に判断するのが科学的というわけではありません。一方で,工場の品質管理のように,自動判断が必要な場合には,$p$ 値は有用です。
ニュートリノという素粒子の基礎研究で小柴昌俊氏が2002年にノーベル物理学賞を受賞しました。そして,2015年のノーベル物理学賞は,ニュートリノに質量があることを実験的に示した梶田隆章氏たちに与えられました。スーパーカミオカンデで行われた梶田氏たちの実験は,ニュートリノの質量を直接測るものではありませんが,ニュートリノに質量がなければ絶対に観測されない「ニュートリノ振動」という現象を観測しました。この場合,ニュートリノに質量がないと仮定して,そのような観測結果(またはもっと極端な結果)が得られる確率が $p$ 値です。「ニュートリノに質量がある確率」は求められません。ちなみに物理学では正規分布の $5\sigma$ に相当する有意水準で「発見」を判断します。通常の水準 0.05 は正規分布のほぼ $2\sigma$ の両側確率に相当します。$5\sigma$ に相当する片側確率は pnorm(-5) で求められます(ほぼ $3 \times 10^{-7}$ です)。
物理学(特に素粒子論)の $5\sigma$ の起源については Origin of "5𝜎" threshold for accepting evidence in particle physics? をご覧ください。
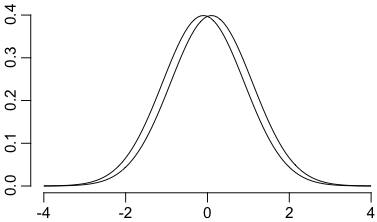
右の図は,分散がいずれも 1 で平均値が 0.2 だけ離れている二つの正規分布 $N(-0.1,1)$,$N(0.1,1)$ です。これらの群の平均値の違いを検出したければ,各群およそ200個ずつ調べる必要があります。それだけ集めて調べれば統計的に有意な差が得られる公算が高いのですが,逆に,それだけ集めないと違いがわからないほどであれば実質的な差はほとんどないとも言えます。実際,各群からランダムに1個ずつ取り出したとき,左の群のものが右の群のものより大きくなる確率は44%以上もあります。
「実質的な差」がなくても,科学的に意味がないわけではありません。ノイズに埋もれて,非常に大きなサンプルを調べなければ統計的に有意な結果が得られないような現象が,科学的には非常に重要であることは,よくあることです。「どんなに $p$ 値が小さくても,例えば相関係数が 0.1 といった値であれば,実質的な意味はない」はあくまで一般論で,ケースバイケースで考えるべきことです。
例えば,ニュートリノの質量が 0 でないという発見は,その質量がどんなに小さくても,ノーベル賞級の意味があります。また,血液型と性格に関連があることが示されれば,その関連がどんなに小さくても,性格の生理学的起源に関する重要な発見であると思われます(未だに一貫した結果は得られていません)。
なお,平均値の小さな違いでも,極端な値の割合に大きな違いが出ることがあります。さきほどの二つの正規分布で $x \geqq 3$ の確率を求めると,
> pnorm(-3.1)
[1] 0.0009676032
> pnorm(-2.9)
[1] 0.001865813
のように,千個に1個の割合が,千個に2個の割合に増えます。この違いが実質的な意味を持つことは十分考えられます(これらの数値は分布が正確な正規分布であることに強く依存するので,単なる例としての意味しかありません)。
右上の図は次のようにして描きました:
curve(dnorm(x-0.1), xlim=c(-4,4), frame.plot=FALSE, xlab="", ylab="")
curve(dnorm(x+0.1), add=TRUE)
各群からランダムに1個ずつ取り出したとき,左の群のものが右の群のものより大きくなる確率が44%以上もあることは,次のような数値積分で調べられます:
integrate(function(x){dnorm(x+0.1)*pnorm(x-0.1)}, -Inf, +Inf)
あるいはシミュレーションで次のようにして調べられます:
mean(rnorm(1000000,mean=0.1) < rnorm(1000000,mean=-0.1))
7個の変数についてデータを収集しました。それらの二つずつについて相関係数を調べ,$_7C_2 = 21$ 個の相関係数を得ました。うち一つが統計的に有意でした。有意な結果が得られたと言えるでしょうか?
21回の検定をして,偶然に5%水準で有意になる回数は,期待値として1回以上あります。つまり,まったく何の関係もなくても,21回のうち1回は有意な結果が出てしまいます。こういうのを多重比較(multiple comparisons)といって,注意が必要です。
ポーカーをやったらツーペアが出ました。ツーペアが出る確率は約 1/21 なので,たった1回でツーペアが出るのは,5%水準で有意な珍しい事象だと言ってもかまいません。でも,何度も試していいなら,ツーペアは必ず出ますよね。
血液型と性格の関係を調べるために,A/B/AB/O,男/女,いろいろな性格検査の項目をごちゃごちゃやっているうちに,いくつか統計的に有意な結果が見つかりました。そりゃあ,何度もやっているうちにいつかは有意な結果は出ますよね。
いろいろやってみて有意な結果が出るまで $p$ 値の計算を繰り返すことを,最近の言葉では $p$ ハッキングといいます。
5%水準で有意な結果を載せる論文誌の内容は,ただでさえ20個に1個はウソです。さらに,研究者は有意な結果が得られなかった研究は葬り去り,有意な結果が得られた研究だけ論文にして投稿するでしょうから,たとえ全部がウソでも,20回の研究のうち1回は有意な結果が出て,あわよくば論文として出版されます。だとすれば,ウソ研究の割合は1/20よりずっと多いはずです。これを出版バイアスといいます。実際,論文誌に載った研究結果が再現できるか試したところ,再現できない割合は1/20よりずっと大きいことがわかりました。
$p$ ハッキングや出版バイアスを防ぐため,最近では研究の事前登録(pre-registration,プレレジ)という仕組みが行われるようになりました。あらかじめどんな研究をして,何について有意かどうか調べるかということを,だれにも見られるところに登録しておく仕組みです。ただ,プレレジが制度として確立している研究分野はごくわずかです。
[追記] 以下の説明は詳しすぎるので,授業ではJavaScriptのプログラムを使って説明します。
なお,高校「数学B」では,2項分布 $B(n, \theta)$ の平均が $n\theta$,分散が $n\theta(1-\theta)$ であることから,同じ平均と分散を持つ正規分布で近似して扱うことが多いと思います(中心極限定理から $n \to \infty$ で正規分布になります)。
検定の概念が理解できれば,次に,モデルのパラメータ $\theta$ をいろいろ変えてみて,データがどの範囲のモデルと両立し得るかを調べてみましょう。
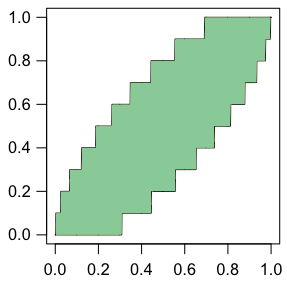
2項分布
\[ _nC_r \theta^r (1-\theta)^{n-r} \]で,以下では $n = 10$ の場合を考えます。このとき,例えば $\theta = 0.5$ という帰無仮説とデータが水準 0.05 で両立し得る(帰無仮説が棄却されない)のは,$r$ が 2 以上 8 以下のとき,つまり,割合 $r/n$ が 0.2 以上 0.8 以下のときです。$\theta$ をいろいろ変えると,この範囲は右図のように階段状に変わります。色を付けた部分が,横軸 $\theta$ に対応する帰無仮説が水準 0.05 で棄却されない縦軸 $r/n$ の範囲です。
右図は次のようにして描きました(色はPhotoshopで付けました):
par(las=1)
curve(qbinom(0.025,10,x)/10, xlim=c(0,1), n=1001, asp=1)
curve(qbinom(0.975,10,x)/10, n=1001, add=TRUE)
ここで,逆にデータ $r/n$(縦軸)が与えられたときに図を横に見ていけば,そのデータと両立する $\theta$ の範囲がわかります。この範囲のことを,$\theta$ の「95%信頼区間」(confidence interval,CI)と呼びます。つまり,
と定めます。
「つまり $\theta$ の真の値は95%の確率でこの区間に入る」―― と言いたいところですが,そもそもモデル自体が正しいかどうかわかりませんし(というかモデルは常に近似に過ぎませんし),$\theta$ の「真の値」が存在したとしても,それは定数であって,確率変数ではありませんので,「$\theta$ が何々の確率でこの区間に入る」という意味がはっきりしないと思います。次のように考えるとわかりやすいでしょう。
まず,何でもいいから $\theta$ の値を一つ固定します。例えば $\theta = 0.5$ としましょう。すると,2項分布モデルから計算して,95%以上(正確には後で述べるように約97.85%)の確率で $r/n$ は 0.2 以上 0.8 以下になりますが,上の図をよく見て考えれば,$r/n = 0.2$ から 0.8 までに対応する信頼区間のどれにも $\theta = 0.5$ が含まれます(当然!)ので,確かに95%以上の確率で,$r/n$(これが確率変数です)に対応する区間(これも確率変数になります)に,$\theta = 0.5$(これは定数です)が含まれることになります。このことは $\theta$ をどんな値に固定しても言えることです。
さらに言い換えれば,モデル(ここでは2項分布)さえ正しければ,何度も何度も実験を繰り返して,毎回得られた $r/n$ に対応する95%信頼区間を列挙し続ければ,そのうち95%(以上)が正しいということができます。こちらのほうを信頼区間の定義とすることもできます(その場合には「以上」を除くこともできますが,離散分布の場合に「以上」を除くのは簡単ではありません)。
上に示した97.85%という値は次のようなさまざまな方法で求められます。
> pbinom(8,10,0.5) - pbinom(1,10,0.5)
[1] 0.9785156
> 1 - 2 * pbinom(1, 10, 0.5)
[1] 0.9785156
> sum(dbinom(2:8, 10, 0.5))
[1] 0.9785156
以上が(2項分布のような離散的な場合も含めた)古典的な信頼区間の考え方です。より詳しくは次の文献をご覧下さい。
有意性の検定に基づく信頼区間の定義はシンプルですが,2項分布のような離散分布の場合,同じことをずっと続けた場合に $\theta$ が区間内に入る確率は95%以上になり,ぴったり95%になりません。原理的にどんな場合にもぴったり95%にすることは離散分布である限り無理なのですが,できるだけ95%に近づけようという研究がいろいろあります。詳しくは,例えば次の論文とそれに続くコメント集,特に Casella のコメント,そこで言及されている論文をご覧ください。
データから信頼区間を決めるやりかたそのものにランダムさを導入すれば,信頼区間に入る確率をぴったり95%にすることが可能ですが,データから一意的に定まらない信頼区間は奇異ですし,そこまでする必要はないでしょう。
Rには上の考え方に従って2項分布の検定と信頼区間を求める関数 binom.test()
があります。例えば実際に得られた割合が10個のうち2個だったとすると,
> binom.test(2, 10, 0.5)
Exact binomial test
data: 2 and 10
number of successes = 2, number of trials = 10, p-value = 0.1094
alternative hypothesis: true probability of success is not equal to 0.5
95 percent confidence interval:
0.02521073 0.55609546
sample estimates:
probability of success
0.2
ということで,$\theta = 0.5$ という帰無仮説についての $p$ 値は 0.1094 で,$\theta$ の95%信頼区間は $0.025 \leqq \theta \leqq 0.556$ であることがわかります(このことを「$\theta$ の95%信頼区間は $[0.025, 0.556]$ である」というふうに書きます)。
もっと大きな場合にやってみましょう。
新聞社などの行う世論調査は,今では機械でランダムに電話をかけるRDDという方式がよく使われます。回答数は1000〜2000人程度です。
例えば1000人のうち200人が現内閣を支持すると答えたとすると,
> binom.test(200, 1000) # 第3引数を省略するとθ=0.5についてのp値を求める
Exact binomial test
data: 200 and 1000
number of successes = 200, number of trials = 1000, p-value < 2.2e-16
alternative hypothesis: true probability of success is not equal to 0.5
95 percent confidence interval:
0.1756206 0.2261594
sample estimates:
probability of success
0.2
というわけで,$\theta = 0.5$ という帰無仮説についての $p$ 値が $2.2 \times 10^{-16}$ より小さいということはあまり役に立ちませんが,95%信頼区間が $[0.176, 0.226]$ であることがわかります。つまり,「20%」と言っても,実際は18%かも22%かもしれないので,小数点以下まで表示する意味はありません。
標本サイズ $n$ が大きくなると,ギザギザな図は滑らかになり,2項分布は正規分布で近似できるようになるので,2項分布の分散が $n\theta(1 - \theta)$ であることを使えば,観測された割合を $r/n$ とすると,$\theta$ の95%信頼区間はほぼ $r/n \pm 1.96 \times \sqrt{(r/n)(1 - r/n) / n}$ となります。1000人のうち200人がYesと答えた場合には,この近似では $\theta = 0.20 \pm 0.025$ となり,さきほどの厳密な結果とほぼ一致します。
めでたしめでたし,という話にしたかったのですが,2項分布のような離散分布で,分布が左右非対称の場合は,重箱の隅に,まだまだいろいろな魑魅魍魎がいます。その一例を紹介します。
Rの binom.test() で $\theta = 0.5$ 以外の場合,$p$ 値が 0.05 より小さくなっても,帰無仮説の $\theta$ が95%信頼区間に含まれるということがよくあります。例えば
binom.test(2, 15, 0.4)
をしてみると,$p = 0.036$ ですから $\theta = 0.4$ は5%水準で棄却されるはずなのに,95%信頼区間は $[0.0166, 0.4046]$ で,これは $\theta = 0.4$ を含みます。どちらが正しいのでしょうか。
この理由は以下の通りです。まず,Rの binom.test() は信頼区間を上で説明した一般的な方法(Clopper and Pearson の方法)で求めています。この方法は,95%信頼区間なら,片側2.5%点が観測値になるような2点で信頼区間を定義します。一方で,binom.test() の出力する $p$ 値は,Sterne の方法で求めています。これは,Fisherの正確検定と同様に,帰無仮説のもとで観測値が生じる確率およびそれより小さい確率を合計する方式です。これらは,それぞれ信頼区間,$p$ 値を求める標準的な方法ですが,微妙に異なる方法であるため,上の例のように矛盾した結果を与えることがあります。
さらに別の方式として,Blaker の方法は,もう一方の側の確率として,片側 $p$ 値を超えない範囲で実際に得られる最大の値を使います。
この Clopper and Pearson,Sterne,Blaker の方法を選べるようにし,$p$ 値と信頼区間を同じ方法で求めるようにしたのが,exactciパッケージの binom.exact() 関数です。オプションで次の三つが選べます:
tsmethod="minlike":binom.test() で $p$ 値を求める際に使われるSterneの方法を使うtsmethod="central":binom.test() で信頼区間を求める際に使われるClopper and Pearsonの方法を使うtsmethod="blaker":Blakerの方法を使う一般に Sterne や Blaker の方法のほうが $p$ 値が小さくなり,したがって信頼区間が狭くなるのですが,たとえば標本の大きさを増やして $p$ 値が減るはずなのに,実際には $p$ 値が増えてしまうといった好ましくない現象も生じることがあります(下の Vos and Hudson 参照)。
どうするのがいいかは言い難いのですが,$p$ 値よりは信頼区間のほうが大切ですし,信頼区間を求めるClopper and Pearsonの方法はもう標準になっているので,それで信頼区間を求め,$p$ 値のほうは特に報告しない(信頼区間に帰無仮説の母数が入っているかどうかで判断してもらう)というのはどうでしょうか。これなら標準の binom.test() で問題ありません。
Last modified: