確率変数 $X$ の分布が正規分布 $N(\mu, \sigma^2)$ であり，そこから $n$ 個取り出した標本の平均値を
\[ \bar{X} = \frac{X_1 + X_2 + \cdots + X_n}{n} \]とし，標本分散を
\[ s^2 = \frac{1}{n-1} \sum_{i=1}^n (X_i - \bar{X})^2 \]とすると，
\[ t = \frac{\bar{X} - \mu}{\sqrt{s^2 / n}} \]は，$\sigma^2$ の値にかかわらず，自由度 $n - 1$ の $t$ 分布になります。このことを使って，母集団が平均 $\mu$ の正規分布かどうかを検定できます。
実際には $X$ が正規分布でなくても，$n$ が大きければ中心極限定理により $\bar{X}$ は正規分布に近づくので，この検定は母集団が正規分布かどうかには鈍感です。データの分布が正規分布かどうかの検定をしてから $t$ 検定を行う必要はまったくありません。
10人の患者にある睡眠薬を飲ませたところ，睡眠時間がそれぞれ次の時間だけ増えました（Arthur R. Cushny and A. Roy Peebles, The Journal of Physiology 32, 501-510 (1905)）：
| 1.9 | 0.8 | 1.1 | 0.1 | -0.1 | 4.4 | 5.5 | 1.6 | 4.6 | 3.4 |
Rに x = scan() と打ち込んで，1: のようなプロンプトが出たら，上の表の数値10個をそこにコピペし，最後にEnterを1〜2回打ち込んでください。あるいは
x = c(1.9, 0.8, 1.1, 0.1, -0.1, 4.4, 5.5, 1.6, 4.6, 3.4)
というコマンドをRにコピペしても同じです。
検定の前に，まずはグラフを描いてみましょう。一例です：
boxplot(x)stripchart(x, pch=16, at=0, method="stack")hist(x, right=FALSE, col="gray")データのイメージがつかめたら，$t$ 検定してみましょう。
t.test(x)
結果は次のように表示されます：
One Sample t-test
data: x
t = 3.6799, df = 9, p-value = 0.005076
alternative hypothesis: true mean is not equal to 0
95 percent confidence interval:
0.8976775 3.7623225
sample estimates:
mean of x
2.33
下から読んでいくと，このデータの平均値は 2.33 で，その95%信頼区間は $[0.90, 3.76]$ だということがわかります（54分〜3時間46分）。信頼区間は 0 を含んでいませんので，これだけで「平均値が 0」という帰無仮説は棄却されることがわかりますが，念のため $p$ 値を見てみると，0.005 という小さい値です。どうやら，データは帰無仮説を支持していないようです。つまり，睡眠薬の効果はあったといえます。
「母集団の平均値が 0」という帰無仮説を検定したいかどうかにかかわらず，t.test() は平均値の信頼区間を求めるのに便利です。グラフに描くなら，信頼区間をエラーバーとして書き込みましょう。
正規分布を仮定しないノンパラメトリックな検定法として符号検定とWilcoxonの符号付き順位検定があります。ただし，このような研究では「睡眠時間が増えたかどうか」ではなく「何時間増えたか（95%信頼区間の意味で）」が意味を持ちますので，臆せず $t$ 検定を使いましょう。
確率変数 $X$ から引き出した $m$ 個の値 $X_1$, $X_2$, ..., $X_m$ と，確率変数 $Y$ から引き出した $n$ 個の値 $Y_1$, $Y_2$, ..., $Y_n$ があったとします。どちらの分布も正規分布と仮定したとき，それらの母平均が等しいという仮説を検定してみましょう。
それぞれの標本平均を $\bar{X}$, $\bar{Y}$, 標本分散を $s_X^2$, $s_Y^2$ とします。
二つの標本をプールしたものから次の式で分散の推定値 $s^2$ を求めます：
\[ \begin{align*} s^2 &= \frac{(X_1 - \bar{X})^2 + \cdots + (X_m - \bar{X})^2 + (Y_1 - \bar{Y})^2 + \cdots + (Y_n - \bar{Y})^2}{m + n - 2} \\ &= \frac{(m - 1) s_X^2 + (n - 1) s_Y^2}{m + n - 2} \end{align*} \]このとき，
\[ t = \frac{\bar{X} - \bar{Y}}{\sqrt{s^2 \big( \frac{1}{m} + \frac{1}{n} \big) }} \]は自由度 $m + n - 2$ の $t$ 分布に従います。
一般には，$X$ の母分散も $Y$ の母分散も不明であるなら，それらが等しいかどうかも不明のはずです。この場合によく用いられる方法は，
\[ t = \frac{\bar{X} - \bar{Y}}{\sqrt{s_X^2 \big/ m + s_Y^2 \big/ n}} \]が近似的に自由度
\[ \nu = \frac{(s_X^2 \big/ m + s_Y^2 \big/ n)^2}{\dfrac{(s_X^2 \big/ m)^2}{m-1} + \dfrac{(s_Y^2 \big/ n)^2}{n-1}} \]の $t$ 分布に従うことを使うものです。これはWelch（ウェルチ）が次の論文で提案した方法の一つで，広く用いられています。
この自由度 $\nu$ は整数になりませんが，$t$ 分布は $\nu$ が整数でない場合にも拡張できます。
分散が等しいかどうかわからない場合は，下の「分散が等しいかどうか不明の場合」をご覧ください。
Welchの検定は，片方の標準偏差を 0 にすれば，1標本の $t$ 検定に帰着します。
2組の患者たちに痛みのレベルを報告してもらったところ，次のような結果を得ました (T. Lumley, Biometrics 52, 354-361 (1996))。
| x | 1 | 2 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 2 | 4 | 1 | 1 |
|---|
| y | 3 | 3 | 4 | 3 | 1 | 2 | 3 | 1 | 1 | 5 | 4 |
|---|
x = c(1,2,1,1,1,1,1,1,1,1,2,4,1,1)
y = c(3,3,4,3,1,2,3,1,1,5,4)
まずは図を描いてみましょう。箱ひげ図なら boxplot(x, y) です。x のほうは 1 がほとんどで，例外的に 2 と 4 があります。y のほうは中央値が 3 で，1 から 5 まで分布しています。
これらの平均値の差を $t$ 検定してみます：
t.test(x, y)
結果は次のように表示されます：
Welch Two Sample t-test
data: x and y
t = -2.9486, df = 15.916, p-value = 0.009479
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-2.3556088 -0.3846509
sample estimates:
mean of x mean of y
1.357143 2.727273
t.test() のデフォルトはWelchの方法（分散が等しいことを仮定しない $t$ 検定）です。上の出力から x の平均と y の平均がそれぞれ 1.36 と 2.73 で，これらの差の95%信頼区間が $[-2.36, -0.38]$ であることがわかります。信頼区間が 0 を含まないことから，両群の平均値の差は統計的に有意だといえます（$p = 0.009$）。
なお，分散が等しいと仮定する場合は，Rでは次のようにして計算します：
t.test(x, y, var.equal=TRUE)
結果は次のようになりました：
Two Sample t-test
data: x and y
t = -3.1158, df = 23, p-value = 0.004862
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-2.2797891 -0.4604706
sample estimates:
mean of x mean of y
1.357143 2.727273
対応するノンパラメトリックな検定としてWilcoxon-Mann-Whitney検定（分布が同じ場合）やBrunner-Munzel検定（分布が異なる場合）があります。
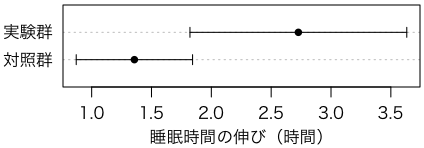
各群の95%信頼区間を比較する簡単なグラフを付けておきます。
cix = t.test(x)$conf.int
ciy = t.test(y)$conf.int
dotchart(c(mean(x),mean(y)), pch=16, xlim=range(cix,ciy),
xlab="睡眠時間の伸び（時間）")
arrows(cix[1], 1, cix[2], 1, length=0.05, angle=90, code=3)
arrows(ciy[1], 2, ciy[2], 2, length=0.05, angle=90, code=3)
mtext(c("対照群","実験群"), side=2, at=1:2, line=0.5, las=1)
Rの t.test() はデータそのものを与えますが，個数1，平均1，標準偏差1，個数2，平均2，標準偏差2を与えて等分散・非等分散の $t$ 検定をする関数は次のように書くことができます。標準偏差は $n - 1$ で割る方式であることに注意してください。
ttest = function(n1, x1, s1, n2, x2, s2) {
n = n1 + n2 - 2
u = ((n1 - 1) * s1^2 + (n2 - 1) * s2^2) / n
t = (x1 - x2) / sqrt(u / n1 + u / n2)
r = cat("Equal variance:\n\t", sep="")
r = cat(r, "t = ", t, ", df = ", n, ", p = ", 2 * pt(-abs(t), n), "\n", sep="")
t = (x1 - x2) / sqrt(s1^2 / n1 + s2^2 / n2)
n = (s1^2 / n1 + s2^2 / n2)^2 / ((s1^2 / n1)^2 / (n1-1) + (s2^2 / n2)^2 / (n2-1))
r = cat(r, "Unequal variance:\n\t", sep="")
cat(r, "t = ", t, ", df = ", n, ", p = ", 2 * pt(-abs(t), n), "\n", sep="")
}
1標本の場合，つまり片方の値が確定している場合は，確定しているほうの標準偏差を 0，個数を 2 以上の適当な数にしてください。
「分散が等しいかどうか不明のときは，分散が等しいことを仮定しない $t$ 検定（Welch の方法）を使う」というのが現在のベストプラクティスです。
次のような「2段階検定」が過去において薦められたことがありました：「等分散かどうかわからないときは，まず等分散かどうかの検定をして，その $p$ 値が0.05（あるいはそれ以外の適当な数）より大きければ等分散を仮定した $t$ 検定を行い，そうでなければ等分散を仮定しない $t$ 検定を行う」。
これは，統計的検定の基本の誤解から来ていると思われます。等分散の検定で $p$ 値が十分小さければ「等分散でない」というのはいいのですが，$p$ 値が十分小さくなければ「等分散である」というのは間違いで，「等分散かどうかかわからない」というのが統計的検定の基本です。「等分散かどうかかわからない」ときに「等分散である」を仮定した $t$ 検定を行えば，正しい結果は得られません。
$p$ 値の求め方が妥当かどうかのチェックとして，帰無仮説のもとに，多数の $p$ 値をシミュレーションで求めて，$p \leqq \alpha$ が偶然に現れる確率が $\alpha$ であるかどうか（つまり $p$ 値が区間 $[0,1]$ で一様分布かどうか）を調べることが考えられます。
「母平均が等しい」という帰無仮説を満たすデータ2組を作ります。ここでは $N(0, 1.5^2)$ に従う10個の $x$ と，$N(0,1)$ に従う30個の $y$ を使いましょう。これらの平均値の差を $t$ 検定するには
x = rnorm(10, mean=0, sd=1.5)
y = rnorm(30, mean=0, sd=1.0)
t.test(x, y)
とすればいいのですが，これを100万回行って，$p$ 値のヒストグラムを描いてみます：
p = replicate(1000000, {
x = rnorm(10, mean=0, sd=1.5)
y = rnorm(30, mean=0, sd=1.0)
t.test(x, y)$p.value
})
hist(p, freq=FALSE, col="gray")
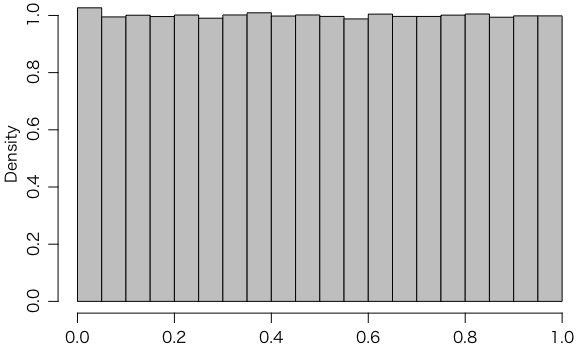
帰無仮説のもとに $p$ 値は一様分布をするはずですが，上の図は，確かにそうなっていることを示しています。
今度は，$x$ と $y$ の分散が等しいかどうかの検定 var.test(x, y) をまず行って，その $p$ 値が 0.05 より大きいときだけ，分散が等しい場合の $t$ 検定をすることにしてみましょう。
p2 = replicate(1000000, {
x = rnorm(10, mean=0, sd=1.5)
y = rnorm(30, mean=0, sd=1.0)
vp = var.test(x, y)$p.value
t.test(x, y, var.equal=(vp > 0.05))$p.value
})
hist(p2, freq=FALSE, col="gray")
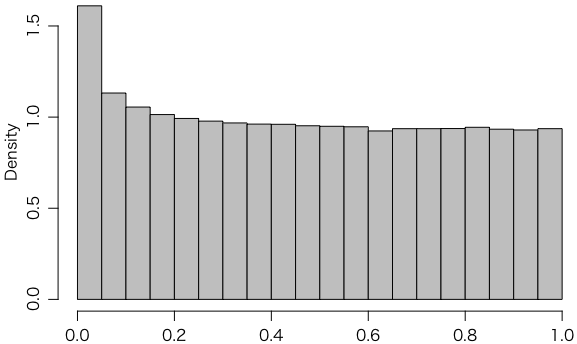
これは一様分布になっていません。このような「2段階検定」は正しい $p$ 値を与えないことになります。
念のため，SPSSの薦めるLevene（ルビーン，レビーン）検定による方法もやってみましょう。これはRでは car（Companion to Applied Regression）というパッケージに leveneTest() という名前で入っています。
install.packages("car")
library(car)
g = rep(factor(c(1,2)), c(10,30))
p3 = replicate(1000000, {
x = rnorm(10, mean=0, sd=1.5)
y = rnorm(30, mean=0, sd=1.0)
vp = leveneTest(c(x,y) ~ g, center="mean")$Pr[1]
t.test(x, y, var.equal=(vp > 0.05))$p.value
})
hist(p3, freq=FALSE, col="gray")
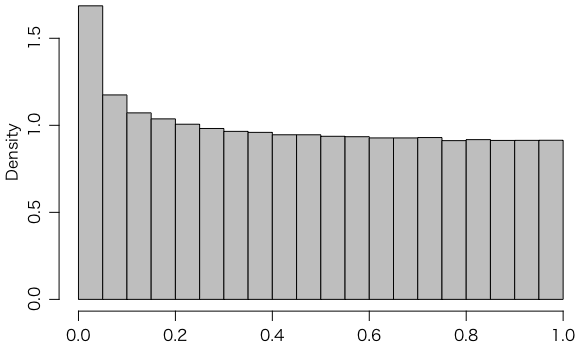
やはり一様分布になりません。ちなみに，上で使った leveneTest(..., center="mean") は平均を使う元来のLevene検定ですが，デフォルト（center="median"）は中央値を使う方法（Brown-Forsythe検定）です。
もう少し詳しく書くと，等分散を仮定した $t$ 検定でも，両群のデータ数が等しい場合は多少の分散の違いに頑健ですが，そうでない場合は，上の例のように分散が大きい群が少ないと左が上がり，逆の場合は左が下がります。これが重畳されて，上のような結果になるわけです。
なお，事前検定を行うことが不適切であることはだんだん理解されてきているので，この観点から言えば「等分散検定後に普通の t 検定」というのは好ましくない。分散が等しかろうと等しくなかろうと，最初からズバリ「等分散を仮定しない t 検定」を行うのが正しいやり方である。
たとえば $n$ 人の被験者について，ある薬を飲む前の値 $X_1$, $X_2$, ..., $X_n$ と，飲んだ後の値 $Y_1$, $Y_2$, ..., $Y_n$ を測定したとしましょう。このときは，上で述べた2標本の平均の差の検定をそのまま行うよりも，差 $d_i = X_i - Y_i$ について1標本の平均の差の検定をするほうが，一般に良い結果が得られます。
シミュレーションで確かめてみましょう。$x$ は $N(0,1)$ からの50個の乱数，$y$ はそれにさらに $N(0.2, 0.5^2)$ を加えたものです。100万回のシミュレーションで，$p \leqq 0.05$ になる確率（検出力，検定力）を調べます。
p = replicate(1000000, {
x = rnorm(50)
y = x + rnorm(50, mean=0.2, sd=0.5)
c(t.test(x,y)$p.value, t.test(x-y)$p.value)
})
mean(p[1,] <= 0.05)
mean(p[2,] <= 0.05)
t.test(x, y) で優位な結果が得られる確率は0.3%ほどしかないのに，t.test(x - y) なら79%の確率で有意になります。
このように，値が独立ではなくペアの関係があるなら，その情報を利用しないと損です。
このような，対応がある場合の $t$ 検定は，プリテスト・ポストテストの差の分析のほか，一卵性双生児を使った実験にも使われます。また，何らかの指標が似ている人どうしで人為的なペアを作るということもしばしば行われますが，その場合は，その「何らかの指標」を含めたモデル化をすることも含めて，よく検討すべきかもしれません。
なお，t.test(X - Y) の代わりに t.test(X, Y, paired=TRUE) としても同じことです。
t.test() に対応するものは oneway.test()
です。これはデフォルト（var.equal=FALSE）では
B. L. Welch (1951), On the comparison of several mean values: an alternative approach. Biometrika, 38, 330-336
に従って等分散を仮定しない検定をします。
1000人の被験者をリクルートして，ある薬が効くかどうかテストしようとしています。もし薬の効果がないなら，5%水準の $t$ 検定をすれば，間違って有意な効果があるという結果が出てしまう確率は5%のはずです。確かめてみましょう。
foo = function() {
x = rnorm(1000)
if (t.test(x)$p.value < 0.05)
return(1)
return(0)
}
a = replicate(1000, foo())
mean(a)
でも，1000人もの被験者をリクルートするのはたいへんです。最初は少人数の被験者で始めて，有意な結果が出なければ少しずつ人数を増やしていくという案を思いつきました。この場合，間違って有意な結果が出てしまう確率はどれくらいあるのでしょうか。
foo = function() {
x = rnorm(1000)
for (i in 2:1000) {
if (t.test(x[1:i])$p.value < 0.05)
return(1)
}
return(0)
}
a = replicate(1000, foo())
mean(a)
おやおや？！
Last modified: