2組の数
\[ \{ x_1, x_2, \ldots, x_n \},\quad \{ y_1, y_2, \ldots, y_m \} \]があったとき、$x_i > y_j$ を満たす $(i, j)$ の組の個数に $x_i = y_j$ を満たす組の個数の半分を足したものを $U$ とすると、もしこれらの $n + m$ 個の数の並び順がランダムであれば、$U$ の確率分布は漸化式 $p_{n,m}(U) = \frac{n}{n+m} p_{n-1,m}(U-m) + \frac{m}{n+m} p_{n,m-1}(U)$ から計算できます。さらに、$n$, $m$ が大きければ、$U$ の分布はほぼ正規分布 $N(nm/2, nm(n+m+1)/12)$ になります。このことを使った検定を、Wilcoxon-Mann-Whitney検定(ウィルコクソン・マン・ホイットニー検定、WMW検定)といいます[$U$ の定義は統計ソフトによって若干異なります]。
上で定義した $U$ の値は、$n + m$ 個の中での $x_1, x_2, \ldots, x_n$ の順位の和から $n(n + 1)/2$ を引いた値に等しいので、$U$ を使った検定は、順位和を使った検定ということもできます。
この検定は、まず American Cyanamid という会社の Wilcoxon(ウィルコクソン)という人が1945年に、1標本の場合(Wilcoxon の符号付き順位検定)と2標本の場合(この方法)の考え方を提案し、1947年に Mann(マン)と Whitney(ホイットニー)が $U$ という統計量を導入して統計学的に論じました。呼び方としては、Wilcoxon の順位和検定(Wilcoxon rank-sum test)、Mann-Whitney の $U$ 検定(Mann-Whitney $U$ test)、Wilcoxon-Mann-Whitney 検定(WMW test)、Mann-Whitney-Wilcoxon 検定(MWW test)等がありますが、どれも同じことです。
Andrew Gelman先生はWMW検定に否定的です:
Lumley (1996) のデータ (T. Lumley, Biometrics 52, 354-361) をRでWMW検定してみます。
> x = c(1,2,1,1,1,1,1,1,1,1,2,4,1,1) > y = c(3,3,4,3,1,2,3,1,1,5,4) > wilcox.test(x,y) Wilcoxon rank sum test with continuity correction data: x and y W = 32.5, p-value = 0.007741 alternative hypothesis: true location shift is not equal to 0 警告メッセージ: wilcox.test.default(x, y) で: タイがあるため、正確な p 値を計算することができません
ここで W と出ているのは $x_i > y_j$ となる $(i, j)$ の数に $x_i = y_j$ となる $(i, j)$ の数の半分を加えたものです(さきほどの $U$ の定義と逆になっています)。
さきほどWMW検定は漸化式により正確な $p$ 値が求められると書きましたが、この場合はタイ(等しい値)があるので、漸化式は使えず、正規分布による近似値になってしまったようです。タイがなくても、両群の個数の和が50以上になると、正規分布近似に切り替わるので、50個以上の場合に正確な値を求めたいなら wilcox.test(x,y,exact=TRUE) とすればいいのですが、タイが一つでもあれば、このオプションを付けても無駄です。正確な値を求めたければ、exactRankTests というパッケージを使うのが一つの方法です。
> library(exactRankTests) Package ‘exactRankTests’ is no longer under development. Please consider using package ‘coin’ instead. > wilcox.exact(x,y) Exact Wilcoxon rank sum test data: x and y W = 32.5, p-value = 0.00669 alternative hypothesis: true mu is not equal to 0
メッセージにも出ていますが、exactRankTests パッケージは開発が継続されていないようです。代わりに coin パッケージを使えということですので、やってみましょう。使い方がちょっと違います。
library(coin)
wilcox_test(c(x,y) ~ factor(c(rep("x",length(x)),rep("y",length(y)))),
distribution="exact")
結果は wilcox.exact(x,y) と同じになります。
WMW検定は両群がまったく同じ分布をしているという帰無仮説の検定です。実質的には順位を $t$ 検定しているのとほぼ同じことですので、両群の分散が異なる場合は、順位に直して、等分散を仮定しない $t$ 検定をするという手が考えられます(次節参照。より最近の方法としてはBrunner-Munzel検定があります)。$t$ 検定の前に順位に直すことは、外れ値に対して頑健になるという意味がありますが、このLumleyのデータのように5点法で評価した値などは外れ値の心配はありませんし、タイが多いので順位は不自然になりますので、t検定で示したように5点法の点数そのままでWelchの検定(分散が等しいことを仮定しない $t$ 検定)を使う方が、信頼区間も出せて使い勝手が良いと思います。
WMW検定は、$x_i > y_j$ を満たすペアの個数についての検定だといえばもっともらしく聞こえますが、各群の順位和についての検定だというと、間隔尺度でない順位を合計して何の意味があるのだ!と叱られるかもしれません。実際にはどちらの言い方も数学的に同値です。

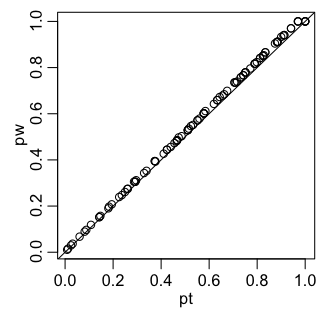
WMW検定と、分散が等しいと仮定する $t$ 検定を順位について適用した場合とでは、ほぼ同じことを調べているので、両者の $p$ 値はほぼ一致します(右図)。
この図は次のRのプログラムで描きました:
r = replicate(100, {
a = sample(20)
b = sample(5:10, 1)
x = a[1:b]
y = a[(b+1):20]
c(t.test(x, y, var.equal=TRUE)$p.value, wilcox.test(x, y)$p.value)
})
plot(r[1,], r[2,], xlab="pt", ylab="pw", asp=1)
abline(0, 1)
すでに述べたように、この検定は2群の分布が等しいときに意味があります。例えば分散が異なると、正しくない結果を与えます。t検定のときと同様にチェックしてみましょう。
p = replicate(1000000, {
x = rnorm(10, mean=0, sd=1.5)
y = rnorm(30, mean=0, sd=1.0)
wilcox.test(x, y)$p.value
})
hist(p, freq=FALSE, col="gray")
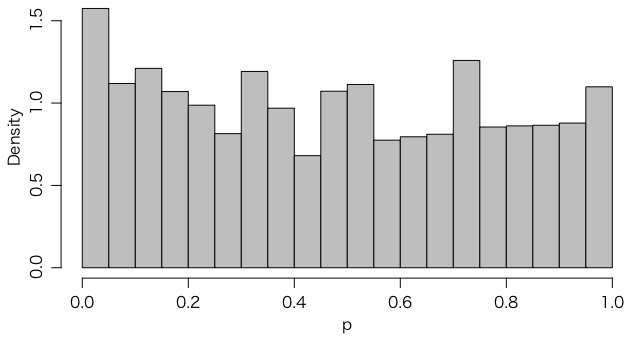
ノンパラメトリック検定はこのように小サンプルではぎざぎざになることが多いので、各群のサンプルサイズを10倍にしてみましょう。
q = replicate(1000000, {
x = rnorm(100, mean=0, sd=1.5)
y = rnorm(300, mean=0, sd=1.0)
wilcox.test(x, y)$p.value
})
hist(q, freq=FALSE, col="gray")
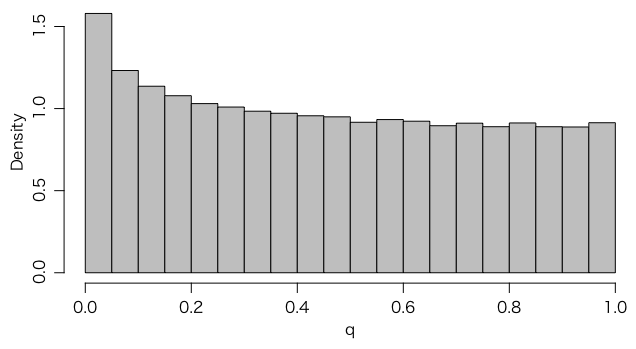
このように、$p < 0.05$ のところが多く出すぎてしまいます。