40個の正規分布の乱数を2組作って,それぞれを横軸,縦軸にとってプロットしてみましょう:
x = rnorm(40); y = rnorm(40); plot(x, y)
デフォルトの白丸では見にくいので,黒丸(pch=16)にしましょう:
x = rnorm(40); y = rnorm(40); plot(x, y, pch=16)
これから勉強する「相関係数」を上に書き加えてみましょう:
x = rnorm(40); y = rnorm(40); plot(x, y, pch=16, main=cor(x,y))
何度もやって,感覚をつかみましょう。
2008年9月24日に就任した中山成彬(なりあき)国土交通相は,「日教組(日本教職員組合)が強いところは学力が低い」などの発言で,5日後の28日には辞職してしまいます。
この「日教組が強いところは学力が低い」を反証するため,朝日新聞は27日朝刊で13道府県の全国学力調査の中3数学Aの点数をもとに「相関なし」と結論づけています。しかし,この13道府県はどういう基準で選んだのか,なぜ中3数学Aなのか,疑問の残る記事になってしまいました。紙面には「〈注〉科目は1位と最下位の県の得点差が最も大きいものを選びました」とありますが,恣意的に特定の科目を選んだととられないためには,全科目を調べるか,あるいは総合得点を使うべきでした。
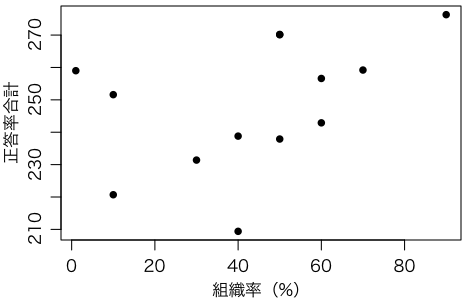
同じ朝日新聞でも,版によっては13道府県の日教組組織率を数字で挙げています。文科省サイトで公開されている平成20年度全国学力・学習状況調査の都道府県別の全4科目正答率の合計と合わせて表にしておきます。組織率データの信頼性については,ここでは不問とします。

| 組織率(%) | 正答率合計 | |
|---|---|---|
| 北海道 | 50 | 237.9 |
| 岩手県 | 40 | 238.8 |
| 秋田県 | 50 | 270.2 |
| 富山県 | 50 | 270.1 |
| 福井県 | 90 | 276.3 |
| 静岡県 | 70 | 259.2 |
| 愛知県 | 60 | 256.6 |
| 大阪府 | 30 | 231.4 |
| 香川県 | 1 | 259.0 |
| 高知県 | 10 | 220.7 |
| 大分県 | 60 | 242.9 |
| 宮崎県 | 10 | 251.6 |
| 沖縄県 | 40 | 209.4 |
このデータの散布図(相関図)を描いてください。Rなら次のコマンドで描けます。
組織率 = c(50,40,50,50,90,70,60,30,1,10,60,10,40)
正答率合計 = c(237.9,238.8,270.2,270.1,276.3,259.2,256.6,231.4,259.0,220.7,242.9,251.6,209.4)
plot(組織率, 正答率合計)
実際には次のように多少オプションを付けて描きました:
par(mgp=c(2,0.8,0))
plot(組織率, 正答率合計, pch=16, xlab="組織率(%)")
実際に描いてみると,なんとなく右肩上がりに見えるかもしれません。この傾向の度合,つまりこの場合は組織率と正答率合計の関連の度合を数字にしたものが,相関係数(correlation coefficient,長い名前はピアソンの積率相関係数 Pearson's product-moment correlation coefficient)です。相関係数は -1 から 1 までの値をとり,正負の関連が強いほど ±1 に近づき,関連が低ければ 0 に近づきます(詳しくは後で述べます)。
上のピアソンは Karl Pearson(1857〜1936年)ですが,その息子 Egon S. Pearson(1895〜1980年)もネイマン・ピアソンの理論で有名です。
Rで相関係数を求める関数は cor() です。
cor(組織率, 正答率合計)[1] 0.4251695
$p$ 値や信頼区間まで求める関数は cor.test() です:
cor.test(組織率, 正答率合計)Pearson's product-moment correlationdata: 組織率 and 正答率合計t = 1.558, df = 11, p-value = 0.1475alternative hypothesis: true correlation is not equal to 095 percent confidence interval:-0.1643066 0.7908813sample estimates:cor0.4251695
つまり,(ピアソンの)相関係数は 0.425 で,組合の組織率が高いほど成績が良いという傾向が見られますが,95%信頼区間は $[-0.16, 0.79]$ と広く($p$ 値は 0.15 ほど),統計的に有意ではありません。したがって,このデータから何かを結論づけるのは早計です。
いずれにしても,47都道府県からこの13道府県を選んだ理由が明らかでありませんので(もしかしたら朝日新聞が恣意的に選んだ?),もともと何の意味もないデータといえます。
もし47都道府県全部のデータがあったとしても,人口1千万の東京都と人口数十万の小さな県を同じ重みで考えていいのかという疑問もあります。県ごと(あるいは国ごと)のデータを散布図にすると何らかの知見が得られることはよくありますが,相関係数から量的な結論を導く際には注意が必要です。
仮に相関関係が見られた場合でも,それを因果関係と結びつけるのは早計です。例えば「組合が強いところは学力が低い」という相関関係が見られたとしても(このデータからは逆の関係が示唆されていますが),それだけでは,組合が学力を下げているとも,学力が低いから組合でがんばっているともいえますし,まったく別の要因が両方の原因となっているのかもしれません。
要は,相関関係から安易に因果関係を導いてはいけないということです。
上のようなプロットを描くと,右上がりの直線を書き足したくなりますね。このようなデータを直線で近似するのが回帰分析(regression analysis)の考え方です。なぜ「回帰」(regression,元に戻ること)というかは後で説明します。
上のようなプロットにどうやって「えいやっ」と直線を引くかは,通常は,直線と点との鉛直距離の2乗の和を最小にする「最小2乗法」を使います。そのためのRの関数が lm() です(linear modelから来ています)。
r = lm(正答率合計 ~ 組織率)abline(r)# 上で描いたプロットに直線を重ね書きするsummary(r)Call:lm(formula = 正答率合計 ~ 組織率)Residuals:Min 1Q Median 3Q Max-37.551 -12.200 2.197 14.701 25.116Coefficients:Estimate Std. Error t value Pr(>|t|)(Intercept) 233.5486 10.6703 21.888 2.03e-10 ***組織率 0.3351 0.2151 1.558 0.148---Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1Residual standard error: 18.98 on 11 degrees of freedomMultiple R-squared: 0.1808, Adjusted R-squared: 0.1063F-statistic: 2.427 on 1 and 11 DF, p-value: 0.1475
これは,正答率合計 = 0.3351 × 組織率 + 233.5486 という式で予測できることを示しています。ただし,$p$ 値はさきほどと同じ 0.1475 です。相関係数が 0 であるという帰無仮説と,回帰分析したとき傾きが 0 であるという帰無仮説とは,同じことだからです。
後で使うために係数だけ取り出したい場合は coef() 関数を使います(r$coefficients でも同じです):
coef(r)(Intercept) 組織率233.54856 0.33506
係数の信頼区間は confint() 関数で取り出せます:
confint(r)2.5 % 97.5 %(Intercept) 210.0633470 257.0337801組織率 -0.1382923 0.8084123
ほかに predict() 関数や residuals() 関数,rstudent() 関数も便利です。plot() は4通りの診断プロットを出力します。4通りを1枚にまとめるには par(mfrow=c(2,2)); plot(r) とします。
「準備体操」のプロットに直線をあてはめてみましょう:
x = rnorm(40); y = rnorm(40); plot(x, y, pch=16, main=cor(x,y)); abline(lm(y ~ x))
何度もやって感覚をつかみましょう。
横軸が中間試験の成績,縦軸が期末試験の成績とすると,相関が完全でないために,中間試験で良い点をとった人でも,期末試験では平均(0)に近くなります。
横軸が親の成績,縦軸が子の成績とすると,相関が完全でないために,親が優秀でも,子は平均(0)に近くなります。
この現象が,有名なフランシス・ゴルトンが発見した「平均への回帰」(regression to the mean)です。
相関係数と名の付くものは上のピアソンの相関係数以外にもいくつかあり,Rでは後述のケンドールの順位相関係数,スピアマンの順位相関係数が同じ cor() で計算できます:
cor(組織率, 正答率合計, method="kendall")[1] 0.3736324cor(組織率, 正答率合計, method="spearman")[1] 0.5076522
$p$ 値や信頼区間まで求める関数はやはり cor.test() です:
cor.test(組織率, 正答率合計, method="kendall")Kendall's rank correlation taudata: 組織率 and 正答率合計z = 1.7298, p-value = 0.08366alternative hypothesis: true tau is not equal to 0sample estimates:tau0.3736324Warning message:In cor.test.default(組織率, 正答率合計, method = "kendall") :タイのため正確な p 値を計算することができませんcor.test(組織率, 正答率合計, method="spearman")Spearman's rank correlation rhodata: 組織率 and 正答率合計S = 179.2146, p-value = 0.07656alternative hypothesis: true rho is not equal to 0sample estimates:rho0.5076522Warning message:In cor.test.default(組織率, 正答率合計, method = "spearman") :タイのため正確な p 値を計算することができません
このどれもが $p \leq 0.05$ を満たしていません(有意な結果が得られるようにいろいろな計算法を試すのはいけないことですが)。
以下ではこれらの相関係数についてさらに詳しく説明します。
互いに関連する(独立でない)二つの確率変数 $X$,$Y$ を考えます。例えば $X$ は数学の点数,$Y$ は理科の点数だとすると,$X$ が平均より大きいときは $Y$ も平均より大きい傾向があり,$X$ が平均より小さいときは $Y$ も平均より小さい傾向がありそうです。このような二つの変数の間の関係を調べてみましょう。
平均よりどれくらい大きいか(小さいか)を調べるには,テストの点数なら偏差値に直すほうがわかりやすいでしょう。同じように,統計学でも,変数 $X$ の平均値(期待値)を $\mu_X = E(X)$,分散を $\sigma_X^2 = E((X - \mu_X)^2)$ とするとき,
\[ x = \frac{X - \mu_X}{\sigma_X} \]で与えられる $x$ に変換して考えると便利なことがあります。$X$ を $x$ に直すことを標準化する(standardize)ということにします。同様に $Y$ を標準化したものを $y$ とします。
こうしておくと,
\[ E(x) = 0, \quad E(x^2) = 1, \quad E(y) = 0, \quad E(y^2) = 1 \]となります。
ここでもし $X$,$Y$ が独立なら積の期待値は $E(xy) = 0$ ですが,一般には $E(xy)$ は必ずしも 0 になりません:
この
\[ \rho = E(xy) = E\biggl(\frac{X - \mu_X}{\sigma_X} \cdot \frac{Y - \mu_Y}{\sigma_Y}\biggr) \]が,$X$ と $Y$ の相関係数(ピアソンの積率相関係数)です。証明は省きますが,相関係数 $\rho$ は必ず
\[ -1 \leq \rho \leq 1 \]の範囲に入ります。
上の $\rho$ は母集団 $X$,$Y$ の相関係数でしたが,標本については
\[ \begin{align*} r &= \frac{1}{n-1} \sum_{i=1}^n \frac{X_i - \bar{X}}{s_X} \frac{Y_i - \bar{Y}}{s_Y} \\ &= \frac{\displaystyle \frac{1}{n-1} \sum_{i=1}^n (X_i - \bar{X})(Y_i - \bar{Y})}{\displaystyle \sqrt{\frac{1}{n-1} \sum_{i=1}^n (X_i - \bar{X})^2} \sqrt{\frac{1}{n-1} \sum_{i=1}^n (Y_i - \bar{Y})^2}} \end{align*} \]で計算します。この最後の式では $1/(n-1)$ はすべて約分して消すことができますので,「$n$ で割るか $n - 1$ で割るか」の話はここでは影響しません。この $r$ も必ず $-1 \leq r \leq 1$ の範囲に入ります。
数学的には,$r$ は二つの $n$ 次元の単位ベクトルの内積にほかならず,このことがわかれば $-1 \leq r \leq 1$ は自明です((コーシー・)シュワルツの不等式)。
この最後の式の分子 $\displaystyle \frac{1}{n-1} \sum_{i=1}^n (X_i - \bar{X})(Y_i - \bar{Y})$ を $X$ と $Y$ の共分散(covariance)と呼びます。
Rで例えば $X_1 = 1$, $X_2 = 2$, $X_3 = 3$ と $Y_1 = 1$, $Y_2 = 3$, $Y_3 = 2$ の相関係数を求めるには,次のようにします。
x = c(1,2,3)# x = 1:3 でも同じy = c(1,3,2)cor(x, y)
これで $r = 0.5$ が求まります。
$X$,$Y$ が独立に正規分布に従うなら,
\[ t = \frac{r \sqrt{n-2}}{\sqrt{1 - r^2}} \]は自由度 $n - 2$ の $t$ 分布に従います。
さきほどの例で計算すると,
x = c(1, 2, 3)# x = 1:3 でも同じy = c(1, 3, 2)r = cor(x, y)# r = 0.5 になるn = 3t = r * sqrt(n-2) / sqrt(1 - r^2)# t = 0.57735032 * pt(-t, n-2)# 0.6666667 と表示される
となります。より簡単には cor.test(x, y) と打ち込めば相関係数と $p$ 値などが出力されます。
cor.test(x, y)Pearson's product-moment correlationdata: x and yt = 0.5774, df = 1, p-value = 0.6667alternative hypothesis: true correlation is not equal to 0sample estimates:cor0.5
相関係数 $r$ の不偏推定量 $G(r)$ は次の式で近似できます(Ingram Olkin and John W. Pratt, ``Unbiased Estimation of Certain Correlation Coefficients'', The Annals of Mathematical Statistics, Vol.29, No.1 (1958), pp.201-211.)。
\[ G(r) = \left( 1 + \frac{1 - r^2}{2(n - 3)} \right) r\]この式の誤差は $n \geq 8$ で 0.01 以下,$n \geq 18$ で 0.001 以下とのことです。
共分散を求めるRの関数は cov() です。なお,高校数学では,分散も共分散も,分母が $n-1$ でなく $n$ のものを使いますので,Rの分散 var(),共分散 cov() の結果と異なります。Excelについては,古くは $n$ で割る方式の COVAR() がありましたが,Excel 2010以降は $n$ で割る方式の COVARIANCE.P() と,$n-1$ で割る方式の COVARIANCE.S() があるようです。
共分散には $\mathrm{cov}(X+Y,Z) = \mathrm{cov}(X,Z) + \mathrm{cov}(Y,Z)$ という線形性があります。特に $X+Y=Z$ のとき $\mathrm{cov}(X,Z) + \mathrm{cov}(Y,Z) = \mathrm{cov}(Z,Z) = \mathrm{var}(Z)$ ですので,$\mathrm{cov}(X,Z)/\mathrm{var}(Z) + \mathrm{cov}(Y,Z)/\mathrm{var}(Z) = 1$ になります。この左辺の各項を $X$ と $Y$ の共分散比と呼ぶことがあります。共分散比の合計は 1 です。例えば $X$ をセンター試験の点数,$Y$ を個別試験の点数とすると,共分散比は各試験の寄与率を表すと考えられます。共分散比は試験の数が3個以上でも定義できますので,各試験科目の寄与率を求めるのにも共分散比が使われます。
ピアソンの積率相関係数は,外れ値に影響されやすいという欠点があります。そのため,データの数値そのものではなく,その順位だけによる方法がいくつか考えられました。
一つは,単にデータの順位からピアソンの相関係数を求める方法です。この方法による相関係数を,スピアマンの順位相関係数またはスピアマンの $\rho$(ロー)(Spearman's rank correlation coefficient,Spearman's rho)といいます。
等しい値(タイ,tie)が現れるときは,その順位は,等しくなかったときの順位の平均値にします。たとえば,実際の値が 5, 7, 7, 9, 10 のとき,順位は 1, 2.5, 2.5, 4, 5 とします(あるいは大きい順に 5, 3.5, 3.5, 2, 1 としても同じことです)。
スピアマンの $\rho$ の検定は,$n$ が十分大きければピアソンの相関係数と同じ方法($t$ 検定)で可能です。
Rの cor.test(..., method="spearman") で,帰無仮説を $\rho = 0$ としたときのスピアマンの $\rho$ の検定は,$n \leq 1290$ のときは D. J. Best and D. E. Roberts, ``Algorithm AS 89: The Upper Tail Probabilities of Spearman's Rho,'' Applied Statistics, Vol.24, No.3 (1975), pp.377-379 にほぼ従って計算します。これは,$n \leq 9$(元論文では 6)のときは片方のデータの $n!$ 通りの並べ替えを行って,そのうち何通りが,観測された $|\rho|$ 以上の値をとるかを調べ,それを $n!$ で割ったものを求めます。$n > 9$(元論文では $n > 6$)のときは $1/n$ についての級数展開で,少なくとも2桁の精度があるとのことです。$n > 1290$ のときは $t$ 検定を使います。
もう一つのよく使われるものは,ケンドールの順位相関係数またはケンドールの $\tau$(タウ)(Kendall's rank correlation coefficient,Kendall's tau)と呼ばれるものです。ケンドールが1938年に流行らせたのでこう呼ばれますが,ケンドールによれば,1900年ごろからいろいろな人が使っていたとのことです。
これの求めようとするものは,ランダムに二つを選んだとき,その $X$ の順序と $Y$ の順序が同じになる確率(例えば,A君がB君より数学ができたとき,A君がB君より英語もできる確率)です。実際には,この確率を2倍して1を引くことにより,-1 から 1 の範囲に収めたものが,ケンドールの $\tau$ です。スピアマンの $\rho$ より具体的に求めようとしているものがはっきりしているのと,正規分布で近似しやすいことが特長です。
より具体的には,すべてのペアについて,両変数が同順のペアの数から逆順のペアの数を引き,ペアの総数 $n(n-1)/2$ で割ったものがケンドールの $\tau$ です。タイがある場合も含めてもっと厳密にいうと,$S = m_x = m_y = 0$ を初期値として,$1 \leq i < j \leq n$ を満たすすべての整数のペア $(i,j)$ について,
を行い,最後に
\[ \tau = \frac{S}{\sqrt{\vphantom{m} \smash{m_x m_y}}} \]とすると $\tau$ が求まります。分子 $S$ は同順のペア数から逆順のペア数を引いたもので,分母は基本的にはペアの総数 $m = n(n-1)/2$ ですが,タイがある場合は各変数のタイでないペアの総数の相乗平均としています。
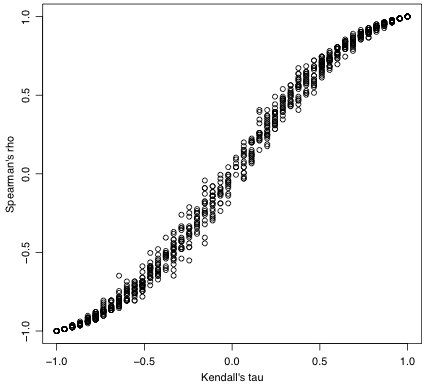
ケンドールの $\tau$ とスピアマンの $\rho$ は,いずれも -1 から 1 までの値をとり,二つの変数の順序関係がまったく同順であれば 1,まったく逆順であれば -1 になるという点では同じです。両者に1対1の対応はありませんが,近似的に非線形な関係があり,中程度の相関では $\tau$ のほうが絶対値が小さくなります。どちらが統計的に有意になりやすいということはありません。$\tau$ のほうが正規分布に近いので扱いやすい反面,$n$ が小さいと $\tau$ は $\rho$ に比べて飛び飛びの値しか取らないことが目立ちます。
下の図は10ペアの乱数を何回も作ってケンドールの $\tau$(横軸)とスピアマンの $\rho$(縦軸)を計算した結果の散布図です。
2変数が同じ順に並んでいても,タイの位置が異なれば,どちらの順位相関係数も 1 になりません。
ケンドールの $\tau$ のタイの処理の仕方はいくつか考えられますが,上で述べたものは $\tau_b$ と呼ばれる方法です。Rでは $\tau_b$ が使われます。
Rの cor.test(..., method="kendall") で,帰無仮説を $\tau = 0$ としたときのケンドールの $\tau$ の検定は,$n < 50$ またはオプション exact=TRUE 指定時には,タイがなければ厳密な方法を使います。これ以外の場合は正規分布で近似する方法で行います。$\tau$ の分子 $S$ が単なる $\pm 1$ の和であることを考えれば,$n$ が大きければ中心極限定理により正規分布に近づくことが理解できます。具体的には母集団が独立のとき $\tau$ はタイがなければ正規分布 $N(0, (4n+10)/9n(n-1))$ に近づきます。
タイがある場合は cor.test(..., method="kendall") では $\tau$ の分子 $S$ が分散
の正規分布に近づくことを使っています。ここで
\[ T_k = \sum t_k (t_k - 1), \quad U_k = \sum t_k (t_k - 1) (t_k - 2), \quad V_k = \sum t_k (t_k - 1) (2 t_k + 5) \]です($k = x, y$ で,$t_x$, $t_y$ はそれぞれ $X$, $Y$ の個々のタイの長さのベクトルです。例えば $X = (1, 2, 3, 3, 4, 5, 5, 5)$ なら,$t_x = (2, 3)$ で,$\sum t_x (t_x - 1) = 2(2-1) + 3(3-1) = 8$ となります)。
タイのある場合も含めて正確な $p$ 値を求めるには,並べ替え検定の考え方を使います。例えば1万回のシミュレーションでは
t = cor(X, Y, method="kendall")
a = replicate(10000, cor(X,sample(Y),method="kendall"))
mean(abs(a) >= abs(t)) # 両側確率
このページの最初に挙げた例では $p = 0.08366$ でしたが,100万回のシミュレーションでは $p = 0.095$ ほどです。ただし,気をつけなければならないのは,ケンドールの $\tau$ が飛び飛びの値をとることです。このため,値をコピー&ペーストして使っても四捨五入のために正しくない結果を生じることがあります:
t[1] 0.3736324mean(abs(a) >= t)[1] 0.095084mean(abs(a) >= 0.3736324)[1] 0.07212mean(abs(a) >= 0.3736323)[1] 0.095084
この場合は $p = 0.095$ のほうが正しいのですが,少しずらすと $p = 0.072$ になります。正規分布による近似 $p = 0.08366$ はこのほぼ真ん中の値になっています。ちなみに,100万個の中にユニークな値は67個しかありません:
length(unique(a))[1] 67
その他の相関係数