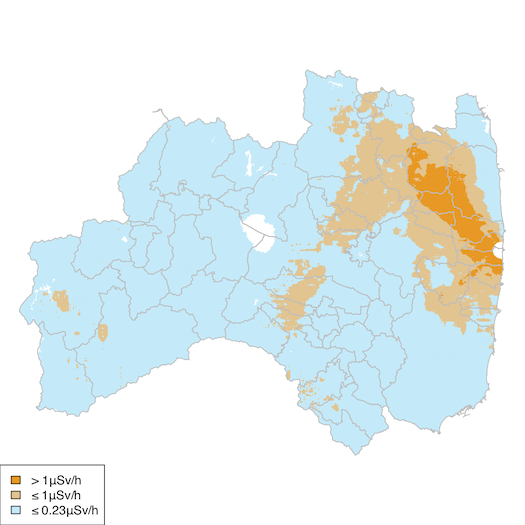
図は航空機モニタリングにより推定された2017年(平成29年)11月16日時点の福島県の空間放射線量率の分布である。

図からわかるように,除染が進み,かなりの領域(空色)で目標値0.23μSv/h以下が達成されている。なお,航空機モニタリングは600m程度の解像度しかないので,居住地周辺できめ細かな除染が行われていたり,セシウムの保持力が低い人工物の影響があったりして,居住地ではさらに線量率が低い傾向があるかもしれない。これを示すために,同じ場所のリアルタイム線量測定システムやモニタリングポストと比較した図を,このページの下のほうに載せた。
この0.23μSv/hという値は,次のようにして算出されたものである。事故による追加被曝線量を年1mSv(1000μSv)以下にするためには,1時間あたり 1000÷365÷24 ≒ 0.114 μSv以下にする必要がある。1日のうち8時間を屋外,16時間を木造屋内で過ごし,屋内での線量率は屋外の0.4倍とすると,平均して空間線量の (8 + 0.4×16) / 24 = 0.6 倍を被曝することになる。0.114÷0.6 = 0.19 であるので,空間線量が0.19μSv/h以下ならこの条件を満たすことができる。もともとあった自然放射線の量を0.04μSv/hとすれば,合計して0.23μSv/h以下にすればよいことになる。
この空間線量の0.6倍を個人線量とする見積もりは過大であり,実際の追加被曝の中央値はこれよりかなり少ないという研究がいくつかある。Miyazaki and Hayano [1] は空間線量の0.15倍(中央値)が個人線量であるとするが,不同意データが含まれていることが明らかになり,撤回(retract)される可能性がある(この線量を積分した第2論文 [2] にはさらに計算間違いもある)。Naito ほか [3] は屋内0.14倍,屋外0.32倍,Naito ほか [4] は屋内0.13倍,屋外0.18倍としている。ただし,個人差は大きい。
以下では,Rでこのような図を描く方法を説明する。
地図はシェープファイルを読むで説明した方法で描く。具体的には,国土数値情報サイトの「行政区域」から福島県を選ぶ。簡単な質問に答えるとダウンロードできる。ファイル名 N03-180101_07_GML.zip である。これを展開すると N03-180101_07_GML というフォルダの中にいくつかのファイルができる。これをRで読んで,まずは白地図を描いてみよう:
library(sf) # あらかじめsfパッケージをインストールしておく
options(stringsAsFactors=FALSE) # 文字列っぽいものは「ファクター」ではなく「文字列」として扱う
fukushima = st_read("N03-180101_07_GML/", options="ENCODING=CP932") # シェープファイルを読む
par(mar=c(0,0,0,0)) # 地図を描く場合は余白をゼロにする
plot(st_geometry(fukushima)) # 福島県の白地図が描かれる
放射線のデータは,放射性物質モニタリングデータの情報公開サイトから取得する。具体的には,空間線量率→航空機モニタリング→放射性物質の分布状況等調査による航空機モニタリング→データダウンロード→H29.11.16→CSV(UTF-8)→福島県のメッシュデータをダウンロードし,解凍してCSVファイルを取り出す。項目は
となっている。これをまずRで読む:
mesh = read.csv("1010301015_07.csv", fileEncoding="UTF-8")
空間線量率は,table(mesh[,8]) と打ち込んでみればわかるように,<1.0E-01,1.0E-01 のような文字列として読み込まれる。ここでは < を含むものは 0 とみなして数値化することにする:
mesh[,8] = as.numeric(ifelse(grepl("<",mesh[,8]), "0", mesh[,8]))
冒頭の図は次のようにして描いた:
plot(st_geometry(fukushima), border="gray")
rect(mesh[,15], mesh[,14], mesh[,11], mesh[,10], border=NA,
col=ifelse(mesh[,8] <= 0.23, "#b4ebfa",
ifelse(mesh[,8] <= 1, "#edc58f", "#ff9900")))
plot(st_geometry(fukushima), border="gray", add=TRUE)
par(family="Helvetica")
legend("bottomleft",
legend=c("> 1μSv/h","≤ 1μSv/h","≤ 0.23μSv/h"),
fill=c("#ff9900","#edc58f", "#b4ebfa"))
例えば伊達市周辺に限るなら,次のようにする:
date = subset(fukushima, N03_004=="伊達市")
plot(st_geometry(date))
rect(mesh[,15], mesh[,14], mesh[,11], mesh[,10], border=NA,
col=ifelse(mesh[,8] <= 0.23, "#b4ebfa",
ifelse(mesh[,8] <= 1, "#edc58f", "#ff9900")))
plot(st_geometry(fukushima), add=TRUE)
par(family="Helvetica")
legend("bottomleft",
legend=c("> 1μSv/h","≤ 1μSv/h","≤ 0.23μSv/h"),
fill=c("#ff9900","#edc58f", "#b4ebfa"), bg="white")
色のグラデーションを使うには,例えば次のようにする:
cols = colorRamp(c("white","#ff2800"))
plot(st_geometry(date))
rect(mesh[,15], mesh[,14], mesh[,11], mesh[,10], border=NA,
col=rgb(cols(pmin(pmax(mesh[,8]-0.09,0),1))/255))
plot(st_geometry(fukushima), add=TRUE)
周辺を消して伊達市だけにするには次のようにする:
datemesh = subset(mesh, 市町村=="伊達市")
plot(st_geometry(date))
rect(datemesh[,15], datemesh[,14], datemesh[,11], datemesh[,10], border=NA,
col=rgb(cols(pmin(pmax(datemesh[,8]-0.09,0),1))/255))
plot(st_geometry(date), add=TRUE)
航空機モニタリングと,地上1mのリアルタイム線量測定システム・モニタリングポストの値とを,比較してみよう。
地上1mの線量率は放射性物質モニタリングデータ→空間線量率→モニタリングポスト・リアルタイム線量計→全国及び福島県の空間線量測定結果(日次平均値)のデータダウンロードで,期間が重なる「全国及び福島県の空間線量測定結果(リアルタイム配信)日次平均値 ( H29.4~H30.3 )」の「福島県」をダウンロードし,解凍する。たくさんのCSVファイルが出てくる。それらを 1010403007_07 というフォルダに入れる。また,リアルタイム線量測定システムとモニタリングポストを区別するために,jsdfq43wtrさんの mp-maker-memo.csv に掲載されているものと位置情報が同じならモニタリングポストと判断する。
mplist = read.csv("mp-maker-memo.csv", header=FALSE, fileEncoding="UTF-8")
files = dir(path="1010403007_07", pattern="*.csv", full.names=TRUE, recursive=TRUE)
n = length(files)
lat = lon = rad = avi = mp = rep(NA, n)
for (i in 1:n) {
a = read.csv(files[i], fileEncoding="UTF-8")
a = subset(a, 測定日 >= "2017-11-01" & 測定日 <= "2017-11-30") # 2017年11月分を抜き出す
if (dim(a)[1] == 0) next # 空であれば次に
lat[i] = mean(a[,5])
lon[i] = mean(a[,6])
rad[i] = mean(a[,8]) # 1ヶ月分の平均線量率
d = (lat[i] - mesh[,5])^2 + (lon[i] - mesh[,6])^2
k = which.min(d) # 最近接のメッシュ点を探す
avi[i] = mesh[k,8] # メッシュ点の航空機データ
d = (lat[i] - mplist[,8])^2 + (lon[i] - mplist[,7])^2
k = which.min(d) # 最近接のモニタリングポストを探す
mp[i] = (d[k] < 0.00001)
}
plot(avi[!mp], rad[!mp], log="xy", xlim=c(0.0297,17), ylim=c(0.0297,17), asp=1, xlab="航空機モニタリング", ylab="地上1m") # リアルタイム線量測定システム
points(avi[mp], rad[mp], pch=4, col="#ff2800") # モニタリングポスト
abline(0, 1)
curve(0.7*x, col="gray", add=TRUE)
curve(0.5*x, col="gray", add=TRUE)
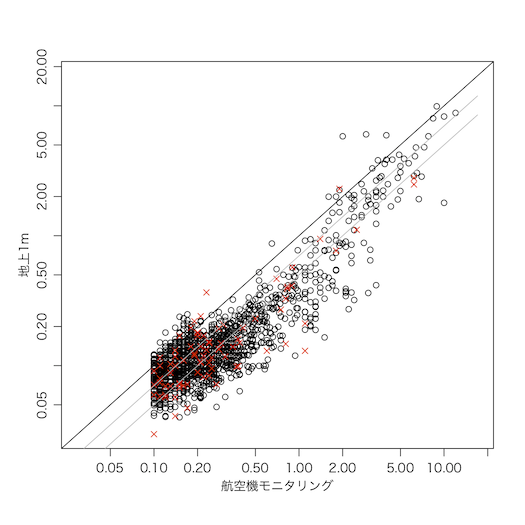
灰色の直線は航空機モニタリングの0.7倍,0.5倍を示す。航空機モニタリングに比べて地上の線量が小さいことがわかる。
ランダムな位置における地上の測定と航空機の測定が平均的に同じ値を与えるように航空機モニタリングはキャリブレートされているので,直径600mの円(航空機モニタリングの解像度)内で比較的線量の低いところに地上の測定器が設置されているという選択バイアスであることが考えられる。
あまり意味があるか疑問であるが,地上 / 航空機 の比の累積分布を描いてみよう:
avi = ifelse(avi==0, NA, avi) # 0の値はNAに変える
plot(ecdf(rad/avi), log="x", xlim=range(rad/avi, na.rm=TRUE), xlab="地上/航空機", ylab="累積割合", main="")
m = median(rad/avi, na.rm=TRUE) # 中央値0.5714286
segments(m, -0.1, m, 0.5)
segments(0.01, 0.5, m, 0.5)
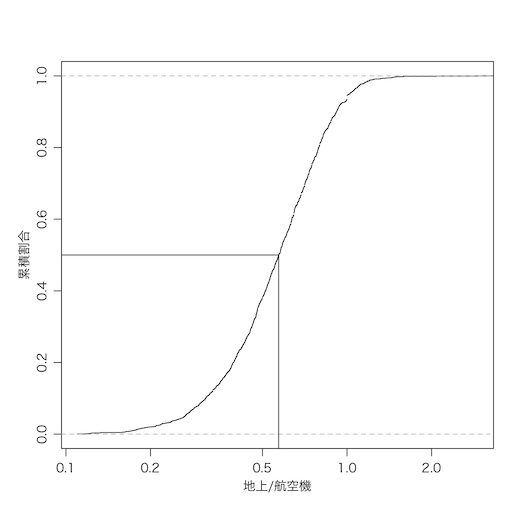
中央値 m は 0.57 ほどである。
この図の縦軸を正規分布の分布関数の逆で変換した図(対数正規分布なら直線になる):
x = na.omit(rad/avi)
p = c(0.001,0.01,0.1,0.5,0.9,0.99,0.999)
q = c(0.1,0.2,0.5,1,2)
n = length(x)
plot(sort(x), qnorm((1:n)/n), type="s", xlab="ground/airborne", ylab="cumulative prob.",
log="x", xaxt="n", yaxt="n", xlim=c(0.1,2), ylim=qnorm(c(0.0005,0.9995)),
panel.first=abline(h=qnorm(p),v=q,col="lightgray"))
axis(2, qnorm(p), p)
axis(1, q, q)
m = median(x) # 0.5714286
segments(m, -4, m, 0, col="lightgray")
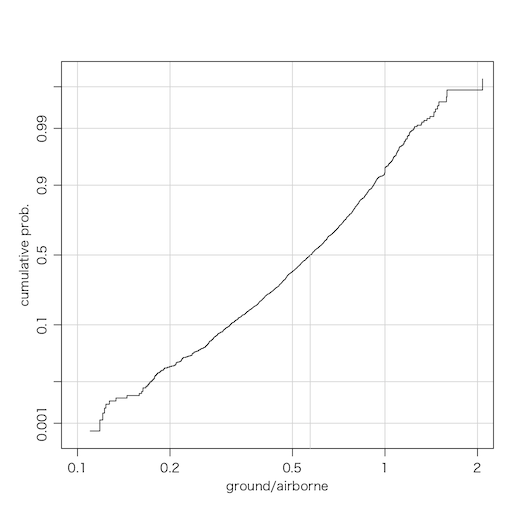
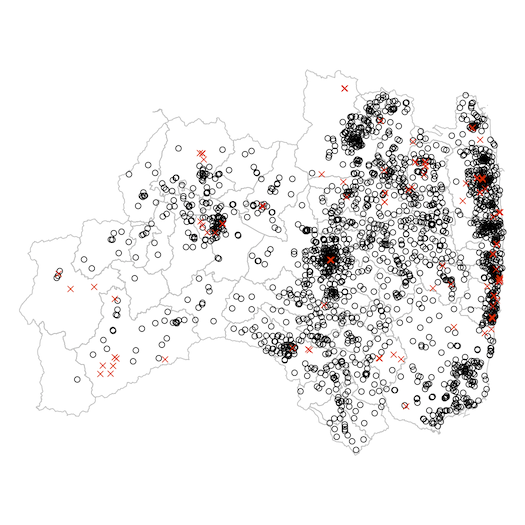
ちなみに,この期間に地上1mで線量率を測定しているリアルタイム線量測定システム(黒○)およびモニタリングポスト(赤×)の分布は次の通りである:
plot(st_geometry(fukushima), border="gray")
points(lon[!mp], lat[!mp])
points(lon[mp], lat[mp], pch=4, col="#ff2800")
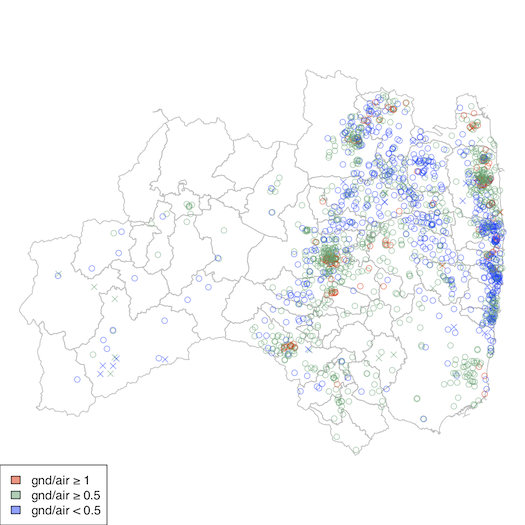
あまり見やすくないが,地上/航空の比で色分けすれば次のようになる(航空 < 0.1 は除いてある):
plot(st_geometry(fukushima), border="gray")
points(lon, lat, pch=ifelse(mp, 4, 1),
col=ifelse(rad/avi >= 1, "#ff280080", ifelse(rad/avi >= 0.5, "#35a16b80", "#0041ff80")))
par(family="Helvetica")
legend("bottomleft",
legend=c("gnd/air ≥ 1","gnd/air ≥ 0.5","gnd/air < 0.5"),
fill=c("#ff280080","#35a16b80","#0041ff80"), bg="white")
これはさすがに見にくいので,Leaflet と地理院地図で描きなおしたものをこちらに置いておく。
ちょうどこれを書いているときに 2019-01-20 の読売新聞朝刊に Naito ほか (2017) [4] の詳しい紹介が掲載された。そこで,Naito ほか [4] の Figure 1 に合わせて,第10次航空機モニタリング(2015年9月12日〜2015年11月4日)のデータで同じことをしてみる。データは放射性物質の分布状況等調査による航空機モニタリングの「福島県及びその近隣県における地表面から1m高さの空間線量率の測定結果(平成27年11月4日時点(事故から56か月後)) ( H27.11.4換算 )」のCSV(UTF-8)の「福島県」,および全国及び福島県の空間線量測定結果(日次平均値)の「全国及び福島県の空間線量測定結果(リアルタイム配信)日次平均値 ( H27.4~H28.3 )」のCSV(UTF-8)の「福島県」である。まずは飯舘村の線量分布を Naito ほか の Figure 1 とほぼ同じ色で描いてみよう:
mesh = read.csv("1010301013_07.csv", fileEncoding="UTF-8")
mesh[,8] = as.numeric(ifelse(grepl("<",mesh[,8]), "0", mesh[,8]))
iitate = subset(fukushima, N03_004=="飯舘村")
plot(st_geometry(iitate))
cols = function(x) {
ifelse(x < 0.2, "#c7b2de", ifelse(x < 0.5, "#b4ebfa", ifelse(x < 1, "#87e7b0",
ifelse(x < 1.9, "#cbf266", ifelse(x < 3.8, "#ffff99", "#edc58f")))))
}
rect(mesh[,15], mesh[,14], mesh[,11], mesh[,10], border=NA, col=cols(mesh[,8]))
plot(st_geometry(fukushima), add=TRUE)
par(family="Helvetica")
legend("bottomleft", bg="white",
legend=c("0.0μSv/h -","0.2μSv/h -","0.5μSv/h -","1.0μSv/h -","1.9μSv/h -","3.8μSv/h -"),
fill=c("#c7b2de","#b4ebfa","#87e7b0","#cbf266","#ffff99","#edc58f"))
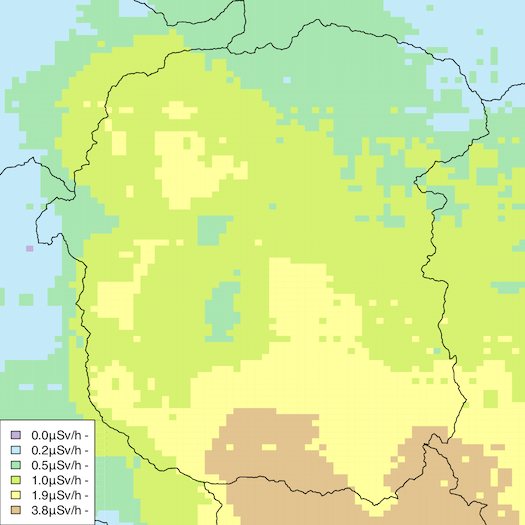
地上のデータとの比較:
files = dir(path="1010403005_07", pattern="*.csv", full.names=TRUE, recursive=TRUE)
n = length(files)
lat = lon = rad = avi = mp = rep(NA, n)
for (i in 1:n) {
a = read.csv(files[i], fileEncoding="UTF-8")
a = subset(a, 測定日 >= "2015-09-12" & 測定日 <= "2015-11-04")
if (dim(a)[1] == 0) next # 空であれば次に
lat[i] = mean(a[,5])
lon[i] = mean(a[,6])
rad[i] = mean(a[,8]) # 1ヶ月分の平均線量率
d = (lat[i] - mesh[,5])^2 + (lon[i] - mesh[,6])^2
k = which.min(d) # 最近接のメッシュ点を探す
avi[i] = mesh[k,8] # メッシュ点の航空機データ
d = (lat[i] - mplist[,8])^2 + (lon[i] - mplist[,7])^2
k = which.min(d) # 最近接のモニタリングポストを探す
mp[i] = (d[k] < 0.00001)
}
plot(avi[!mp], rad[!mp], log="xy", xlim=c(0.03,26), ylim=c(0.03,26), asp=1, xlab="航空機モニタリング", ylab="地上1m") # リアルタイム線量測定システム
points(avi[mp], rad[mp], pch=4, col="#ff2800") # モニタリングポスト
abline(0, 1)
curve(0.7*x, col="gray", add=TRUE)
curve(0.5*x, col="gray", add=TRUE)
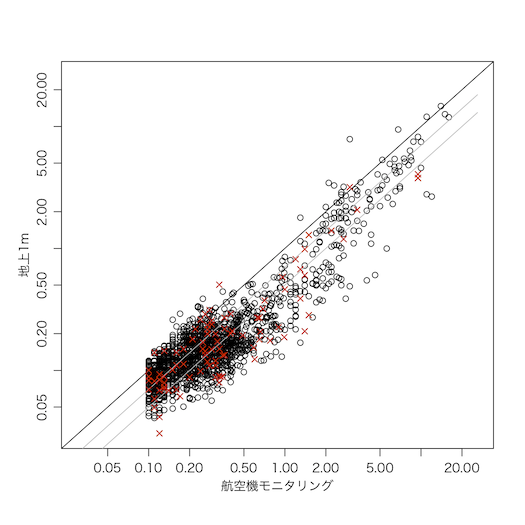
こちらの地上 / 航空機の比の中央値は 0.61 ほど(0.605998)である。
では,地上・航空機の両者が揃っている一番古いデータではどうか。放射性物質の分布状況等調査による航空機モニタリングの「第4次航空機モニタリングの空間線量率の測定結果 ( H23.11.5換算 )」の福島県と,全国及び福島県の空間線量測定結果(日次平均値)の最古の「全国及び福島県の空間線量測定結果(リアルタイム配信)日次平均値 ( H23.9~H24.3 )」を取得して,プロットしてみる。
options(stringsAsFactors=FALSE)
mplist = read.csv("mp-maker-memo.csv", header=FALSE, fileEncoding="UTF-8")
mesh = read.csv("1010301004_07.csv")
mesh[,8] = as.numeric(ifelse(grepl("<",mesh[,8]), "0", mesh[,8]))
files = dir(path="1010403001_07", pattern="*.csv", full.names=TRUE, recursive=TRUE)
n = length(files)
lat = lon = rad = avi = mp = rep(NA, n)
for (i in 1:n) {
a = read.csv(files[i], fileEncoding="UTF-8")
a = subset(a, 測定日 == "2011-11-05") # 2011年11月5日だけを選び出す
if (dim(a)[1] == 0) next # 空であれば次に
lat[i] = mean(a[,5])
lon[i] = mean(a[,6])
rad[i] = mean(a[,8]) # 1ヶ月分の平均線量率
d = (lat[i] - mesh[,5])^2 + (lon[i] - mesh[,6])^2
k = which.min(d) # 最近接のメッシュ点を探す
avi[i] = mesh[k,8] # メッシュ点の航空機データ
d = (lat[i] - mplist[,8])^2 + (lon[i] - mplist[,7])^2
k = which.min(d) # 最近接のモニタリングポストを探す
mp[i] = (d[k] < 0.00001)
}
plot(avi, rad, log="xy", xlim=c(0.067,20), ylim=c(0.067,20), asp=1,
xlab="航空機モニタリング", ylab="地上1m", pch=ifelse(mp, 4, 1))
abline(0, 1)
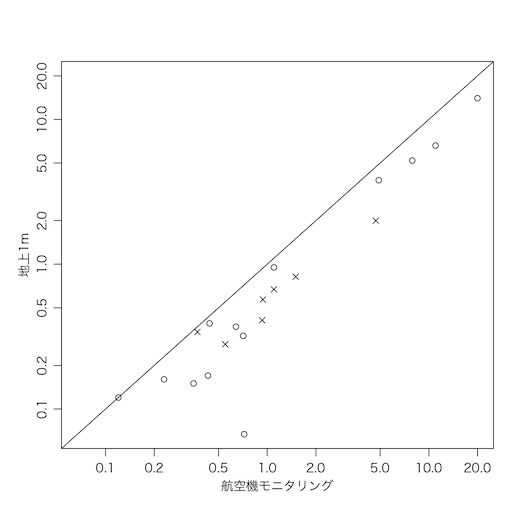
該当するデータが20点しかないが,地上/航空比はすべて1以下で,中央値は0.60(0.6031915)である。一番下の外れ値(地上/航空比 0.09305556)は,南会津郡南会津町「びわのかげ運動公園」(37.199049, 139.759041)[Googleマップで表示]である。ここは 2011-09-09 からデータが残っている:
x = read.csv("1010403001_07/1010403001_07_037199049_139759041.csv")
plot(as.Date(x[,1]), x[,8], type="o", pch=16, las=1, xaxt="n", xlab="", ylab="")
axis.Date(1, as.Date(x[,1]), format="%Y-%m-%d")
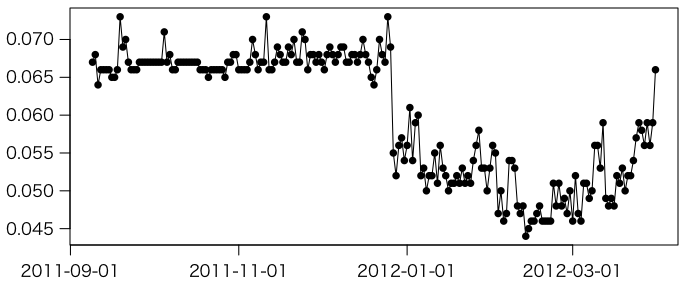
2011年12月27日に線量が急に減っている(除染?積雪?)。こういうグラフで具体的な日付を調べるには
identify(as.Date(x[,1]), x[,8], labels=as.Date(x[,1]))
と打ち込んでマウスで激減前後の点をクリックする。終了は右クリック(MacならCtrl+クリック)。終了時にコンソール出力されるのは連番である。
さらに,Miyazaki and Hayano [1] に合わせて,「第6次航空機モニタリング及び福島第一原子力発電所から80km圏外の航空機モニタリングの空間線量率の測定結果 ( H24.12.28換算 )」(放射性物質の分布状況等調査による航空機モニタリング)と「全国及び福島県の空間線量測定結果(リアルタイム配信)日次平均値 ( H24.4~H25.3 )」(全国及び福島県の空間線量測定結果(日次平均値))を伊達市に限定して調べてみよう:
mesh = read.csv("1010301008_07.csv", fileEncoding="UTF-8")
mesh[,8] = as.numeric(ifelse(grepl("<",mesh[,8]), "0", mesh[,8]))
mplist = read.csv("mp-maker-memo.csv", header=FALSE, fileEncoding="UTF-8")
files = dir(path="1010403002_07", pattern="*.csv", full.names=TRUE, recursive=TRUE)
n = length(files)
lat = lon = rad = avi = mp = rep(NA, n)
for (i in 1:n) {
a = read.csv(files[i], fileEncoding="UTF-8")
a = subset(a, 市町村 == "伊達市" & 測定日 >= "2012-12-01" & 測定日 <= "2012-12-31") # 伊達市の2012年12月分を抜き出す
if (dim(a)[1] == 0) next # 空であれば次に
lat[i] = mean(a[,5])
lon[i] = mean(a[,6])
rad[i] = mean(a[,8]) # 1ヶ月分の平均線量率
d = (lat[i] - mesh[,5])^2 + (lon[i] - mesh[,6])^2
k = which.min(d) # 最近接のメッシュ点を探す
avi[i] = mesh[k,8] # メッシュ点の航空機データ
d = (lat[i] - mplist[,8])^2 + (lon[i] - mplist[,7])^2
k = which.min(d) # 最近接のモニタリングポストを探す
mp[i] = (d[k] < 0.00001)
}
plot(avi, rad, log="xy", xlim=c(0.11,1.5), ylim=c(0.11,1.5), asp=1,
xlab="航空機モニタリング", ylab="地上1m", pch=ifelse(mp, 4, 1))
abline(0, 1)

地上/航空機の中央値 median(rad/avi, na.rm=TRUE) は 0.6128889 である。
中央値の統計誤差をブートストラップで求めてみよう:
ratio = (rad/avi)[!is.na(rad/avi)] # または ratio = na.omit(rad/avi)
r = replicate(100000, median(sample(ratio, replace=TRUE)))
sd(r) # だいたい 0.054 くらい
つまり,この中央値とその統計誤差(標準誤差)は 0.61 ± 0.05 と書ける。