カイ2乗検定

ポアソン分布からカイ2乗分布へ

個数 $n_1$, $n_2$, $n_3$, $\ldots$ が独立で，それぞれ平均 $\mu_1$, $\mu_2$, $\mu_3$, $\ldots$ のポアソン分布をするとします。ポアソン分布ですから $n_i$ の分散はその平均 $\mu_i$ に等しく，$n_i$ が10程度以上であれば正規分布で近似できるので，個数から平均を引いて標準偏差で割ればほぼ標準正規分布 $N(0,1)$ に従います。すると，

\[ \chi^2 = \sum_{i=1}^N \frac{(n_i - \mu_i)^2}{\mu_i} \]

は独立な標準正規分布の2乗の $N$ 個の和です。一般に，独立な標準正規分布の2乗の $N$ 個の和の確率分布を，自由度 $N$ のカイ2乗分布と呼びます。

具体的な問題を考えましょう。毎年の事故発生件数が $n_1$, $n_2$, $n_3$, $\ldots$, $n_N$ であるとき，1年あたりの平均事故件数は

\[ m = \frac{1}{N} \sum_{i=1}^N n_i \]

になります。したがって，これらが独立にポアソン分布に従うという帰無仮説のもとで

\[ \chi^2 = \sum_{i=1}^N \frac{(n_i - m)^2}{m} \]

は自由度 $N$ のカイ2乗分布に従いそうですが，ここでは $m$ は実際のデータから計算していますので，正しくは自由度 $N-1$ のカイ2乗分布になります。

個数の列が与えられたとき，上の $\chi^2$ の値を計算し，それがカイ2乗分布で予想される範囲から外れていれば，独立なポアソン分布であるという帰無仮説が疑わしくなります。このことを使った検定法は，ピアソン（Karl Pearson）のカイ2乗検定（$\chi^2$ 検定）と呼ばれます。

例えばPISA「盗難事件」問題ほかで挙げた6年間の事故発生件数

> x = c(762,792,795,794,849,834)

が独立なポアソン分布に従うという帰無仮説についてカイ2乗検定をしてみましょう。Rでは次のようにして簡単に計算できます。

> chisq.test(x)

	Chi-squared test for given probabilities

data:  x 
X-squared = 6.2329, df = 5, p-value = 0.2842

$p$ 値は 0.2842 ですので，帰無仮説と矛盾しません。

分割表のカイ2乗検定

2×2分割表の縦計・横計

\[ \begin{array}{cc|c} a & b & e \\ c & d & f \\ \hline g & h & n \end{array} \]

が与えられたとき，もし表の各行（各列）が独立ならば，

\[ \begin{array}{cc|c} \frac{eg}{n} & \frac{eh}{n} & e \\ \frac{fg}{n} & \frac{fh}{n} & f \\ \hline g & h & n \end{array} \]

になるはずです。この予測値（期待度数）と実際の値（観測度数）との差の2乗を予測値で割ったものの合計

\[ \frac{(a - eg/n)^2}{eg/n} + \frac{(b - eh/n)^2}{eh/n} + \frac{(c - fg/n)^2}{fg/n} + \frac{(d - fh/n)^2}{fh/n} \]

は近似的に自由度1の $\chi^2$（カイ2乗）分布に従います。自由度が1であることは，縦横の合計を固定した $2 \times 2$ 分割表の自由度が一つしかないことを考えれば納得できるでしょう。$n_1 \times n_2$ 分割表では自由度は $(n_1-1)(n_2-1)$ になります。

$2 \times 2$ 分割表の場合に限って，それぞれの「予測値と実際の値との差」を0に近い側に0.5ずつ修正するというイェーツの連続性の補正（Yates' continuity correction）をする場合があります。

Rで $\chi^2$ 検定をする関数は chisq.test() です。単に

> chisq.test(matrix(c(228,863,284,851),nrow=2))

などとすれば，$2 \times 2$ 分割表の場合に連続性の補正を行います。結果は $p = 0.02377$ です。連続性の補正を行いたくないなら，

> chisq.test(matrix(c(228,863,284,851),nrow=2), correct=FALSE)

のようにします。結果は $p = 0.02082$ となります。ちなみに Fisherの正確検定 の結果は $p = 0.02335$ です。

「カイ2乗…」と書いても「カイじじょう…」と読む人が多いのは，昔「2乗」のことを「自乗」（じじょう）と言ったことの名残りだろうと思います（私は「にじょう」と読みます）。

$p$ 値は，連続性の補正をすれば大きめになり，しなければ小さめになります。 Fisherの正確検定かカイ2乗検定か も参考にしてください。

［この項要再検討］ 観測度数を $O_i$，期待度数を $E_i$ とすると，$\chi^2$ 検定は

\[ \chi^2 = \sum_i (O_i - E_i)^2 \big/ E_i \]

を使いますが，類似のものとして，G検定（G-test）があります。これは

\[ G = 2 \sum_i O_i \cdot \log (O_i / E_i) \]

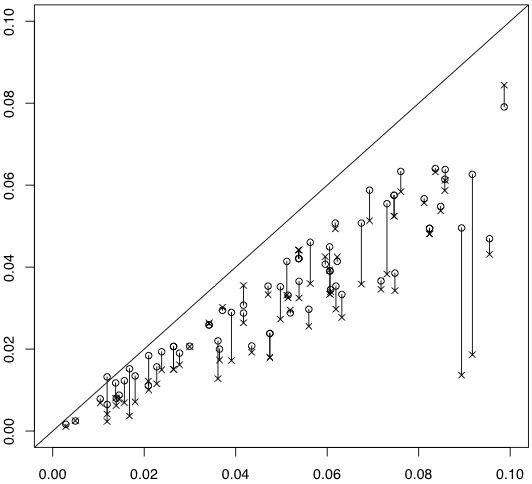
の分布が同じ $\chi^2$ 分布で近似できることを使います（$O_i = 0$ の項は対数が計算できませんが，単に 0 として計算します）。分野によっては $\chi^2$ 検定より人気があるようです。図は各セルに入る確率が $\bigl[\begin{smallmatrix} 0.12 & 0.28 \\ 0.18 & 0.42 \end{smallmatrix} \bigr]$ で与えられる総度数50の $2 \times 2$ 分割表を1000個作って，横軸はFisherの方法の $p$ 値，縦軸は連続性の補正なしの $\chi^2$ 検定の $p$ 値（○）とG検定の $p$ 値（×）をプロットし，対応する○と×を線分で結んだものです。

少なくともこの場合にはG検定の $p$ 値は小さすぎることがわかります。

このシミュレーションに使ったプログラムは次の通りです：

prob = c(0.12,0.18,0.28,0.42)
ni = 1000
pfis = pchi = pg = numeric(ni)
for (i in 1:ni) {
  k = sample(1:4, 50, replace=TRUE, prob=prob)
  na = sum(k == 1)
  nb = sum(k == 2)
  nc = sum(k == 3)
  nd = sum(k == 4)
  a = matrix(c(na, nb, nc, nd), nrow=2)
  pfis[i] = fisher.test(a)$p.value
  pchi[i] = chisq.test(a, correct=FALSE)$p.value
  pg[i]   = g.test(a)$p.value
}
plot(pfis, pchi, xlim=c(0,0.1), ylim=c(0,0.1), xlab="", ylab="")
abline(0,1)
for (i in 1:ni) {
  if (!is.na(pchi[i])) {
    points(pfis[i], pg[i], pch=4)
    lines(c(pfis[i],pfis[i]), c(pchi[i],pg[i]))
  }
}

度数分布データと仮説との整合性を調べる $\chi^2$ 検定では，$\chi^2 (\geq 0)$ の値が大きいほど仮説からの外れが大きいので，通常は大きい側だけを調べればいいのですが，逆に 0 に近すぎる（仮説と合いすぎる）場合も，データ改竄が疑われるという意味で，興味があります。例えば有名な遺伝の法則を発見したメンデルのデータは，理論値 $3:1$ に合いすぎているという指摘がされています（R. A. Fisher, ``Has Mendel's work been rediscovered?'', Annals of Science 1, 115-137 (1936); C. R. ラオ『統計学とは何か―偶然を生かす』（藤越康祝ほか訳，丸善，1993年））。

Last modified: