Fisherの正確検定かカイ2乗検定か

[2017-09-19] 黒木玄さんが追試をしてくださって，このページの ECDF for chisq.test(correct=T) の図が微妙に違うと教えていただきました。図のタイムスタンプは 2009-01-25 ですが，chisq.test() の仕様が変わったとも考えられず，おそらく私のミスだと思われますじゃなく本当に仕様変更でした。それを除いても，図の見栄えが今のRの出力と微妙に違います。そもそもHTMLも5になってなかったし，数式もMathJaxでなかったので，全面的に書き直しました。

[2017-09-20] 黒木玄さんが解決してくださいました。本当にRの chisq.test() の仕様が変わったのでした（ここ参照）。黒木さんはほかにもいろいろ貴重なことを書いてくださっていますのでこのツイートの前後の連鎖をご覧ください（私もまだ消化しきれていません）。

[2017-10-31] r-statistics-fanさんのFisher's exact testが"正確”かどうかも参考になります。

例

次のような2×2分割表を考えましょう。

$a$$b$20
$c$$d$30
153550

このような表の各行・各列が独立かどうかを検定する際の帰無仮説として，次の二つを考えます：

以下では，上の場合を条件なし（unconditional），下の場合を条件付き（conditional）と呼んでいます。これ以外に，右の周辺度数（20，30）だけ固定し，下の周辺度数は固定しないなども考えられます。

このような分割表の検定としては，Fisherの正確検定とカイ2乗検定がよく使われています。前者は条件付きの場合に正確な $p$ 値を与える方法です。

これらの場合について，それぞれ $n$ 回シミュレーションし，

\[ F_n(x) = \text{($p$ 値が $x$ 以下の回数)} / n \]

を求めてみましょう。この $F_n(x)$ を経験分布関数または経験累積分布関数（ECDF，empirical cumulative distribution function）といいます。

グラフは次のようになります。横軸は $x$，縦軸は $F_n(x)$ です。

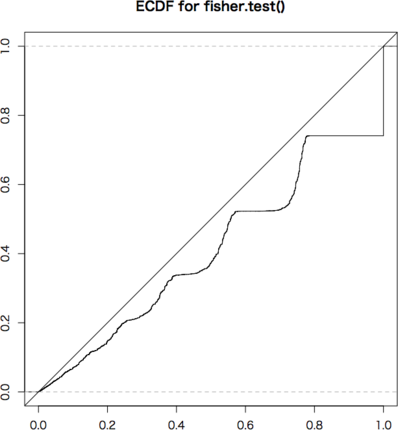
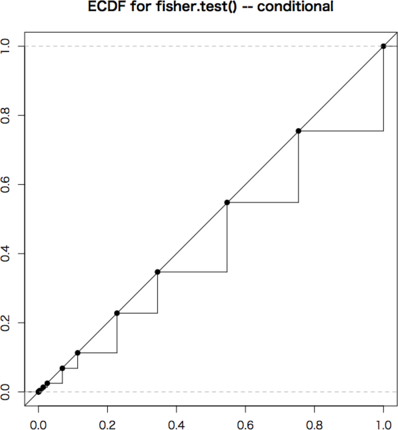
ECDF for fisher.test() ECDF for fisher.test() -- conditional
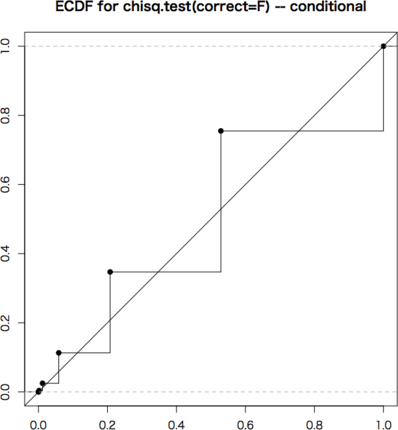
ECDF for chisq.test(correct=F) ECDF for chisq.test(correct=F) -- conditional
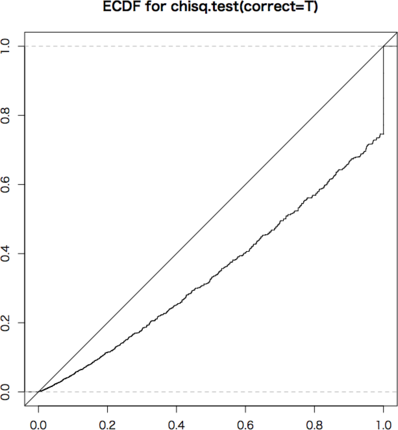
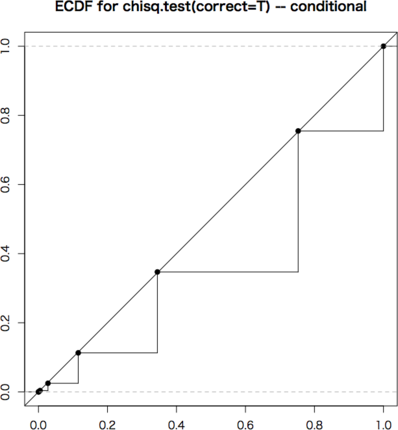
ECDF for chisq.test(correct=T) ECDF for chisq.test(correct=T) -- conditional

ECDFは，斜め45度の線上にあるのが理想です。条件付きの2×2分割表は非常に離散的で，いくつかの $p$ 値しかとりません。グラフではぎざぎざになっていますが，可能な場合（黒丸の点）については完全に斜め45度の線上にありますので，条件付きの場合はFisherの方法が最適です。これを近似するものとして連続性の補正をしたカイ2乗検定があります。

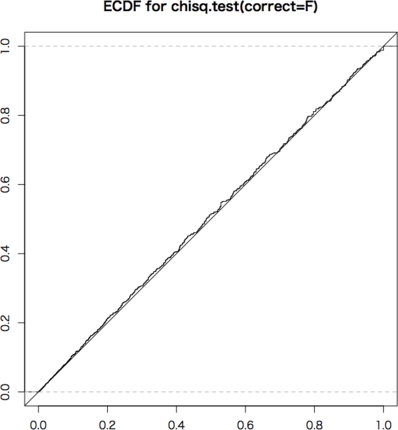
問題は条件なしの場合で，Fisherの方法は，下に寄ってしまいます。$p \leq 0.05$ となる確率は 0.03〜0.04 程度です。全体の形としては，補正なしのカイ2乗検定が最も良くなります。

これは条件付き・条件なしの本質的な違いではなく，単に条件付きの場合は可能な点が少ないのでより離散的になるためです。サンプルのサイズ（この例では50）をもっと増やせば違いはなくなります。

練習問題として，片側だけ条件付きの場合もやってみてください（条件なしの場合とほぼ同じ図になります）。

Rのプログラム

条件なしの場合：

prob = c(0.12,0.18,0.28,0.42)
ni = 100000
pfis = pchi = pchic = numeric(ni)
for (i in 1:ni) {
  k = sample(1:4, 50, replace=TRUE, prob=prob)
  na = sum(k == 1)
  nb = sum(k == 2)
  nc = sum(k == 3)
  nd = sum(k == 4)
  a = matrix(c(na, nb, nc, nd), nrow=2)
  pfis[i] = fisher.test(a)$p.value
  pchi[i] = chisq.test(a, correct=FALSE)$p.value
  pchic[i] = chisq.test(a, correct=TRUE)$p.value
}

plot(ecdf(pfis), asp=1, xlab="", ylab="", xlim=c(0,1), ylim=c(0,1),
     verticals=TRUE, main="ECDF for fisher.test()")
abline(0,1)

条件付きの場合は上の k = ... を次のようにします：

  k = sample(c(rep(1,15),rep(3,35))) + sample(c(rep(0,20),rep(1,30)))

追記：Barnardの正確検定

ExactパッケージにBarnard/Boschlooの正確検定が収められている（Which test for cross table analysis: Boschloo or Barnard? も参照）。これらは，行・列のマージンを固定するFisherの正確検定と違って，行マージンだけ固定するモデル（"Binomial"，デフォルト）および全カウントのみ固定するモデル（"Multinomial"）が可能である。

library(Exact)

行の比率を 20:30 に固定して，列だけ 0.3, 0.7 の2項分布にする：

  k = sample(c(1,3), 50, replace=TRUE, prob=c(0.3,0.7)) +
      sample(c(rep(0,20),rep(1,30))) # row binom

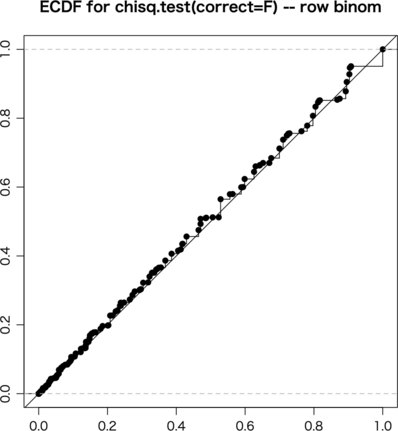
これで fisher.test(a)，chisq.test(a, correct=FALSE)，chisq.test(a, correct=TRUE)，exact.test(a, to.plot=FALSE)，exact.test(a, cond.row=FALSE, to.plot=FALSE) をそれぞれ試してみる。ただし exact.test() は遅いので ni = 10000 とした：

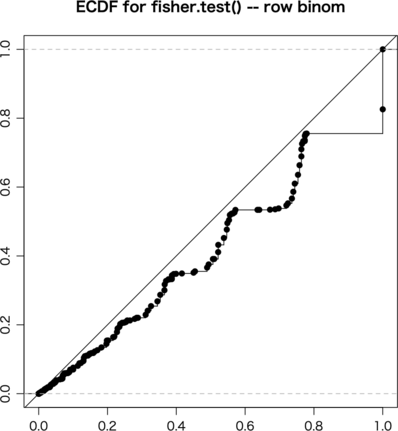
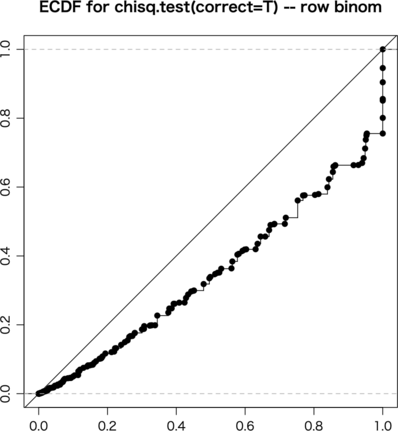
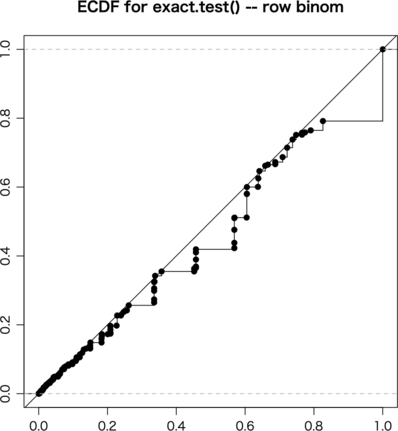
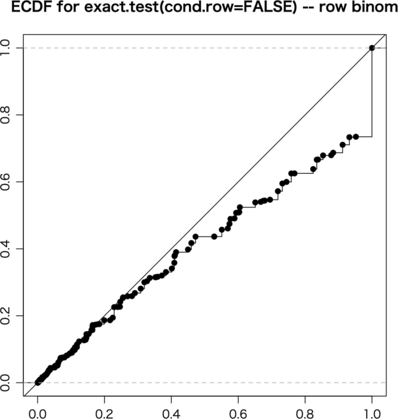
ECDF for fisher.test() -- row binom ECDF for chisq.test(correct=F) -- row binom ECDF for chisq.test(correct=T) -- row binom ECDF for exact.test() -- row binom ECDF for exact.test(cond.row=F) -- row binom

行ごとに固定したので exact.test(a, cond.row=FALSE, to.plot=FALSE) はうまくいかなくても当然である。

最後に k = sample(1:4, 50, replace=TRUE, prob=prob) で行も列も固定せず全体の数だけ固定する exact.test(a, model="Multinomial") を試してみる。非常に遅いので ni = 1000 とした：

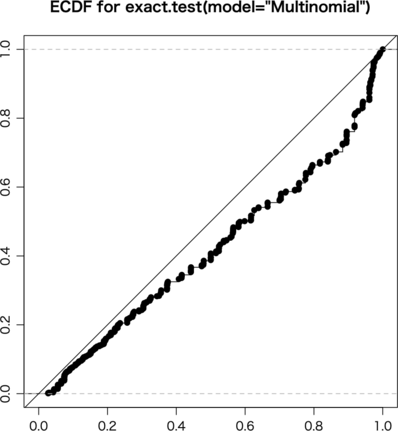
ECDF for exact.test(model='Multinomial')

まとめると，周辺分布固定という fisher.test() の仮定が満たされる場合以外は，chisq.test(correct=FALSE) が平均的には良さそうである。ただ，検定は strict でなければならない（辛い分にはよい）という考え方もあって，そういう向きには正確検定が好まれそうである。