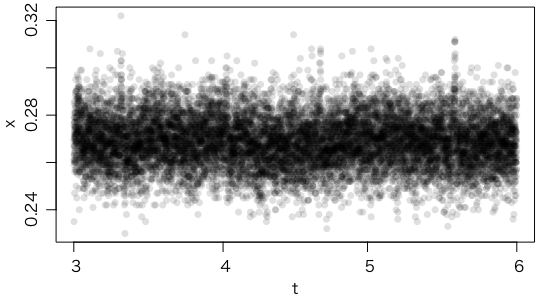
郡山駅東口の線量計(正式な名称は「リアルタイム線量測定システム」,写真)を見ていると,ゆらぎがけっこうある。原子力規制委員会の放射線モニタリング情報からCSVデータをダウンロードして調べてみた。冬は積雪時に遮蔽効果で線量が低くなるので,2015年3月〜5月の3ヶ月間のデータを調べる。
放射線モニタリング情報のサイトからダウンロードしたファイルは db.csv というファイル名である。このCSVファイルをRの read.csv() で読む際には,ヘッダ(1行目の項目名)がないので header=FALSE を指定する。文字コードはシフトJIS(をMicrosoftが拡張したCP932)なので fileEncoding="CP932" も指定する:
d = read.csv("db.csv", header=FALSE, fileEncoding="CP932")
t = as.POSIXct(d[,5]) # 5列目が年月日(POSIXct型)
n = length(t) # データ点数
x = d[,6] # 6列目が線量率(μSv/h)
こういう時系列は,通常は
plot(t, x, type="l")
のようにして折れ線グラフにするのだが,データ点数が多いのと,ホワイトノイズが乗っているので,真っ黒になってしまう。そこで,黒丸(pch=16)にアルファチャンネルを付けて少し透明にしてみる(col="#00000020")。この最後の 20 という透明度(16進2桁)を加減すれば,黒さを調節できる:
plot(t, x, pch=16, col="#00000020")

ほぼランダムなように見える。日周変化(次のようにしてプロットできる)は,なさそうだ。日周変化を調べる次のベタな方法は,日時を内部表現の数値(UNIX時刻,1970年からの秒数,UTC)as.numeric(t) に直して,9時間(3600*9)を加えてJSTにし,24時間(3600*24)で割った剰余(%%)を求めて,それをさらに3600で割って時間に直す:
plot(((as.numeric(t) + 3600*9) %% (3600*24)) / 3600, x, pch=16, col="#00000020")
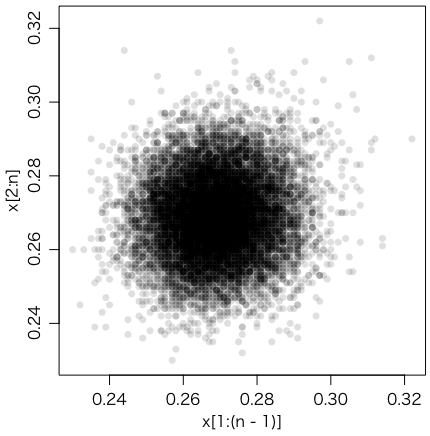
隣同士の相関もほとんどない(asp はアスペクト比)。
plot(x[1:(n-1)], x[2:n], pch=16, col="#00000020", asp=1)
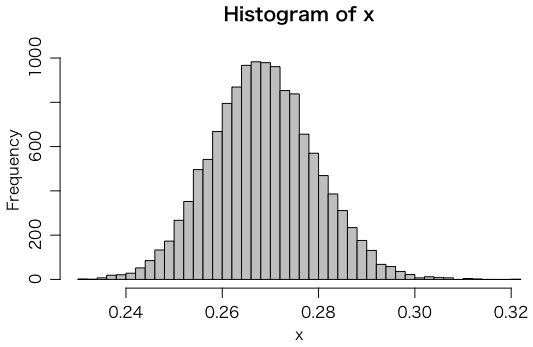
ヒストグラムも描いてみよう。実はこのデータは X.XXX μSv/h のように小数第3位まで公開されているのだが,最下位桁はほぼノイズなので小数第2位までで十分だという議論がある。しかし,分布を調べるには小数第3位まであったほうがよい:
hist(x, col="gray", breaks=50)
10分ごとに計測されたこの分布を,ポアソン分布に従う計数値に比例するとしよう。平均 mean(x) は 0.2690509,標準偏差 sd(x) は 0.01084415,両者の比の2乗 (mean(x) / sd(x))^2 は 615.5699 であり,この値が計数値の平均になる。1分あたりだと 61.55699 で,これが 0.2690509μSv/h に相当するので,割り算すると 228.7931,つまり約 230 cpm/(μSv/h) ということになる。標準偏差の2乗は分散 var() なので,まとめると,
mean(x) / var(x) / 10
で cpm/(μSv/h) 値が求められる。最後の 10 は1データ点あたりの計測時間(分)である。
ちなみに,後述の「思い付いた方法」を使ってみると,
x1 = x[1:(n-1)]
x2 = x[2:n]
1 / mean((x1-x2)^2 / (x1+x2)) / 10
244.8525 となり,上の値より7%ほど大きい。
こちらは固定型(いわゆるモニタリングポスト)で,やはり2015年3〜5月である。ホワイトノイズではなく信号が見えるようなので,通常の折れ線グラフでプロット:
plot(t, x, type="l")
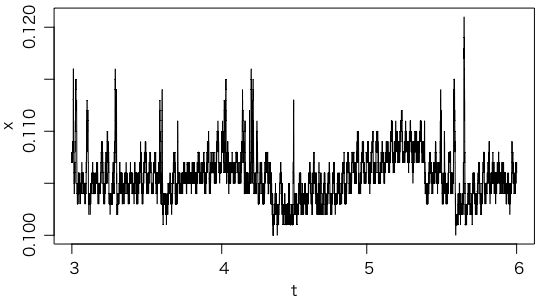
9点の移動平均をとって,重ね書きしてみる:
y = filter(x, rep(1/9,9))
points(t, y, type="l", col="red")
ちょっとわかりにくいので,残差をプロットしてみる:
d = x - y
plot(t, d, pch=16, col="#00000020")
ヒストグラム:
hist(d, col="gray", breaks=50)
残差の隣同士の相関:
plot(d[1:(n-1)], d[2:n], pch=16, col="#00000020", asp=1)
このように,測定値の量子化誤差によるアーティファクトがあらわになってしまう。とりあえずそれは無視して機械的にセンサ感度を調べてみる(10は1データ点あたり10分間測定):
mean(x) / var(d, na.rm=TRUE) / 10
約 35000 cpm/(μSv/h) であることがわかる。
より単純にトレンドを除去するために差分をとってみる:
d = diff(x) # 次に同じ: d = x[2:n] - x[1:(n-1)]
2 * mean(x) / var(d) / 10 # 差分の分散は元の分散の2倍
これだとおおよそ 33000 cpm/(μSv/h) 程度になる。
日周変化を見るには,1日(144点)より長い移動平均との差を,毎日の時刻を横軸にとってプロットすればよい:
y = filter(x, rep(1/401,401))
d = x - y
plot(((as.numeric(t) + 3600*9) %% (3600*24)) / 3600, d, pch=16, col="#00000010")
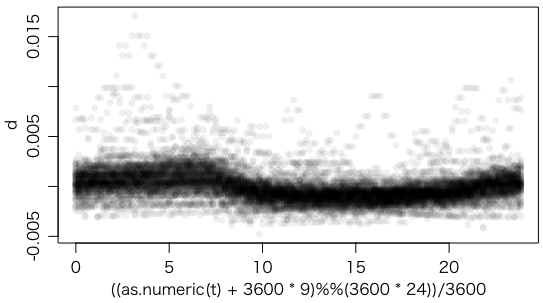
人の活動時間は線量が減っているように見える。
cpm/(μSv/h)値は mean(x) / var(x) / 分 で求められるが,x1 = x[1:(n-1)],x2 = x[2:n] と置くと,var(x) は mean((x1-x2)^2) / 2 とほぼ等しい。したがって,var(x) / mean(x) は mean((x1-x2)^2 / (x1+x2)) とほぼ等しい。
x1 = x[1:(n-1)]
x2 = x[2:n]
1 / mean((x1-x2)^2 / (x1+x2)) / 10
とすると,33000 cpm/(μSv/h) 程度になる。このほうが,x のトレンドに強い。
もし線量計が10分ごとのカウント値をそのまま使うのでなく,前の10分のカウント値も併用していて,隣接する値に相関がある場合は,相関が消えるだけ間隔を付けてみるといいかもしれない:
x1 = x[1:(n-2)]
x2 = x[3:n]
1 / mean((x1-x2)^2 / (x1+x2)) / 10
ただ,間隔が増えるにつれて,今度はトレンドの影響が出るので,感度が低めに出てしまう。
この方法と,9点の移動平均を引いてから分散を求める方法を,比較してみた。正解は100cpm/(μSv/h)であるが,次第に変化の速い変動を付けている。
foo = function(k) {
n = 1000
x = rpois(n, 200+100*sin(2*pi*k*(0:(n-1))/n)) / 1000
x1 = x[1:(n-1)]
x2 = x[2:n]
d = x - filter(x, rep(1/9,9))
c(1 / mean((x1-x2)^2/(x1+x2)) / 10, mean(x) / var(d,na.rm=TRUE) / 10)
}
a = sapply((0:500)/10, foo)
plot((0:500)/10, a[1,], ylim=range(a[1,],a[2,]), xlab="k", ylab="cpm/(μSv/h)")
points((0:500)/10, a[2,], col="red")
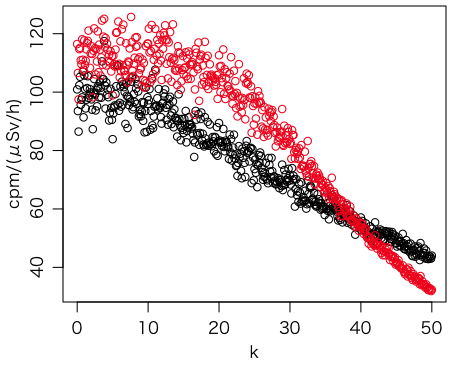
提案の方法(黒)のほうが良い。移動平均を引く方法(赤)では,変化が少ないところでは過大評価になり,変化が増えると急速に過小評価になることがわかる。
なお,提案の方法で mean() を median() や mean(trim=0.1) などにするのはよくないが,大きい値を除いて平均するのは意味があるかもしれない。
jsdfq43wtrさんが現場を回ってメーカーを調べてくださった(mp-maker-memo.csv)。これを読んで例えばN社のデータだけを1日分JSONで取ってくるスクリプトを作るにはRubyで次のようにすればよい(RでJSONを読む参照):
require "csv"
CSV.foreach("mp-maker-memo.csv") do |row|
if row[9] == "N"
puts "wget http://radioactivity.nsr.go.jp/data/ja/real/area_#{row[1]}/#{row[2]}_trend.json"
end
end
同様にしてF社も取得し,それぞれ N,F というサブディレクトリに収める。よく見るとF社のものにはMで始まる可搬型モニタリングポストも混じっている(jsdfq43wtrさんのモニタリングポストの種別参照)。試行錯誤の末,次のようにして,横軸を平均線量,縦軸を感度として,メーカーごとにプロットした。
N = dir("N", "^1.*\\.json$", full.names=TRUE)
F = dir("F", "^1.*\\.json$", full.names=TRUE)
M = dir("F", "^M.*\\.json$", full.names=TRUE)
foo = function(f) {
x = fromJSON(f)
v = x$day$air$value # これでair/airF/airMのどれかを拾う
v = ifelse(v == 0, NA, v) # 0は欠損値
n = length(v)
v1 = v[1:(n-1)]
v2 = v[2:n]
c(mean(v, na.rm=TRUE), 1 / mean((v1-v2)^2/(v1+v2), na.rm=TRUE) / 10)
}
cN = sapply(N, foo)
cF = sapply(F, foo)
cM = sapply(M, foo)
plot(NULL, xlim=range(c(cN[1,],cF[1,],cM[1,])), ylim=range(c(cN[2,],cF[2,],cM[2,])),
xlab="μSv/h", ylab="cpm/(μSv/h)", log="xy")
points(cN[1,], cN[2,], pch="N", col="blue")
points(cF[1,], cF[2,], pch="F", col="black")
points(cM[1,], cM[2,], pch="M", col="red")
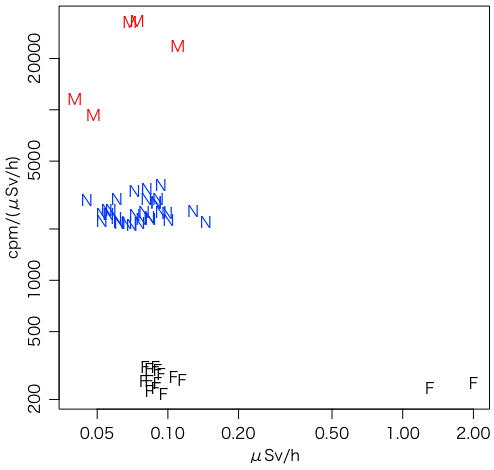
感度は,モニタリングポストは10000〜30000,N社は2000〜3000,F社は200〜300であることがわかる。
F社で一番線量が高いところにあるものがNo.102200(飯舘村/福島県立相馬農業高等学校飯舘校)である。この2015-03-01 00:00から2015-06-28 00:00までのデータをCSVで取得して解析してみた:
plot(t, x, pch=16, col="#00000020") # かなりトレンドがある
cor(x[1:(n-1)], x[2:n]) # 0.7680932 強い正の相関
mean(x) / var(x) / 10 # 56.87193 これは小さすぎる
y = filter(x, rep(1/9,9)) # 9点で平滑化
d = x - y
cor(d[1:(n-1)], d[2:n], use="complete.obs") # -0.1346533 かなり負
mean(x) / var(d, na.rm=TRUE) / 10 # 274.4076 少し大きすぎ
y = filter(x, rep(1/25,25)) # ±2時間の平滑化
d = x - y
cor(d[1:(n-1)], d[2:n], use="complete.obs") # -0.02275492 ほぼ無相関
plot(d[1:(n-1)], d[2:n], pch=16, col="#00000020", asp=1) # ほぼ円
mean(x) / var(d, na.rm=TRUE) / 10 # 250.5785
x1 = x[1:(n-1)]
x2 = x[2:n]
1 / mean((x1-x2)^2 / (x1+x2)) / 10 # 245.0939
245 cpm/(μSv/h) 程度の感度である。
一方,N社で一番線量が高いところにあるのがNo.102278(会津若松市/会津若松市大木の芝原公園)である。こちらは3月に大きな変動があり,4月以降落ち着くので,2015-04-01 00:00から2015-06-28 00:00までを調べてみる:
plot(t, x, pch=16, col="#00000020") # まだトレンドがある
cor(x[1:(n-1)], x[2:n]) # 0.7684599 強い正の相関
mean(x) / var(x) / 10 # 601.4008 これは小さすぎる
y = filter(x, rep(1/9,9)) # 9点で平滑化
d = x - y
cor(d[1:(n-1)], d[2:n], use="complete.obs") # -0.1150526 かなり負
mean(x) / var(d, na.rm=TRUE) / 10 # 2888.883 少し大きすぎ
y = filter(x, rep(1/15,15))
d = x - y
cor(d[1:(n-1)], d[2:n], use="complete.obs") # -0.01281046 ほぼ無相関
plot(d[1:(n-1)], d[2:n], pch=16, col="#00000020", asp=1) # ほぼ円
mean(x) / var(d, na.rm=TRUE) / 10 # 2625.594
x1 = x[1:(n-1)]
x2 = x[2:n]
1 / mean((x1-x2)^2 / (x1+x2)) / 10 # 2599.197
2600 cpm/(μSv/h) 程度の感度である。
このようにN社製のほうが感度が1桁高いので,比較的低線量の地点に配置するのは理にかなっている。これだけの精度が本当に必要かどうかは別の話である。
オマケ:例えばこのNo.102278のデータをコマンドで取得するには次のようにする:
wget --post-data='ParentArea=07G&AreaCode=07202&StationCode=102278&DataType=real&SensorCode=air&StartDate=2015-04-01&StartHour=00&StartMinute=00&EndDate=2015-06-28&EndHour=00&EndMinute=00&IntervalMinute=10' http://radioactivity.nsr.go.jp/monitor_sv/downloadCSV
RでJSONを読むにある方法で福島県の全部のJSONファイルを取得し,上の方法を適用してみた。分類はファイル名のパターン(以下の正規表現参照)で行った。JSONファイルの10分ごとデータは1日分(144点)しかないので,誤差がかなりある。
files4 = dir(pattern="^[0-9]{4}_trend\\.json$")
files6 = dir(pattern="^[0-9]{6}_trend\\.json$")
files10 = dir(pattern="^[0-9]{10}_trend\\.json$")
filesHG = dir(pattern="^HG[0-9]*_trend\\.json$")
filesM = dir(pattern="^M[0-9]*_trend\\.json$")
c4 = sapply(files4, foo)
c6 = sapply(files6, foo)
c10 = sapply(files10, foo)
cHG = sapply(filesHG, foo)
cM = sapply(filesM, foo)
plot(NULL,
xlim=range(c(c4[1,],c6[1,],c10[1,],cHG[1,],cM[1,]),na.rm=TRUE),
ylim=range(c(c4[2,],c6[2,],c10[2,],cHG[2,],cM[2,]),na.rm=TRUE),
xlab="μSv/h", ylab="cpm/(μSv/h)", log="xy", type="n")
points(c6[1,], c6[2,], pch="6", col="#663300")
points(cM[1,], cM[2,], pch="M", col="#ff9900")
points(cHG[1,], cHG[2,], pch="H", col="#35a16b")
points(c10[1,], c10[2,], pch="0", col="#ff2800")
points(c4[1,], c4[2,], pch="4", col="#0041ff")
当初の図の後,範囲を全国に広げ,2週間分のデータを使って描きなおしたものが次の図である:
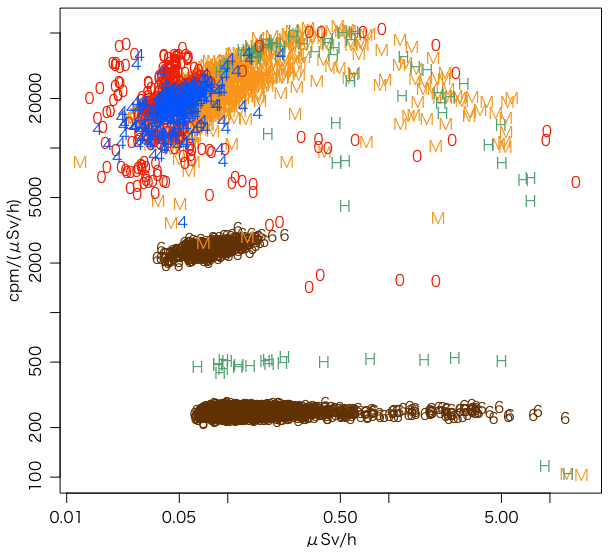
ちなみに,上のプログラムをちょっと変えて,横軸に最大値と最小値の差,縦軸に比をとってグラフを描いてみる:
foo = function(f) {
x = fromJSON(f)
v = x$day$air$value
v = ifelse(v == 0, NA, v)
c(max(v,na.rm=TRUE) - min(v,na.rm=TRUE),
max(v,na.rm=TRUE) / min(v,na.rm=TRUE))
}
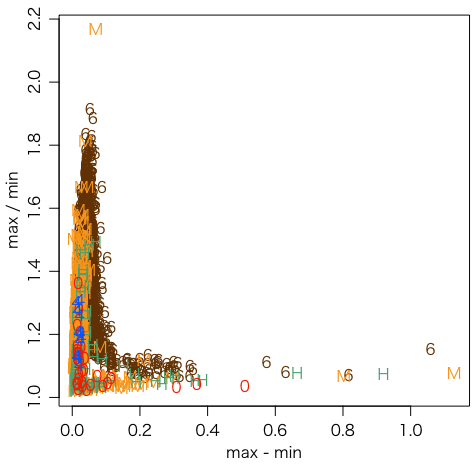
この図から,例えば差が0.2μSv/hかつ比が1.2以上といった異常値検出の方法が使えるかもしれないことが考えられる。
東京都の環境放射線測定結果のデータは1時間きざみであるが,原子力規制委員会サイトには10分きざみの値が掲載されている(ただし2012/03/30 00:10以降)。1日(144点,オレンジ),1週間(1008点,緑),1ヶ月(4320点,青)の3通りの窓を使い,横軸に窓の位置,縦軸に計算結果(感度)をプロットした。左側ほど新しい時間である。
d = read.csv("db.csv", header=FALSE, fileEncoding="CP932")
x = d[,6]
n = length(x)
bar = function(s, w) {
x1 = x[s:(s+w-1)]
x2 = x[(s+1):(s+w)]
1 / mean((x1-x2)^2 / (x1+x2)) / 10
}
plot(1:(n-144), sapply(1:(n-144), bar, 144), pch=16, type="l", col="#ff9900",
xlab="", ylab="cpm/(μSv/h)", panel.first=grid())
points(1:(n-1008), sapply(1:(n-1008), bar, 1008), pch=16, type="l", col="#35a16b")
points(1:(n-4320), sapply(1:(n-4320), bar, 4320), pch=16, type="l", col="#0041ff")
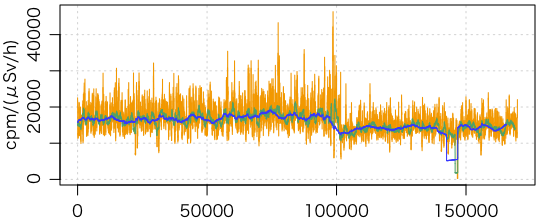
おそらく16000cpm/(μSv/h)程度と思われる。1日の集計では誤差が大きいこともこの図からわかる。
飯舘村がモニタリングポスト88基運用開始(福島民報,2016/03/17)。
というわけで,飯舘村 放射線量マップができた。データはCSVでダウンロードできる。2016-03-16 00:00までの全データをダウンロードしてここに置いておいた。
感度の分布を見てみよう:
rad = read.csv("http://okumuralab.org/~okumura/stat/data/iitate20160316.csv",
fileEncoding="CP932", as.is=TRUE)
id = unique(sort(rad$機器ID))
f = function(i, plot=FALSE) {
r = subset(rad, 機器ID==i)
x = r$測定値1m
if (plot) {
t = as.POSIXct(paste(r$測定日, r$測定時刻, sep=" "))
plot(t, x, type="l")
}
n = length(x)
x1 = x[1:(n-2)]
x2 = x[3:n]
1 / mean((x1-x2)^2 / (x1+x2)) / 10
}
s = sapply(id, f)
hist(log10(s), col="gray", breaks=200, xaxt="n", xlab="cpm/(μSv/h)")
tic = c(10,100,1000,10000,100000); axis(1, at=log10(tic), labels=tic)
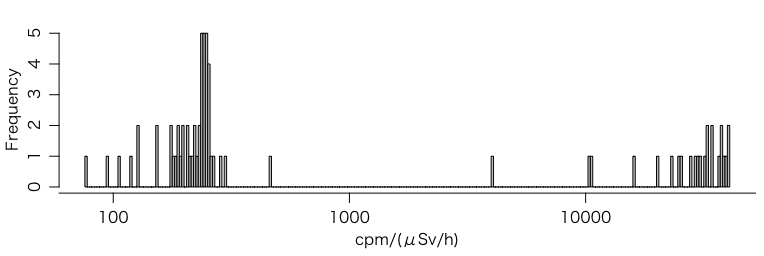
> median(s[s < 1000], na.rm=TRUE) # 左半分の中央値
[1] 230.7817
> median(s[s > 1000], na.rm=TRUE) # 右半分の中央値
[1] 31498.54
…と計算したところで,一部の機器は測定間隔が60分であることを教えていただいた。その場合は10で割っているところを60で割らなければならない。ちゃんと時間間隔も調べて計算し直す必要がある。