かなり前(最終更新日2012-08-12)にざっと書いて放置していたページを少しずつ更新しています。ロジスティック回帰と変数選択もご覧ください。
100点満点の模擬テストを20人が受験しました。点数は次の通りです:
x = c(4,5,17,17,19,19,29,41,45,47,49,54,56,58,70,76,88,88,93,97)
この20人がその後実際の試験を受験して,合否が判明しました。合 = 1,否 = 0 で表すと,次のようになりました:
y = c(0,0,0,0,0,0,1,1,1,0,0,1,1,0,1,1,1,1,1,1)
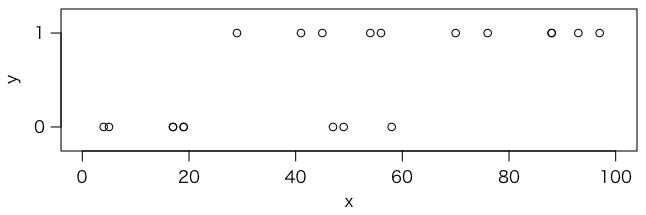
プロットしてみましょう:
plot(x, y, xlim=c(0,100), ylim=c(-0.2,1.2), yaxt="n") axis(2, at=c(0,1), labels=c(0,1), las=1)

x から y を予測する式を求めたいのですが,通常の線形回帰ではうまくあてはまりません:
r = lm(y ~ x) abline(r)
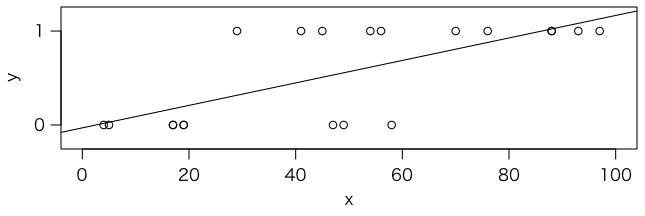
そもそもこれでは何を予測したいのかはっきりしません。予測するものを,模擬テストの点数が x のときの合格確率だとしましょう。確率は負になったり 1 を超えたりしませんので,線形回帰ではうまくありません。うまく 0 から 1 の範囲におさまってくれる関数はないでしょうか。
例えば
\[ y = \frac{1}{1 + \exp(-x)} = \frac{1}{1 + e^{-x}} \]はどうでしょうか。これをグラフにすると,次のようになります:
curve(1 / (1 + exp(-x)), -5, 5)
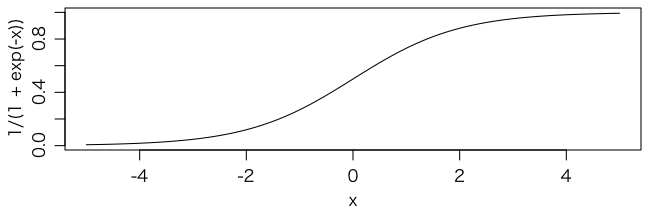
これなら縦軸の値は必ず 0 から 1 の範囲に収まりますので,確率と解釈することができます。実際には,このグラフの中心(変曲点の位置)と曲がり具合とを変えられるようにした
\[ y = \frac{1}{1 + \exp(-(w_0 + w_1 x))} \]という式で表される曲線を使うことにします。
この形の曲線をロジスティック曲線といいます。より一般に,0 から 1 に滑らかに変化する S 字形をつぶしたような曲線をシグモイド曲線といいます。シグモイド曲線は,ニューラルネットの活性化関数として使われてきました(現在は ReLU の類を使うのが普通です)。
$x$ が与えられたとき $y = 1$ になる確率 $p$ が
\[ p = \frac{1}{1 + \exp(-(w_0 + w_1 x))} \]で近似できるような係数 $w_0$,$w_1$ を求める方法をロジスティック回帰といいます。この式を書き直すと
\[ \log\left(\frac{p}{1-p}\right) = w_0 + w_1 x \]となりますが,この左辺に現れる $p$ の関数をリンク関数といいます。この場合のリンク関数はロジット関数と呼ばれ,$\mathrm{logit}(p)$ と書くことがあります。ちなみに $p/(1-p)$ はオッズ(odds)と呼ばれる量ですので,ロジット関数はオッズの対数ということになります。
R ではロジスティック回帰は次のように打ち込むと簡単にできます:
r = glm(y ~ x, family=binomial(link="logit")) summary(r)
結果は次のようになります:
Call:
glm(formula = y ~ x, family = binomial(link = "logit"))
Deviance Residuals:
Min 1Q Median 3Q Max
-1.7368 -0.4784 0.1618 0.5249 1.6902
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -3.56668 1.68570 -2.116 0.0344 *
x 0.08319 0.03562 2.335 0.0195 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 27.526 on 19 degrees of freedom
Residual deviance: 15.187 on 18 degrees of freedom
AIC: 19.187
Number of Fisher Scoring iterations: 5
この結果の Coefficients の Estimate のところに係数 $w_0$,$w_1$ が出ます。つまり,
\[ P = \frac{1}{1 + \exp(-(-3.56668 + 0.08319 x))} \]ということになります。元のデータとこの確率を重ねてグラフにしてみます:
plot(x, y, xlim=c(0,100), ylim=c(-0.2,1.2), yaxt="n") axis(2, at=c(0,1), labels=c(0,1), las=1) curve(1 / (1 + exp(-(0.08319 * x - 3.56668))), add=TRUE)
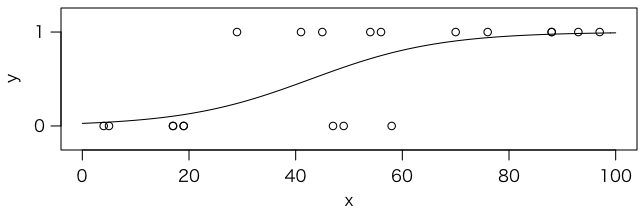
fitted(r) と打ち込めば,各人の合格確率が表示されます:
1 2 3 4 5 6 7
0.03790860 0.04106194 0.10409750 0.10409750 0.12066687 0.12066687 0.23971136
8 9 10 11 12 13 14
0.46107354 0.54406673 0.58494310 0.62468280 0.71614238 0.74871671 0.77870804
15 16 17 18 19 20
0.90520067 0.94022405 0.97710680 0.97710680 0.98477823 0.98903950
次の表を考えましょう。ここで $y$ は入試の合否(合格なら1,不合格なら0),$x_1$ は内申点,$x_2$ は模試偏差値を表すとします。
| $y$ | $x_1$ | $x_2$ |
|---|---|---|
| 0 | 3.6 | 60.1 |
| 1 | 4.1 | 52.0 |
| 0 | 3.7 | 62.5 |
| 0 | 4.9 | 60.6 |
| 1 | 4.4 | 54.1 |
| 0 | 3.6 | 63.6 |
| 1 | 4.9 | 68.0 |
| 0 | 4.8 | 38.2 |
| 1 | 4.1 | 59.5 |
| 0 | 4.3 | 47.3 |
さきほどと同様に,$x_1$,$x_2$ が与えられたとき $y = 1$ になる確率 $p$ が
\[ p = \frac{1}{1 + \exp(-(w_0 + w_1 x_1 + w_2 x_2))} \]で近似できるようにパラメータ $w_1$,$w_2$ を定めます。
次のように打ち込むとデータが data1 に読み込まれます:
data1 = read.csv("https://okumuralab.org/~okumura/stat/data1.csv")
このデータについてロジスティック回帰を行うには
r2 = glm(y ~ x1 + x2, data=data1, family=binomial(link="logit"))
と打ち込みます。続いて
summary(r2)
と打ち込めば次のように表示されます:
Call:
glm(formula = y ~ x1 + x2, family = binomial(link = "logit"),
data = data1)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.4754 -0.8584 -0.8007 1.1905 1.5719
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -9.44589 9.12237 -1.035 0.300
x1 1.27158 1.49423 0.851 0.395
x2 0.06424 0.08739 0.735 0.462
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 13.460 on 9 degrees of freedom
Residual deviance: 12.345 on 7 degrees of freedom
AIC: 18.345
Number of Fisher Scoring iterations: 4
つまり $\mathrm{logit}(\pi) = -9.44589 + 1.27158x_1 + 0.06424x_2$ で予測されることがわかります(ただしどの係数も有意ではありません)。
また,fitted(r2) と打ち込むと,フィットされた値 $\mathrm{logit}^{-1}(w_0 + w_1 x_1 + w_2 x_2)$ が表示されます。
R で「iris」と打ち込んでみてください。次のような150行のデータが現れます:
Sepal.Length Sepal.Width Petal.Length Petal.Width Species
1 5.1 3.5 1.4 0.2 setosa
2 4.9 3.0 1.4 0.2 setosa
3 4.7 3.2 1.3 0.2 setosa
...
これは有名な Fisher の iris(あやめ)のデータです。3種類の iris(setosa,versicolor,virginica)それぞれ50個ずつについて,sepal length(萼(がく)の長さ),sepal width(萼(がく)の幅),petal length(花びらの長さ),petal width(花びらの幅)が与えられています(単位は cm)。
> sapply(iris[1:4], function(x) sapply(split(x, iris$Species), mean))
Sepal.Length Sepal.Width Petal.Length Petal.Width
setosa 5.006 3.428 1.462 0.246
versicolor 5.936 2.770 4.260 1.326
virginica 6.588 2.974 5.552 2.026
例えば萼と花びらの長さをプロット:
plot(iris$Sepal.Length, iris$Petal.Length, col=iris$Species)
legend("bottomright", legend=levels(iris$Species), pch=1, col=1:3)
主成分分析をするのも手です:
r = prcomp(iris[1:4])
plot(r$x[,1], r$x[,2], col=iris$Species)
legend("topright", legend=levels(iris$Species), pch=1, col=1:3)
ロジスティック回帰で,これら4つの変数から,まずは setosa かそれ以外かを判別してみましょう。
ヒント:iris というデータに setosa という列を追加して,Species が setosa なら 1,そうでないなら 0 とする命令:
iris$setosa = ifelse(iris$Species == "setosa", 1, 0)
残りは課題です。
次の表は,Annette J. Dobson and Adrian G. Barnett, An Introduction to Generalized Linear Models, 3rd ed. (CRC Press, 2008) の p.127 にあるデータです。$x$ はある薬品の量(対数),$n$ はその薬品を与えたカブトムシの数,$y$ はそのうち死んだ数です。薬品の量が増えると死ぬ確率がどのように高くなるかを調べます。
| $x$ | $n$ | $y$ |
|---|---|---|
| 1.6907 | 59 | 6 |
| 1.7242 | 60 | 13 |
| 1.7552 | 62 | 18 |
| 1.7842 | 56 | 28 |
| 1.8113 | 63 | 52 |
| 1.8369 | 59 | 53 |
| 1.8610 | 62 | 61 |
| 1.8839 | 60 | 60 |
モデルは $\mathrm{logit}(\pi) = w_0 + w_1 x$ で,確率 $\pi$ はほぼ $y/n$ になるはずです。
さきほどと同様にしてデータ(data2.csv)を data2 に読み込んで,次のように打ち込みます。
r3 = glm(cbind(y,n-y) ~ x, data=data2, family=binomial(link="logit"))
関数 glm() に与えるモデル式の左辺は,成功した個数のベクトル $y$ と失敗した個数のベクトル $n - y$ をコラム結合 cbind() した8行2列の行列です。
summary(r3) と打つと次のような結果が表示されます:
Call:
glm(formula = cbind(y, n - y) ~ x, family = binomial(link = "logit"),
data = data2)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.5941 -0.3944 0.8329 1.2592 1.5940
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -60.717 5.181 -11.72 <2e-16 ***
x 34.270 2.912 11.77 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 284.202 on 7 degrees of freedom
Residual deviance: 11.232 on 6 degrees of freedom
AIC: 41.43
Number of Fisher Scoring iterations: 4
関数 glm() の名前は一般化線形モデル(generalized linear model,GLM)から来ています。family= で指定できる確率分布およびリンク関数のおもなものを挙げておきます:
binomial(link="logit")binomial(link="probit")binomial(link="cauchit")binomial(link="log")binomial(link="cloglog")gaussian(link="identity")gaussian(link="log")gaussian(link="inverse")Gamma(link="inverse")Gamma(link="identity")Gamma(link="log")inverse.gaussian(link="1/mu^2")inverse.gaussian(link="inverse")inverse.gaussian(link="identity")inverse.gaussian(link="log")poisson(link="log")poisson(link="identity")poisson(link="sqrt")quasi(link="identity", variance="constant")quasibinomial(link="logit")quasipoisson(link="log")詳しくは glm や family のヘルプをご覧ください。
より収束しやすい glm2 というパッケージが開発されています。詳しくは The R Journal, Volume 3/2 の Ian C. Marschner, “glm2: Fitting Generalized Linear Models with Convergence Problems” というペーパーをご覧ください(オープンアクセスです)。
Rで多項ロジスティック回帰をするパッケージはいくつかあるようですが,ここではVGAMパッケージをご紹介しておきます。詳しくは Thomas W. Yee, The VGAM Package for Categorical Data Analysis, Journal of Statistical Software, Vol.32, No.10 (2010) をご覧ください。
Last modified: