$n$ 人について $m$ 個の変数を測定した。$i$ 番の人の $j$ 番の変数の値を $x_{ij}$ とする。また,$i$ 番の人がある性質を満たすならば $y_i = 1$,そうでなければ $y_i = 0$ で表す。ここで $y_i$ を $x_{ij}$ から予測するのが問題である。具体的には,模擬試験や内申書の成績から入試の合否を予測する問題や,性別・年齢・血圧などから病気を予測する問題がこれである。
このように結果が 0 か 1 かに限られる場合は,結果が 1 となる確率 $p_i$ を $x_{ij}$ についての線形の式で予測することが考えられる。しかし,確率は $0 \leq p_i \leq 1$ の範囲に限られるので,
\[ \mathrm{logit}(p) = \log \frac{p}{1-p}, \qquad p = \mathrm{logit}^{-1}(x) = \frac{e^x}{1 + e^x} \]という関数を考えて,
\[ \mathrm{logit}(p_i) = \sum_{j=1}^m b_j x_{ij} + c_j \]という式で予測する。変数 $y_i$ は,確率 $p_i$ で 1 になり,確率 $1 - p_i$ で 0 になる2項分布をすると考える。このような予測式を作ることをロジスティック回帰という。
まず例題用のデータを乱数で作る。ここでは次のようにして100人×10個の説明変数と1個の目的変数とを作った:
set.seed(1)
x = matrix(round(rnorm(1000,mean=50,sd=10)), ncol=10)
invlogit = function(x){exp(x)/(1+exp(x))}
y = sapply(1:100, function(i){rbinom(1, 1, invlogit((x[i,]-50) %*% (1:10)/100))})
実際のロジスティック回帰は次のコマンドで行う:
r1 = glm(y ~ x[,1] + x[,2] + x[,3] + x[,4] + x[,5] + x[,6] + x[,7] + x[,8] + x[,9] + x[,10],
family=binomial(link="logit"))
結果は r1 に入る。そのサマリーを出力させる:
> summary(r1)
Call:
glm(formula = y ~ x[, 1] + x[, 2] + x[, 3] + x[, 4] + x[, 5] +
x[, 6] + x[, 7] + x[, 8] + x[, 9] + x[, 10], family = binomial(link = "logit"))
Deviance Residuals:
Min 1Q Median 3Q Max
-2.63394 -0.50453 -0.05924 0.44280 2.00046
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -37.75406 8.42380 -4.482 7.4e-06 ***
x[, 1] 0.03587 0.03833 0.936 0.349244
x[, 2] -0.01386 0.03479 -0.398 0.690441
x[, 3] 0.04029 0.02963 1.360 0.173892
x[, 4] 0.08904 0.03645 2.443 0.014576 *
x[, 5] 0.09239 0.03604 2.564 0.010356 *
x[, 6] 0.11091 0.03796 2.922 0.003480 **
x[, 7] 0.05678 0.03159 1.798 0.072239 .
x[, 8] 0.09457 0.03746 2.524 0.011591 *
x[, 9] 0.15957 0.04533 3.520 0.000432 ***
x[, 10] 0.08699 0.03274 2.657 0.007889 **
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 138.269 on 99 degrees of freedom
Residual deviance: 69.291 on 89 degrees of freedom
AIC: 91.291
Number of Fisher Scoring iterations: 6
係数は非常に有意なもの(***)からまったく有意でないもの(無印)まで多様である。そこで,有意でない変数を外していけば,予測式はより安定する。どれくらい良い予測式であるかを評価するための指標はいろいろ考えられるが,ここではAIC(赤池情報量規準,An Information Criterion,Akaike's Information Criterion)という数値が使われている。
あまり関係なさそうな変数を手作業で除いていってもよいが,自動化するには,step() という関数を使う:
r2 = step(r1)
これは,デフォルトではフルモデルから1個ずつ変数を外すことを試み,外すと一番AICが良く(小さく)なるものを実際に外す。外すことによってAICが改善しなくなるまで続ける。最終的には変数 2,1,3 がこの順に外され,変数 4〜10 が残る。その時点でのAICは 87.92 である。
変数 4〜10 が残った時点であらためて計算してみる:
r3 = glm(y ~ x[,4] + x[,5] + x[,6] + x[,7] + x[,8] + x[,9] + x[,10],
family=binomial(link="logit"))
summary(r3)
結果は次のようになる:
Call:
glm(formula = y ~ x[, 4] + x[, 5] + x[, 6] + x[, 7] + x[, 8] +
x[, 9] + x[, 10], family = binomial(link = "logit"))
Deviance Residuals:
Min 1Q Median 3Q Max
-2.17312 -0.53009 -0.09058 0.46361 1.96882
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -32.42913 6.80960 -4.762 1.91e-06 ***
x[, 4] 0.08389 0.03498 2.398 0.016464 *
x[, 5] 0.08887 0.03315 2.681 0.007347 **
x[, 6] 0.10510 0.03747 2.805 0.005035 **
x[, 7] 0.05809 0.02937 1.978 0.047950 *
x[, 8] 0.08352 0.03587 2.328 0.019893 *
x[, 9] 0.15230 0.04363 3.491 0.000482 ***
x[, 10] 0.07626 0.02950 2.585 0.009733 **
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 138.269 on 99 degrees of freedom
Residual deviance: 71.922 on 92 degrees of freedom
AIC: 87.922
Number of Fisher Scoring iterations: 6
つまり,予測式は次のようになる:
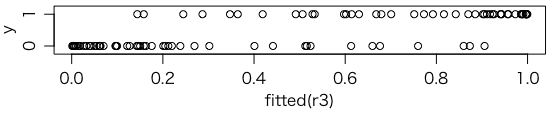
\[ \mathrm{logit}(p_i) = 0.08389 x_{i4} + 0.08887 x_{i5} + \cdots + 0.07626 x_{i,10} - 32.42913 \]この予測式から求めた $p_i$ は fitted() という関数で求められる。これを横軸に,実際の値 $y_i$ を縦軸にとってプロットすると次のようになる:
plot(fitted(r3), y, ylim=c(-0.2,1.2), yaxt="n")
axis(2, c(0,1))
なお,fitted(r3) は invlogit(predict(r3)) とも書ける。

ROC曲線も描いてみる:
> ROC(fitted(r3), y)
AUC = 0.9189081 th = 0.2447937
BER = 0.1533521 OR = 62.67857
Actual
Predicted 0 1
FALSE 39 2
TRUE 14 45
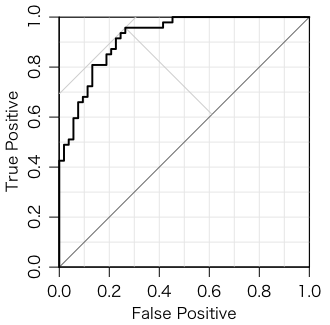
th = 0.2447937 は上の図の上段($y_i = 1$)の左から3番目の点の横座標($p_i$)である。この点を含めてその右側を 1 と予測すれば,上段の左側2個は偽陰性(false negative),下段の右側14個は偽陽性(false positive)になる。この点は,偽陰性率 $2/47$ と偽陽性率 $14/53$ の平均(Balanced Error Rate,BER)を最小にする点である。このとき,オッズ比(odds ratio,OR)は $(39/2)/(14/45) = 62.67857$ になる。この点を予測のしきい値とするのがベストというわけではなく,偽陰性率(間違って0だと予測してしまう率)と偽陽性率(間違って1だと予測してしまう率)を天秤にかけて決めればよい。
場合によっては glm() が警告メッセージを出す:
警告メッセージ:
1: glm.fit: アルゴリズムは収束しませんでした
2: glm.fit: 数値的に 0 か 1 である確率が生じました
ここで r1 を表示してみると,本当に 0 か 1 の値になってしまっている。こういう「完全な予測」は,人工データで起きることがあるようだ。きちんと予測できるなら,これでも問題ないだろう。
なお,通常の線形回帰分析 lm() でも同様の変数選択が行える。
r1 = lm(y ~ x[,1] + x[,2] + x[,3] + x[,4] + x[,5] + x[,6] + x[,7] + x[,8] + x[,9] + x[,10])
r2 = step(r1)
...
step() は変数のサブセットを全部試してくれるわけではない。全部試したければ,bestglm() を使う:
> install.packages("bestglm")
> library(bestglm)
> Xy = data.frame(x, y)
> bestglm(Xy, family=binomial(link="logit"), IC="AIC")
AICだけでなく,BICやCV(cross-validation)などもできる。ただし,変数が多いと時間がかかる。
Last modified: