未定原稿です。
ある薬の効果を調べたら $p < 0.05$ で有意だった。有意差でた! よかった♡
でも,これでは,$p = 0.049$ なのか $p = 0.0000001$ なのかわからない。どうせ $p$ 値を書くのなら,$p < 0.05$ のような不等式ではなく,具体的に $p = 0.023$ などと書くほうがよい(例えば Publication Manual of the American Psychological Association 参照)。
さらに言えば,そもそも,$p$ 値は効果の大きさを表す量ではない。具体的に,例えば「高血圧症の人の収縮期血圧が平均 5mmHg だけ下がった。95% 信頼区間は [1, 9] だった」と書くほうがよい([1, 9] は $1 \leq x \leq 9$ の範囲の $x$ という意味)。これで効果の大きさがわかるし,信頼区間を見れば,「効果がない」という帰無仮説が $p < 0.05$ で棄却されることもわかる。
別の例:「この勉強法を使うと,学校の試験の成績が偏差値にして平均2ポイント上がった。95% 信頼区間は [0, 4] だった」。これは,効果が 0 という帰無仮説を捨てる・捨てないの境目にある。
このように,具体的な血圧とか偏差値とか,つまり効果量(effect size)と,その信頼区間とを報告しようというのが時代の流れである($p$ 値も報告してよいが 95% 信頼区間を見れば $p < 0.05$ で有意かどうかはすぐわかる)。
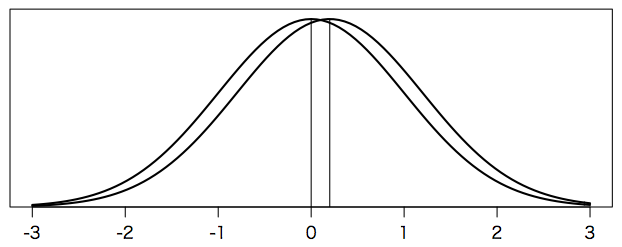
偏差値の標準偏差は 10 である(偏差値の定義より)。したがって,偏差値が2ポイント改善したということは,標準偏差の 0.2 倍だけ改善したということである。この「標準偏差の何倍」という値を Cohen(コーエン)の $d$ という。この勉強法による効果が Cohen の $d = 0.2$ だといえば,偏差値が 2 だけ上がったことになる。偏差値の平均は 50 であるから,この勉強法をした人の偏差値は平均 52 になったわけである。次の図を見ても,$d = 0.2$ は,ほんのわずかである。

par(mgp=c(2,0.8,0)) # 軸マージン(デフォルト: c(3,1,0))
par(mar=c(2,0.5,0.5,0.5))
curve(dnorm(x), lwd=2, xlim=c(-3,3), ylim=c(0,0.42),
xlab="", ylab="", yaxt="n", yaxs="i")
curve(dnorm(x,mean=0.2), lwd=2, add=TRUE)
segments(0, 0, 0, dnorm(0))
segments(0.2, 0, 0.2, dnorm(0))
Facebookでニュースフィードのポジティブなポストとネガティブなポストの割合をユーザごとに変えたところ,そのユーザの書き込みもそれに応じてポジティブ・ネガティブな語の割合が変わったという論文 Experimental evidence of massive-scale emotional contagion through social networks が2014年に話題になったが,そのときの効果量は Cohen's $d = 0.02$ だった。偏差値にして 0.2 ポイントの違いで,次のグラフのように,ほとんど重なってしまう。それでもFacebookのユーザはとても多いので $p < 0.001$ で有意となる。$p$ 値だけを見て,すごい効果があると勘違いしてはならない。効果量を見なければならない。
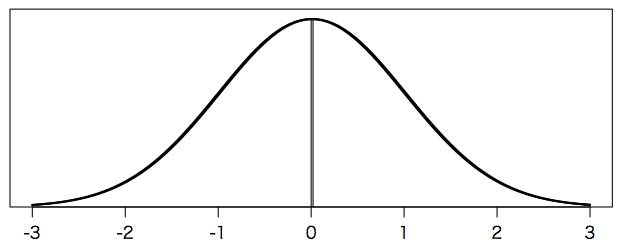
curve(dnorm(x), lwd=2, xlim=c(-3,3), ylim=c(0,0.42),
xlab="", ylab="", yaxt="n", yaxs="i")
curve(dnorm(x,mean=0.02), lwd=2, add=TRUE)
segments(0, 0, 0, dnorm(0))
segments(0.02, 0, 0.02, dnorm(0))
Cohen's $d = 0.02$ の違いはFacebook規模でないと示すのは難しそうなので,$d = 0.2$ の違いを考えよう。それでも,このページの最初の図のように,かなり重なっている。でも,$N$ 人を集めれば,その平均の分散は $1/N$ になる。処理をした群(実験群)と,何もしない群(対照群)をそれぞれ $N$ 人集めれば,平均の差の分散は $2/N$ になる。$N = 200$ なら差の分散は 1/100,標準偏差にすれば 1/10 になる。$d = 0.2$ は元の標準偏差の 0.2 倍であったが,200人の差の標準偏差の 2 倍になり,正規分布なら 1.96 以上なので $p < 0.05$ で有意である。実際には $t$ 分布(自由度 398)を使うから 1.960 でなく 1.966 が境目だが,たいした違いではないので,以下では正規分布で話を進める。
もともとの Cohen's $d$ は,両群の平均値の差を,両群を合わせた(プールした)標準偏差 $\sqrt{((n_1-1)s_1^2 + (n_2-1)s_2^2) / (n_1 + n_2 - 2)}$ で割ったものである。これには若干のバイアスがある。通常は気にすることはないが,補正するには $d$ に $1 - 3 / (4(n_1+n_2)-9)$ を掛ける。この補正を掛けた値を Hedges's $g$ と呼ぶ。
Cohen's $d$ は,Rのパッケージ effsize で求めることができる。
cohen.d(x, y, hedges.correction=TRUE)
のようなオプションを与えるとHedgesの補正をする。
一方,標準偏差をプールしないで,基準となる群(対照群)の標準偏差を基準とすべきであるという議論もある。こうして求めたものを Glass's $\Delta$ ということがある。
次の図は標準正規分布の $\pm 1.96$ とその外側の領域である。ここに入れば危険率 $\alpha = 0.05$ で帰無仮説を棄却するというのが(後述の $\beta$ も含めて)通常の(Neyman-Pearson 流の)統計学の考え方である。この $\alpha = 0.05$ は「帰無仮説 $H_0$ が正しいのに $H_0$ を棄却してしまう確率」である。
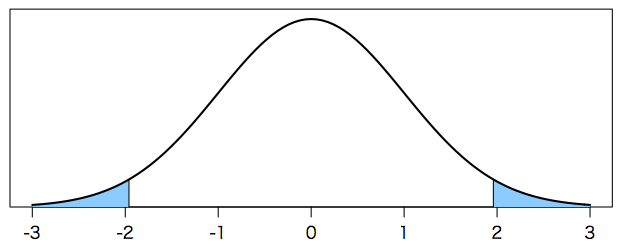
plot(NULL, xlim=c(-3,3), ylim=c(0,0.42), xlab="", ylab="", yaxt="n", yaxs="i")
x = -1.96-(0:10)/10*(3-1.96)
y = dnorm(x)
polygon(c(x,x[length(x)],x[1]), c(y,0,0), col="#66ccff", border=NA)
x = 1.96+(0:10)/10*(3-1.96)
y = dnorm(x)
polygon(c(x,x[length(x)],x[1]), c(y,0,0), col="#66ccff", border=NA)
segments(-1.96, 0, -1.96, dnorm(-1.96))
segments(1.96, 0, 1.96, dnorm(1.96))
curve(dnorm(x), lwd=2, add=TRUE)
ところで,真の効果量(標本誤差を含まない)が例えば $\mu = 2$ のところにあったとしよう(母集団の平均を $\mu$ で表す)。この仮説を,帰無仮説 $H_0$ と対比させて,対立仮説 $H_1$ と呼ぶ(もちろん対立仮説は無数にあるが,その一つを考えている)。これはさきほどの帰無仮説を棄却する範囲に入っているが,実際の測定値(標本誤差を含む)は $x = 2$ のまわりに下の図のように分布するので,帰無仮説を棄却できない可能性(つまり実際の測定値が図のオレンジ色の部分に入る確率 $\beta$)はほぼ 1/2 である。この $\beta$ は「対立仮説 $H_1$ が正しいのに帰無仮説 $H_0$ を棄却できない確率」である。
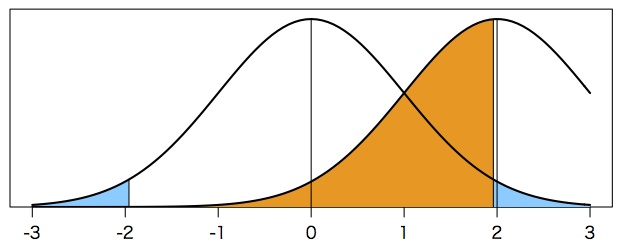
plot(NULL, xlim=c(-3,3), ylim=c(0,0.42), xlab="", ylab="", yaxt="n", yaxs="i")
x = -1.96-(0:10)/10*(3-1.96)
y = dnorm(x)
polygon(c(x,x[length(x)],x[1]), c(y,0,0), col="#66ccff", border=NA)
x = 1.96+(0:10)/10*(3-1.96)
y = dnorm(x)
polygon(c(x,x[length(x)],x[1]), c(y,0,0), col="#66ccff", border=NA)
segments(-1.96, 0, -1.96, dnorm(-1.96))
x = 1.96-(0:20)/20*(1.96+2)
y = dnorm(x,mean=2)
polygon(c(x,x[length(x)],x[1]), c(y,0,0), col="#ff9900", border=NA)
segments(1.96, 0, 1.96, dnorm(1.96,mean=2))
segments(0, 0, 0, dnorm(0))
curve(dnorm(x), lwd=2, add=TRUE)
segments(2, 0, 2, dnorm(0))
curve(dnorm(x,mean=2), lwd=2, add=TRUE)
この対立仮説 $H_1$ による測定値の分布($\mu = 2$ のまわりの分布)のうち $\beta$ 以外の部分,つまり「対立仮説 $H_1$ が正しいと仮定して帰無仮説 $H_0$ が棄却される確率」$1 - \beta$ を「検出力(検定力)」(power)と呼ぶ。下の図の緑の部分の面積が検出力に相当する。本当は $x \leq -1.96$ のところにも緑の部分があるが,ほとんど 0 であり,見えない。
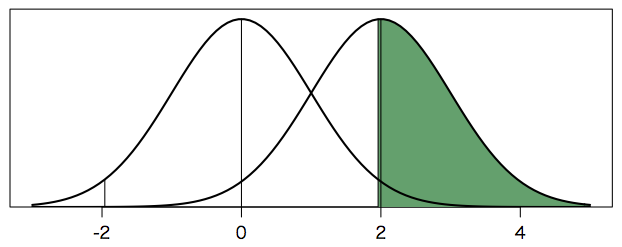
plot(NULL, xlim=c(-3,5), ylim=c(0,0.42), xlab="", ylab="", yaxt="n", yaxs="i")
segments(-1.96, 0, -1.96, dnorm(-1.96))
x = 1.96+(0:20)/20*(5-1.96)
y = dnorm(x,mean=2)
polygon(c(x,x[length(x)],x[1]), c(y,0,0), col="#35a16b", border=NA)
segments(1.96, 0, 1.96, dnorm(1.96,mean=2))
segments(0, 0, 0, dnorm(0))
curve(dnorm(x), lwd=2, add=TRUE)
segments(2, 0, 2, dnorm(0))
curve(dnorm(x,mean=2), lwd=2, add=TRUE)
検出力は,実験をする前に,想定される対立仮説 $H_1$ について,計画している実験(例えば被験者の数 $N$)で十分かどうかを調べるために計算するものである。検出力が小さければ,もっと $N$ を増やすことを考えればよい。
そういうわけで,「検出力を計算しよう」という流れが生じたが,実際問題として,実験をする前に効果量の真の値を見積もるのは困難である。そこで,実験をした後に,得られた測定値 $x$ を対立仮説の母集団の平均値 $\mu$ と見なして,事後的に求めた検出力を報告することが一部で行われている。しかし,これでは,例えば上の図のように $\alpha = 0.05$ で $p = 0.05$ なら必ず $1 - \beta = 1/2$ であるという具合に,得られた $p$ 値によって定まる値を求めているに過ぎず,意味がよくわからない。この点について詳しく論じた次の論文を参照されたい(タイトルでネット検索すればPDFが見つかる)。
$\alpha$ や $\beta$ や検出力は Neyman-Pearson 流の考え方に深く根ざしている。一方で,科学者が最終的に知りたいのは,具体的な量(効果量)とその不確かさ(信頼区間)である。その意味では,検出力より,事前にいくつかの場合を想定してシミュレーションにより効果量と不確かさを求めてみるほうがわかりやすい。
以上について参考になる本(非常に平易):
上の本の要約的なもの。PDFが無料でダウンロードできる:
次の図は,平均 $\mu = 0$ と $\mu = 3.29$,標準偏差 $\sigma = 1$ の二つの正規分布を描いたもので,帰無仮説 $H_0$: $\mu = 0$ に対して,片側 5%($x \geq 1.645$,図の空色の部分)に棄却域を設定したとき,対立仮説 $H_1$: $\mu = 1.645 \times 2 = 3.29$ に対して $\alpha = \beta = 0.05$ が得られることを示したものである。つまり,真の値が $\mu = 3.29$ であれば,誤差のために測定値がふらついたとしても,95% の確率で $x \geq 1.645$ の棄却域に測定値が入る。ここまでは正しい。
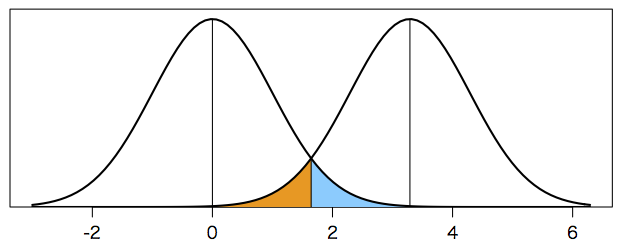
plot(NULL, xlim=c(-3,1.644854*2+3), ylim=c(0,0.42), xlab="", ylab="", yaxt="n", yaxs="i")
x = 1.644854+(0:10)/10*(3.5-1.644854)
y = dnorm(x)
polygon(c(x,x[length(x)],x[1]), c(y,0,0), col="#66ccff", border=NA)
x = 1.644854-(0:10)/10*(3.5-1.644854)
y = dnorm(x,mean=1.644854*2)
polygon(c(x,x[length(x)],x[1]), c(y,0,0), col="#ff9900", border=NA)
segments(1.644854, 0, 1.644854, dnorm(1.644854,mean=1.644854*2))
segments(0, 0, 0, dnorm(0))
curve(dnorm(x), lwd=2, add=TRUE)
segments(1.644854*2, 0, 1.644854*2, dnorm(0))
curve(dnorm(x,mean=1.644854*2), lwd=2, add=TRUE)
このような $\alpha$ と $\beta$ を同時に制御する点を minimum detectable activity (MDA) あるいは minimum detectable concentration (MDC) などと呼ぶ。これは Lloyd A. Currie(キュリー Curie ではなくカーリー Currie)による考え方のようで,よく誤解されて,誤検出の確率を 5% に抑えるには測定値が $3.29\sigma$ 以上でなければならないといわれることがある。これはまったくの間違いで,誤検出の確率を片側 5% に抑えたければ単純に $1.645\sigma$ で区切ればよい。
Currie の書いたものはネット上でもいくつか見つかるが,考え方の解説として,上本道久「検出限界と定量下限の考え方」がわかりやすい。なお,Currie の $\sigma$ はブランク(空試験値)の標準偏差であり,測定誤差とは微妙に違う。
いずれにせよ,放射性物質の検査では,検出限界未満の値は「ND」(Not Detected),検出限界以上の値は(信頼区間でなく)値をそのまま(誤差の程度も示さずに)報告する習慣が定着してしまった。
一つ一つがNDであっても,いくつか集まれば有意な情報が得られることがある(メタアナリシス参照)。平時の科学研究モードに戻れば,値と誤差(あるいは信頼区間)が報告されるようになるのだろうか。
Last modified: