分散分析

一元配置分散分析

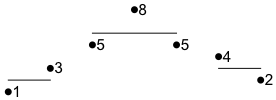
右の図は，3グループ（2点，3点，2点）に分かれた7点のデータ $x = (1,3,5,8,5,4,2)$ を示したものです。Rの書き方では

x = c(1,3,5,8,5,4,2)          # データ
g = factor(c(1,1,2,2,2,3,3))  # グループの分かれ方

ということになります。図の横棒は各グループの平均（それぞれ 2，6，3）です。

plot(1:7, x, pch=16, xlab="", ylab="", axes=FALSE)
text((1:7)+0.2, x, x)
lines(c(1,2), c(2,2))
lines(c(3,5), c(6,6))
lines(c(6,7), c(3,3))

元のデータ $x$ は7個の値から成りますので，自由度が7個です（$x$ has seven degrees of freedom）。

各値をグループの平均で置き換えたものは，自由度が3個です：

y = ave(x, g)
y
[1] 2 2 6 6 6 3 3

aggregate(x, by=list(g), FUN=mean)
  Group.1 x
1       1 2
2       2 6
3       3 3

全部の値を全体の平均4で置き換えたものは，自由度が1個です：

z = ave(x)
z
[1] 4 4 4 4 4 4 4

$y$ から $z$ を引いたもの

y - z
[1] -2 -2  2  2  2 -1 -1

は，自由度 $3 - 1 = 2$ です。異なった値が3個なので自由度3のように見えますが，全部の合計が 0 に固定されていますので，自由度が一つ少ないのです。この2乗和（平方和）は 22 です：

sum((y - z)^2)
[1] 22

この値は，グループ内での変動を消してグループ間の変動だけにしたものの2乗和ですので，群間平方和（級間平方和）sum of squares between groups の意で $SS_\text{between}$ と書くことにします。

$x$ が標準正規分布なら，この2乗和の分布は自由度 2 のカイ2乗分布です。

同様に，$x$ から $y$ を引いたもの

x - y
[1] -1  1 -1  2 -1  1 -1

は，自由度 $7 - 3 = 4$ です。7個の値がありますが，最初の2個の和は 0，次の3個の和も 0，最後の2個の和も 0 という3個の条件があるので，自由度が3個減っています。この2乗和は 10 です：

sum((x - y)^2)
[1] 10

この値は，さきほどとは逆に，グループ内での変動だけを取り出したものの2乗和ですので，群内平方和（級内平方和）sum of squares within groups の意で $SS_\text{within}$ と書くことにします。

$x$ が標準正規分布なら，この2乗和の分布は自由度 4 のカイ2乗分布です。

ベクトル $x - y$ と $y - z$ は直交します（なぜならば $y - z$ の同じ値の成分が続くグループ内で $x - y$ の成分の和は0だから，内積をとると0になります）ので，それらの2乗和の和は $x - z$ の2乗和になります：

sum((x - z)^2)
[1] 32

これを $SS_\text{total}$ と書くことにします。つまり，

ということになります。ここで，比

(sum((y-z)^2) / 2) / (sum((x-y)^2) / 4)
[1] 4.4

を考えます。分子 (sum((y-z)^2) / 2) は $SS_\text{between}$ をその自由度2で割ったもので，分母 (sum((x-y)^2) / 4) は $SS_\text{within}$ をその自由度4で割ったものです。ここでもし $x$ の分布が正規分布なら，この比の分布は自由度 (2,4) の $F$ 分布です（下の「復習」参照）。したがって，

1 - pf(4.4, 2, 4)
[1] 0.09765625

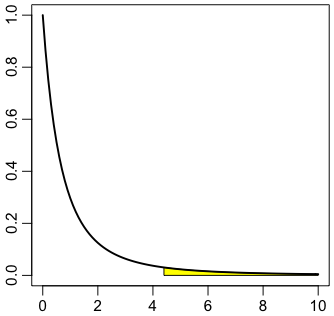で上側確率が出ます。つまり，比 (sum((y-z)^2) / 2) / (sum((x-y)^2) / 4) が 4.4 以上になる確率は約10%です。グループ内の変動に比べて，グループ間の変動がこれ以上に大きくなる確率は10%ほどあり，5%水準では有意といえません。

# par(mgp=c(1.8,0.6,0))
plot(NULL, xlim=c(0,10), ylim=c(0,1), xlab="", ylab="")
s = seq(4.4, 10, 0.1)
polygon(c(s,10,4.4), c(df(s,2,4),0,0), col="yellow")
curve(df(x,2,4), lwd=2, add=T)

以上のことをもっと簡単に行うのが，線形モデルをあてはめる関数 lm() と，あてはめたモデルの分散分析を行う関数 anova() です。

anova(lm(x ~ g))

結果は伝統的な分散分析表です：

Analysis of Variance Table

Response: x
          Df Sum Sq Mean Sq F value  Pr(>F)  
g          2   22.0    11.0     4.4 0.09766 .
Residuals  4   10.0     2.5                  
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 

同じ表は summary(aov(x ~ g)) でも出力できます。

Df が自由度（degrees of freedom），Sum Sq が2乗和（平方和，sum of squares），Mean Sq が2乗和を自由度で割ったもの（平均平方，mean squares），F value が $F$ の値，Pr(>F) がこの $F$ 値以上（$\geq$）の $F$ 値が出る確率（$p$ 値）です。その右側のピリオドは，下に凡例が出ていますが，$0.05 < p \leq 0.1$ であることを表します。

もっと簡潔な出力が次のコマンドで得られます：

oneway.test(x ~ g, var.equal=TRUE)

この var.equal=TRUE は分散が等しいことを仮定するという意味です。実は oneway.test() のデフォルトは，t検定 のときのWelchの方法と同じ方法で，等分散を仮定しないで分散分析をします：

oneway.test(x ~ g)

        One-way analysis of means (not assuming equal variances)

data:  x and g 
F = 3.3913, num df = 2.0, denom df = 2.4, p-value = 0.1998

なお，2群の比較の場合，分散分析と $t$ 検定は同じことです。

並べ替え検定による方法

以上は正規分布を仮定した伝統的な分散分析です。正規分布を仮定せずに，$x$ のすべての (2,3,2) 分割について，上の sum((y-z)^2) に相当するもの（グループ間の変動の2乗和）が実際の値以上になる確率を求めてみましょう（このプログラムはもっと単純にできるかもしれません）：

x = c(1,3,5,8,5,4,2)          # データ
g = factor(c(1,1,2,2,2,3,3))  # グループの分かれ方
ssq0 = sum((ave(x,g) - ave(x))^2) # 群間2乗和
c1 = combn(7, 3)
c2 = combn(4, 2)
n1 = ncol(c1)
n2 = ncol(c2)
ssq = numeric(0)
for (i in 1:n1) {
  a = c1[,i]
  g[a] = 1
  b = setdiff(1:7, a)
  for (j in 1:n2) {
    g[b[c2[,j]]] = 2
    g[b[-c2[,j]]] = 3
    ssq = append(ssq, sum((ave(x,g)-ave(x))^2))
  }
}
mean(ssq >= ssq0)

結果は 0.06666667 で，正規分布を仮定した値 0.09766 より若干小さくなりました。

復習

標準正規分布の確率変数 $X_1$, $X_2$, ..., $X_n$ が与えられたとき，その2乗和 $\chi^2_n = X_1^2 + X_2^2 + \cdots + X_n^2$ の分布を，自由度 $n$ のカイ2乗分布（$\chi^2$ 分布）といいます。

自由度 $m$ のカイ2乗分布の確率変数 $\chi^2_m$ をその自由度 $m$ で割ったものと，それと独立な自由度 $n$ のカイ2乗分布の確率変数 $\chi^2_n$ をその自由度 $n$ で割ったものの比

の分布を，自由度 $(m, n)$ の $F$ 分布といいます。

おまけ：Kruskal-Wallis 検定

上の oneway.test(x ~ g) に相当するノンパラメトリックな（分布を仮定しない）検定です：

kruskal.test(x ~ g)

	Kruskal-Wallis rank sum test

data:  x by g
Kruskal-Wallis chi-squared = 4.8, df = 2, p-value = 0.09072