空間線量率の航空機モニタリングの続編である。
放射性物質モニタリングデータ→航空機モニタリング [空間線量率]→放射性物質の分布状況等調査による無人ヘリモニタリングから「無人ヘリコプターを用いた福島第一原子力発電所から5km圏内の空間線量率の測定結果 ( H28.9~H28.10 )」の「CSV(UTF-8)」をダウンロードして解凍し,読み込む:
options(stringsAsFactors=FALSE)
mesh = read.csv("1010302010_00.csv", fileEncoding="UTF-8")
names(mesh) で項目名を調べると,7列目が北緯(10進),8列目が東経(10進),10列目が空間線量率(μSv/h)であることがわかる。 table(mesh[,10]) してわかるように,最小階級が "< 1.0E-01" であるため,全体が文字列になってしまっている。最小階級をとりあえず 0 として,数値に直す:
mesh[,10] = as.numeric(ifelse(grepl("<",mesh[,10]), "0", mesh[,10]))
シェープファイルを読むおよび空間線量率の航空機モニタリングと同様に,福島県のシェープファイルを読む:
library(sf)
fukushima = st_read("N03-180101_07_GML/", options="ENCODING=CP932")
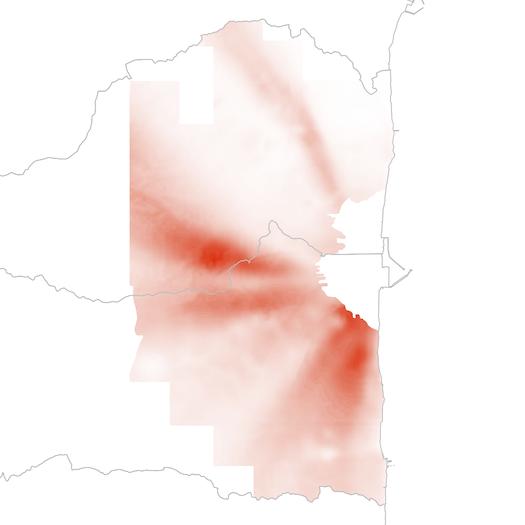
自治体境界の上に測定値を色で示す。福島第一原発の北半分は双葉町,南半分は大熊町である:
cols = colorRamp(c("white","#ff2800"))
par(mar=c(0,0,0,0)) # マージンをなくす。デフォルトは par(mar=c(5,4,4,2)+0.1)
plot(st_geometry(fukushima), xlim=range(mesh[,8]), ylim=range(mesh[,7]), border="gray")
points(mesh[,8], mesh[,7], pch=".", col=rgb(cols(pmin(pmax(mesh[,10],0)/27,1))/255))
plot(st_geometry(fukushima), border="gray", add=TRUE)

地上の測定値は放射性物質モニタリングデータ→モニタリングポスト・リアルタイム線量計→全国及び福島県の空間線量測定結果(日次平均値)の「データダウンロード」→「全国及び福島県の空間線量測定結果(リアルタイム配信)日次平均値 ( H28.4~H29.3 )」→「福島県」(1010403006_07.csv.zip)をダウンロードし,1010403006_07 というディレクトリに展開する。また,jsdfq43wtrさんの mp-maker-memo.csv も参照する。
mplist = read.csv("mp-maker-memo.csv", header=FALSE, fileEncoding="UTF-8")
files = dir(path="1010403006_07", pattern="*.csv", full.names=TRUE, recursive=TRUE)
n = length(files)
lat = lon = rad = avi = mp = rep(NA, n)
for (i in 1:n) {
a = read.csv(files[i], fileEncoding="UTF-8")
a = subset(a, 測定日 >= "2016-09-01" & 測定日 <= "2016-10-30") # H28年9・10月分を抜き出す
if (dim(a)[1] == 0) next # 空であれば次に
lat[i] = mean(a[,5])
lon[i] = mean(a[,6])
rad[i] = mean(a[,8]) # 1ヶ月分の平均線量率
d = (lat[i] - mesh[,7])^2 + (lon[i] - mesh[,8])^2
k = which.min(d) # 最近接のメッシュ点を探す
if (d[k] >= 0.00001) next
avi[i] = mesh[k,10] # メッシュ点の無人ヘリデータ
d = (lat[i] - mplist[,8])^2 + (lon[i] - mplist[,7])^2
k = which.min(d) # 最近接のモニタリングポストを探す
mp[i] = (d[k] < 0.00001)
}
plot(avi, rad, log="xy", xlim=c(0.028,16), ylim=c(0.028,16), asp=1,
pch=ifelse(mp, 4, 1), xlab="無人ヘリ", ylab="地上1m")
abline(0, 1)
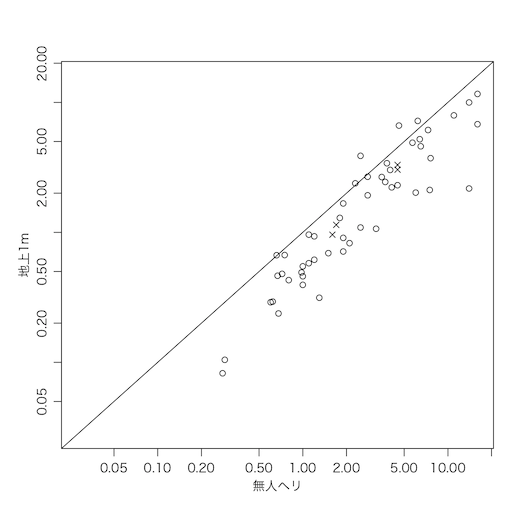
これも強いて地上/ヘリの累積分布をグラフにすれば次のようになる:
x = na.omit(rad/avi)
p = c(0.01,0.1,0.5,0.9,0.99)
q = c(0.15,0.2,0.5,1,1.5)
n = length(x)
plot(sort(x), qnorm((1:n)/n), type="s", xlab="ground/airborne", ylab="cumulative prob.",
log="x", xaxt="n", yaxt="n", xlim=c(0.15,1.5), ylim=qnorm(c(0.01,0.99)),
panel.first=abline(h=qnorm(p),v=q,col="lightgray"))
axis(2, qnorm(p), p)
axis(1, q, q)
m = median(x) # 0.659749
segments(m, -4, m, 0, col="lightgray")
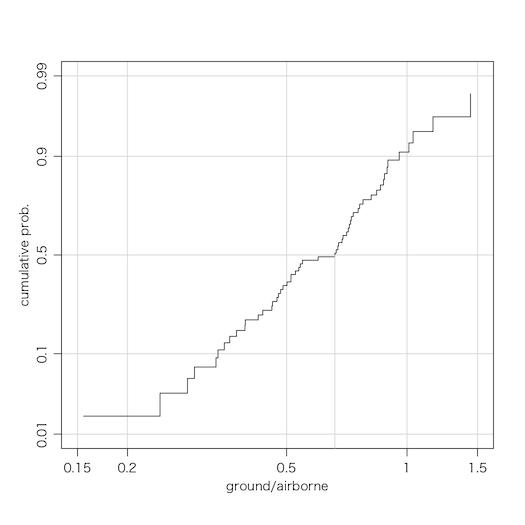
中央値は 0.66 ほどである。