Fraserのパラドックス（続）

Fraserのパラドックスの続編である。

とりあえずRでシミュレーションしてみよう。

与えられた事前分布に基づき，パラメータ $x$ を選ぶ。それに基づき，データ $y$ を生成する。そのデータから，常に $x_1 = \mathrm{max}(\lfloor y/2 \rfloor, 1)$ を選ぶ方法と，事後確率最大の $x$ を選ぶ方法を適用し，それぞれ正解なら 1，そうでないなら 0 を返す。これを多数回実行し，成績を比較する。

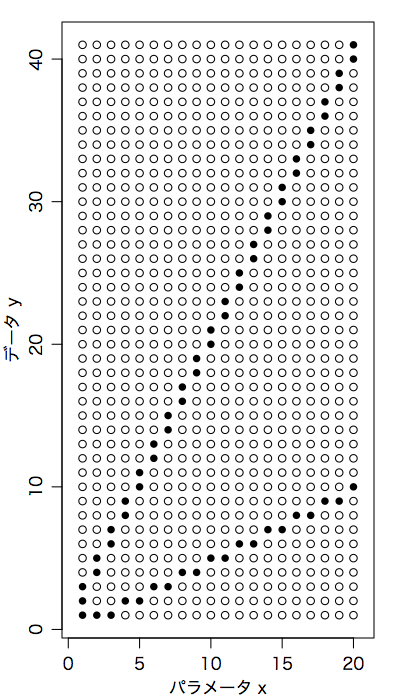
この時点で，前ページで挙げた正方形の尤度の表ではまずく，次のように $y$ のほうが長い表でないといけないことがわかるであろう。

この図からわかるように，$y$ のかなりの範囲で $x$ の推定値は一択である。

事前分布としては一様乱数を使ってみる。

nx = 20
ny = 2*nx+1
prior = runif(nx)  # 事前分布
lik = matrix(0, nrow=nx, ncol=ny)  # 尤度
for (x in 1:nx) {
    lik[x, max(floor(x/2), 1)] = 1/3
    lik[x, 2*x] = 1/3
    lik[x, 2*x+1] = 1/3
}
f = function() {  # シミュレーション
    x = sample(1:nx, 1, prob=prior)
    y = sample(1:ny, 1, prob=lik[x,1:ny])
    x1 = max(floor(y/2), 1)
    xbayes = which.max(prior * lik[1:nx,y])
    c(x1 == x, xbayes == x)
}
r = replicate(100000, f())  # 10万回
rowMeans(r)  # それぞれの方法の成績 mean(r[1,]), mean(r[2,])

実際にやってみるとわかるが，第1の方法は確かに少なくとも2/3の勝率である。しかし第2の方法はさらに勝率が良い。

つまり，事前分布がわかるなら，単純にベイズを適用するのがベストである。事前分布がまったくわからないなら第1の方法が良いが，このモデルについては，単調減少する事前分布を仮定して事後分布最大を選ぶことと同じである。