Fraserのパラドックス

D.A.S. Fraser, G. Monette and K.-W. Ng, "Marginalization, likelihood and structured models" (in P.R. Krishnaiah, ed., Multivariate Analysis -- VI, Elsevier (1985), 209--217) [PDF] に挙げられている例である。Yudi Pawitan, In All Likelihood で紹介されていた。ここではちょっと言い回しを変えてパラドックス風に提示する。

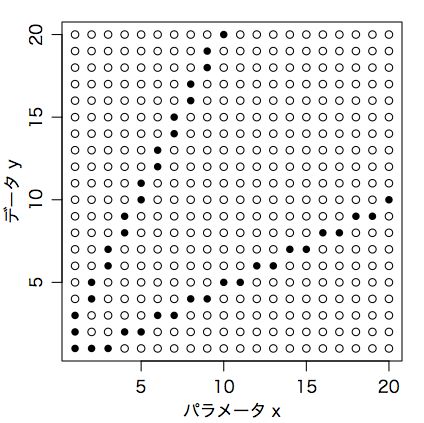
パラメータ $x = 1,2,3,\ldots$ によってデータ $y = 1,2,3,\ldots$ が次の図のように確率的に生じるモデルを考える。黒丸は確率 1/3，白丸は確率 0 である。

$x$ が与えられたときの $y$ の確率を $p(y \mid x)$ と書けば，$y = \mathrm{max}(\lfloor x/2 \rfloor, 1)$, $2x$, $2x+1$ のとき $p(y \mid x) = 1/3$ で，それ以外のとき $p(y \mid x) = 0$ である。

上の図はRで次のように描いた：

plot(NULL, xlim=c(1,20), ylim=c(1,20), xlab="パラメータ x", ylab="データ y")
for (x in 1:20) {
    points(rep(x,20), 1:20, pch=ifelse(1:20 %in% c(max(floor(x/2), 1), 2*x, 2*x+1), 16, 1))
}

モデルのパラメータ $x$ は直接は調べることができないが，データ $y$ から推測することができる。これが統計学の仕事である。この場合，データ $y$ が一つ与えられたならば，パラメータ $x$ には3通りの可能性 $x_1 = \mathrm{max}(\lfloor y/2 \rfloor, 1)$, $x_2 = 2y$, $x_3 = 2y+1$ がある。

次のように考えれば，3つの可能性のうち最も小さい値 $x_1$ を選ぶのが最も得策であることがわかる。

仮に真のパラメータの値が $x = 1$ であったとする。このとき，$y = 1$, $2$, $3$ がどれも確率 1/3 で生じる。このどの場合も $x_1 = 1$ である。したがって，$x_1$ を採用すればつねに正解 1 を得る。

また，仮に $x = 2$ であったとする。このとき，$y = 1$, $4$, $5$ がどれも確率 1/3 で生じる。このそれぞれの場合について，$x_1$ は 1, 2, 2 である。したがって，$x_1$ を採用すれば確率 2/3 で正解 2 を得る。これに対して，3つの可能性の中央値 $x_2$ を採用すれば，確率 1/3 で正解 2 を得る。3つの可能性の最大値 $x_3$ を採用すれば，正解に至らない。

また，仮に $x = 3$ であったとする。このとき，$y = 1$, $6$, $7$ がどれも確率 1/3 で生じる。このそれぞれの場合について，$x_1$ は 1, 3, 3 である。したがって，$x_1$ を採用すれば確率 2/3 で正解 3 を得る。これに対して，$x_2$ を採用すれば正解に至らない。$x_3$ を採用すれば確率 1/3 で正解 3 を得る。

同様に考えていけば，$x$ の真の値が何であっても，常に $x_1$ を採用すれば，少なくとも確率 2/3 で正解を得る。したがって，この方策がベストである。

を使って，事前分布 $p(x)$ と尤度 $p(y \mid x)$ から事後分布 $p(x \mid y)$ を求めるのがベイズ統計である。この場合，0でない3個の尤度はすべて等しい：

したがって，事後分布を最大にするためにどの可能性を採用すべきかは，事前分布 $p(x)$ だけによって決まる。$p(x_1)$, $p(x_2)$, $p(x_3)$ を比べて最も大きいものを選べばよい。

ところが，最初の考察によれば，事前分布によらず，必ず最小の可能性 $x_1$ を選ぶべきである。