
[追記] Pythonによる人口ピラミッドと男女比(2020年版)も書いた。
NHKの地価 沖縄が国内初の″リーマン″超えというニュースで,全国と沖縄の人口ピラミッドの比較がある。男女・年齢別人口はe-Statにある平成27年(2015年10月)国勢調査によるものである。NHKのページはすぐ消えるかもしれないので,念のため全国の図を以下に引用しておく:

この図を見て気づくのは,目盛(特に縦軸)がないことである。ところどころ出っ張ったり引っ込んだりしているが,何歳なのかわからない。どうやらExcelで描くと目盛が面倒らしい。
そこでRで描いてみよう。まずデータをe-Statからいただいてくる。どのような方法が楽なのかわからないが,ここでは統計名「平成27年国勢調査 人口等基本集計(男女・年齢・配偶関係,世帯の構成,住居の状態など)」(表番号00310)からe-Statのデータベース機能を使って全域・全国籍の男女・年齢で分けた人口を取得する。整形したものを pop2015.csv として置いておく。年齢階級「110」は110歳以上を意味し,さらに下の最後の年齢階級「NA」は「年齢「不詳」」を意味する。
pop2015 = read.csv("https://okumuralab.org/~okumura/stat/data/pop2015.csv")
「年齢「不詳」」は使わないので,削除する:
p = subset(pop2015, !is.na(Age))
Rで一番簡単に人口ピラミッドを描くには,すでにほかのいくつかのページでも使った中澤 港 先生の pyramid パッケージを使うのが便利である。ここではデフォルトの色(Lcol="Cyan", Rcol="Pink")ではないものを使ってみた:
install.packages("pyramid")
library(pyramid)
pyramids(p$Male, p$Female, p$Age, Cstep=10, Laxis=c(0,6e5,12e5), Lcol="#0080ff", Rcol="#ff8000")
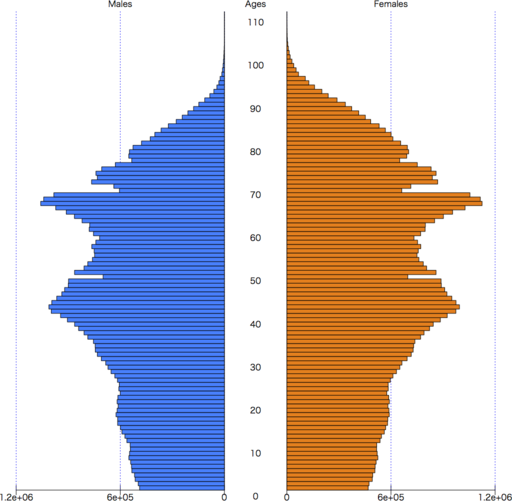
パッケージのお世話にならず直接描くには,例えば次のようにすればよい:
par(mar=c(1,1,1,10)) # 通常は(1,1,1,1)でいいが右余白に説明を書き込むため
m = max(p$Female, p$Male)
barplot(p$Female, space=0, horiz=TRUE, axes=FALSE, col="#ff8000", xlim=c(0,2.2*m), offset=1.2*m)
text(1.1*m, (0:10)*10, (0:10)*10, las=1, xpd=NA)
barplot(-p$Male, space=0, horiz=TRUE, axes=FALSE, col="#0080ff", add=TRUE, offset=m)
mtext("1973 第2次ベビーブーム", side=4, at=2015.5-1973, las=1)
mtext("1966 ひのえうま", side=4, at=2015.5-1966, las=1)
mtext("1949 第1次ベビーブーム", side=4, at=2015.5-1949, las=1)
mtext("1945 終戦", side=4, at=2015.5-1945, las=1)
mtext("1939 第2次世界大戦", side=4, at=2015.5-1939, las=1)
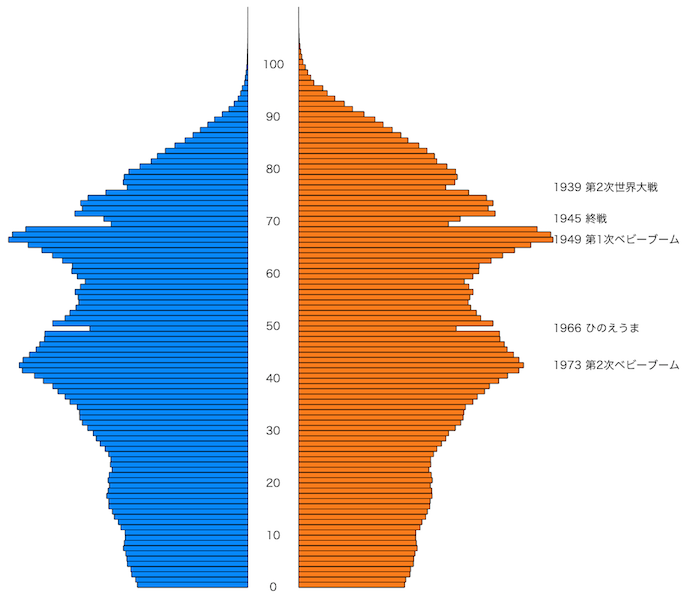
棒に境界線が不要なら,barplot() にオプション border=NA を加える。10歳刻みに薄い横線を引くには最初の barplot() にオプション panel.first=abline(h=(0:10)*10/length(p$Female), col="lightgray") を与える。
あるいは,ピラミッドにこだわらなければ,matplot() で簡単に描ける:
matplot(p[1], p[2:3], type="o", pch=16, xlab="Age", ylab="Population")
abline(v=49)
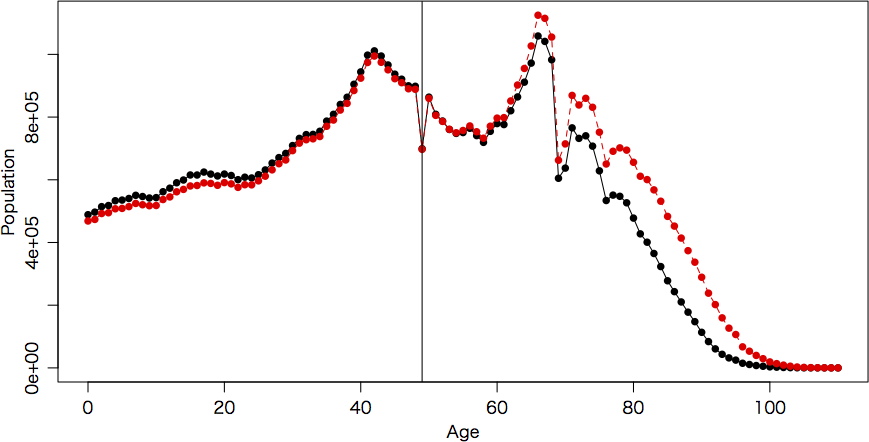
49歳のところに縦棒を引いた。どうしてここが引っ込んでいるかは,出生数と死亡数のところで述べた。
まったく別の話なのだが,一昨日(2017-09-20)ツイッターで話題になっていた「2児のうち一方が女ならもう一方も女である確率は?」という問題に関係して,男女比って1:1じゃないよねという話で,男のほうが5〜6%生まれやすい(出生性比参照)のだが,女に追いつかれるのは何歳かということにも疑問を持ったので,同じデータで調べてみよう。
plot(p$Age, p$Male/p$Female, type="o", pch=16, xlim=c(0,65), ylim=c(0.94,1.06),
xlab="Age", ylab="Male/Female", panel.first=grid(col="black")
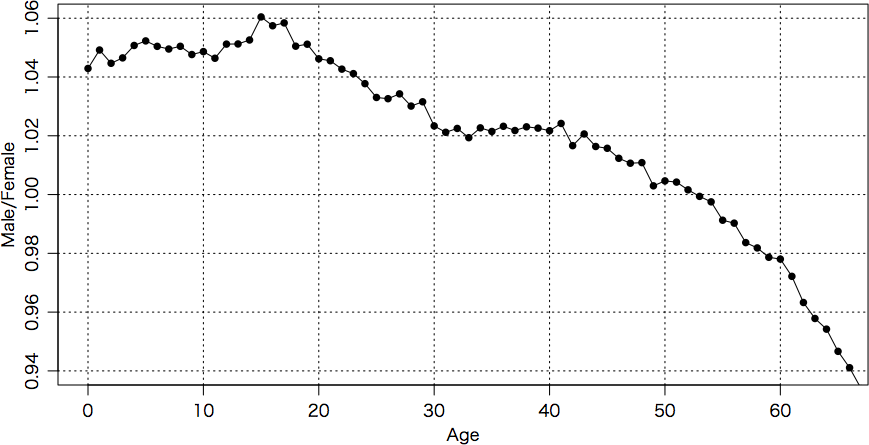
52〜53歳で追い抜かれることがわかる。