名古屋市のHPVVデータの解析

[おことわり] 以下はあくまでもRを使ったデータ解析法の例示で，HPVワクチンについて何らかの結論を主張するものではありません。

[2019-12-13追記] 自由記述の列229，275も含めたデータについては子宮頸がん予防接種調査の結果のPDFをCSV化をご覧ください。これ以外の列についてはすべて両者のデータが実質的に同一であることを確認しました。

データの読み込み

名古屋市のデータのCSV化でも書いたように，CSVに列275は含まれていない。また，列229は006001-024000の範囲がすべてNA（欠損値）になっている。これら自由記述欄以外の部分（半角数字の部分）は正しく変換されているはずである。

Nagoya-HPVV-data-01.zip を展開して kaito.csv を取り出して読む：

kaito = read.csv("kaito.csv", header=FALSE, colClasses="character", fileEncoding="UTF-8")
dim(kaito)
[1] 30793   274
head(kaito)
      V1 V2 V3 V4 V5 V6 V7 V8 V9 V10 V11 V12  V13 V14 V15 V16 V17 V18 V19  V20
1 000001  0  0  1  0  0  0  1  0   0   0   0 0000   0   0   0   0   0   2 0000
2 000002  0  1  0  0  0  0  0  0   1   0   1 0000   0   0   0   0   0   1 0000
3 000003  0  1  0  0  1  0  0  0   0   0   2 0000   2   0   1   0   0   1 0000
4 000004  0  0  1  0  0  0  0  0   0   1   1 0000   0   0   0   0   0   1 0000
5 000005  0  0  1  0  0  0  0  1   0   0   2 2610   1   1   0   0   0   2 2610
6 000006  1  0  0  0  1  0  0  0   0   0   1 0000   0   0   0   0   0   1 0000
……

同じことが data.table の fread() や readr の read_csv() でもできる：

library(data.table)
kaito_fread = fread("kaito.csv", header=FALSE, colClasses="character")
library(readr)
kaito_readr = read_csv("kaito.csv", col_names=FALSE, col_types=paste0(rep("c",274), collapse=""))

readr の read_csv() では変数名が X1，X2，… となることに注意する。

子宮頸がん予防接種（HPVV）の有無を表にしてみる：

table(kaito$V233)

    0     1     2     3 
  624  9245 20912    12

チェックなしが624人，なし9245人，あり20912人，両方チェックあり12人である。チェックなしや重複チェックは，他の項目の回答と照らし合わせて吟味するべきかもしれないが，ここでは単に無視する。

例：「身体が自分の意思に反して動く」

症状はいろいろある。ここではHPVV副作用としか考えられない症状（実際には思春期によく見られる）として「身体が自分の意思に反して動く」（V145）を例として調べる。なお，これはあくまでもデータ解析法の検討のための例示で，これだけから何らかの結論を導き出そうとしているわけではない。

table(kaito$V145)

    0     1     2 
  259 30272   262

チェックなし259人，なし30272人，あり262人である。これをHPVV有無とクロス集計すれば

table(kaito$V233, kaito$V145)

        0     1     2
  0    36   582     6
  1    80  9107    58
  2   143 20571   198
  3     0    12     0

つまり次のようになる：

	症状なし	症状あり
HPVVなし	9107	58
HPVVあり	20571	198

Fisherの正確検定をしてみる：

fisher.test(matrix(c(9107,20571,58,198),nrow=2))

	Fisher's Exact Test for Count Data

data:  matrix(c(9107, 20571, 58, 198), nrow = 2)
p-value = 0.005159
alternative hypothesis: true odds ratio is not equal to 1
95 percent confidence interval:
 1.121378 2.063976
sample estimates:
odds ratio 
  1.511313

非常に有意な関連がありそうである。しかし，他の変数と交絡しているかもしれないので，慎重に調べる必要がある。

まずは年齢が交絡しているかどうか調べる。まず年齢が必要である。この調査では列5〜11にそれぞれ平成6〜12年度生まれをチェックさせている。

table(rowSums(kaito[,5:11] == "1"))

    0     1     2 
  456 30334     3

チェックなしが456人，二つの年度にわたってチェックしているのが3人いる。これらを除いて年齢を調べる（もっとエレガントな方法があるだろうが，面倒なので…）：

birth = ifelse(rowSums(kaito[,5:11]=="1") != 1, NA,
  ifelse(kaito[,5]=="1", 6,
  ifelse(kaito[,6]=="1", 7,
  ifelse(kaito[,7]=="1", 8,
  ifelse(kaito[,8]=="1", 9,
  ifelse(kaito[,9]=="1", 10,
  ifelse(kaito[,10]=="1", 11,
  ifelse(kaito[,11]=="1", 12, NA))))))))

よりエレガントな方法を教えていただいた：

birth <- as.numeric(apply(kaito[ ,5:11], 1, paste, collapse=""))
birth <- match(birth, 10^(6:0)) + 5

さらに別解をいただいた：

birth = as.matrix(kaito[,5:11] == "1") %*% 6:12
birth = ifelse(birth < 6 | birth > 12, NA, birth)

これは次のようにしてもよさそう。

birth = (kaito[,5:11] == "1") %*% 6:12
birth = ifelse(birth %in% 6:12, birth, NA)

分布は次の通り：

table(birth, useNA="ifany")
birth
   6    7    8    9   10   11   12 <NA>
4102 4227 4235 4484 4501 4241 4544  459

生まれた年度とHPVV接種率には強い関係がある：

s = table(kaito$V233, birth)
s
   birth
       6    7    8    9   10   11   12
  0   56   64   90   72   96   90  126
  1  496  428  452  663 1260 2038 3761
  2 3549 3735 3690 3745 3143 2112  656
  3    1    0    3    4    2    1    1

グラフにしてみよう：

plot(6:12, s[3,]/(s[2,]+s[3,])*100, ylim=c(0,100), type="o",
     pch=16, xlab="生まれた年度（平成）", ylab="接種率（%）")

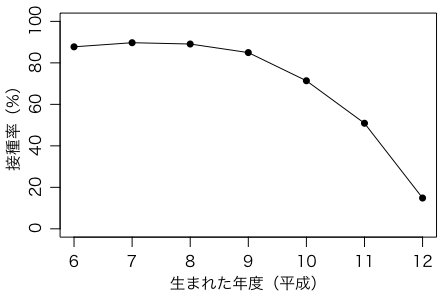
生まれた年度と「身体が自分の意思に反して動く」のクロス集計は次の通り：

u = table(kaito$V145, birth)
u
   birth
       6    7    8    9   10   11   12
  0   22   37   26   35   48   35   33
  1 4037 4141 4162 4414 4423 4176 4487
  2   43   49   47   35   30   30   24

グラフにしてみよう（95%信頼区間も付けた）：

plot(6:12, u[3,]/(u[2,]+u[3,])*100, ylim=c(0,2), type="o", pch=16,
     xlab="生まれた年度（平成）", ylab="症状の割合（%）")
ci = sapply(1:7, function(x)binom.test(u[3,x],u[2,x]+u[3,x])$conf.int)
arrows(6:12, 100*ci[1,], 6:12, 100*ci[2,], length=0.03, angle=90, code=3)

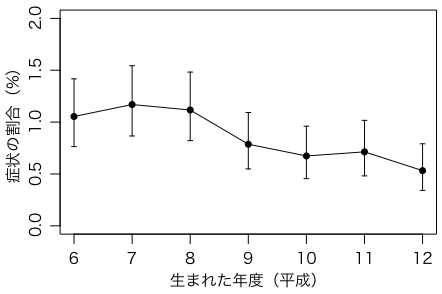
年齢が上（グラフで左側）のほうが少し多い傾向があるように見える。この傾向と，年齢が上のほうが接種率が高いこととが，年齢を交絡因子にしているのかもしれない。

横に生まれた年度（6〜12），縦に「症状なし・接種なし」「症状なし・接種あり」「症状あり・接種なし」「症状あり・接種あり」の度数を並べたクロス集計は次の通り：

t = sapply(1:7, function(x)as.numeric(table(kaito$V233, kaito$V145, birth)[2:3,2:3,x]))
t
     [,1] [,2] [,3] [,4] [,5] [,6] [,7]
[1,]  486  412  447  651 1232 2014 3722
[2,] 3496 3669 3627 3689 3097 2073  647
[3,]    6    9    1    6    8    9   18
[4,]   37   40   44   29   21   21    3

グラフにしてみよう（オレンジが接種あり，青が接種なし）：

# 接種なし
plot(6:12, t[3,]/(t[1,]+t[3,])*100, ylim=c(0,2.5), type="o",
     col="#0068b7", xlab="生まれた年度（平成）", ylab="症状の割合（%）")
ci = sapply(1:7, function(x)binom.test(t[3,x],t[1,x]+t[3,x])$conf.int)
arrows(6:12, 100*ci[1,], 6:12, 100*ci[2,], length=0.03, angle=90, code=3, col="#0068b7")
# 接種あり
points(6:12, t[4,]/(t[2,]+t[4,])*100, type="o", pch=16, col="#f39800")
ci = sapply(1:7, function(x)binom.test(t[4,x],t[2,x]+t[4,x])$conf.int)
arrows(6:12, 100*ci[1,], 6:12, 100*ci[2,], length=0.03, angle=90, code=3, col="#f39800")

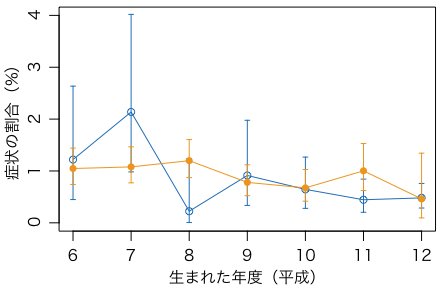
生まれた年度ごとに見ると，「身体が自分の意思に反して動く」症状が見られる割合は，接種群（オレンジ）も非接種群（青）もほぼ1%前後で生じている。両方併せれば，さきほど見たように，年齢が上（グラフで左側）のほうが少し多い傾向があるように見える。ただ，特に高年齢（左）側の非接種群（青）は人数が少ないので，変動が大きい。

メタアナリシスで解説したフォレストプロットを，生まれた年度ごとに描いてみよう：

library(metafor)
dat = escalc(measure="OR", ai=t[4,], bi=t[2,], ci=t[3,], di=t[1,])
res = rma(yi, vi, data=dat)
forest(res, slab=paste0("平成", 6:12, "年度生まれ"))

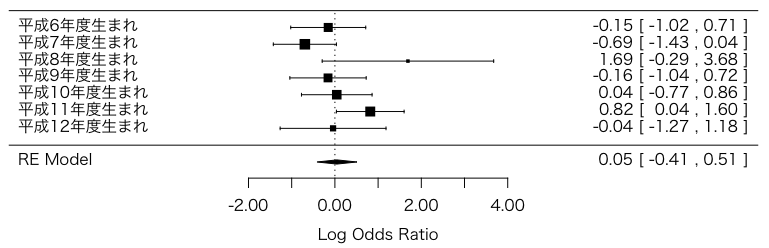
95%信頼区間を見ると，平成11年度生まれがかろうじて有意であるが，全体をまとめると対数オッズ比はほぼ 0（95%信頼区間 [-0.41, 0.51]）である。

なお，ここでのフォレストプロット（および一つ前のグラフ）の目的は，全体をまとめて一つの信頼区間で表し，それで何らかの結論を出すことではなく，個々の年齢層で違いがあるのかを吟味することである。例えば，接種率が8割を超えていた平成6〜9年度生まれと，急激に減少したそれ以降とで，傾向に違いがあるのか。

例：「なかなか眠れない」

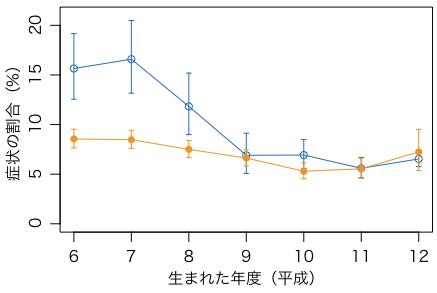
上の例は症例数が少ないのでサンプリング誤差も大きい。そこで，もうちょっと人数の多い（平凡な）症状を調べてみよう。V96（No.13）の「なかなか眠れない」である：

t = sapply(1:7, function(x)as.numeric(table(kaito$V233, kaito$V96, birth)[2:3,2:3,x]))
# 接種あり
plot(6:12, t[3,]/(t[1,]+t[3,])*100, ylim=c(0,21), type="o",
     col="#0068b7", xlab="生まれた年度（平成）", ylab="症状の割合（%）")
ci = sapply(1:7, function(x)binom.test(t[3,x],t[1,x]+t[3,x])$conf.int)
arrows(6:12, 100*ci[1,], 6:12, 100*ci[2,], length=0.03, angle=90, code=3, col="#0068b7")
# 接種あり
points(6:12, t[4,]/(t[2,]+t[4,])*100, type="o", pch=16, col="#f39800")
ci = sapply(1:7, function(x)binom.test(t[4,x],t[2,x]+t[4,x])$conf.int)
arrows(6:12, 100*ci[1,], 6:12, 100*ci[2,], length=0.03, angle=90, code=3, col="#f39800")
plot(6:12, t[3,]/(t[1,]+t[3,])*100, ylim=c(0,21), type="o",
     col="#0068b7", xlab="生まれた年度（平成）", ylab="症状の割合（%）")

library(metafor)
dat = escalc(measure="OR", ai=t[4,], bi=t[2,], ci=t[3,], di=t[1,])
res = rma(yi, vi, data=dat)
forest(res, slab=paste0("平成", 6:12, "年度生まれ"))

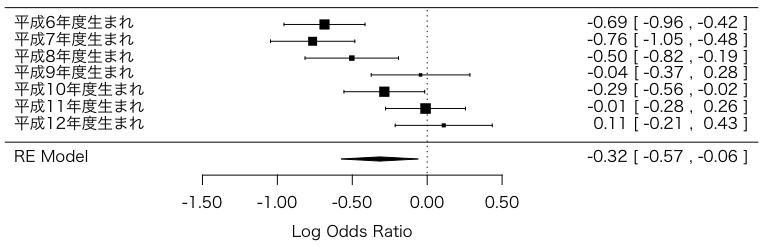
これはかなりはっきりした傾向がある。高年齢の非接種群はもともと睡眠障害があったのかもしれない（だから接種を見合わせたのかもしれない）。

（続きはそのうち書くかもしれない。）

リンク

tonkyo_Vcさんによる解析：tonkyo_Vcさんの2016-07-03のTwilog（下のTogetterに収録された）
Togetter: 名古屋市の子宮頸癌ワクチンアンケート調査データの解析に挑む
かるがもクリニック: HPVワクチンのお話４：名古屋市へのコメントなど