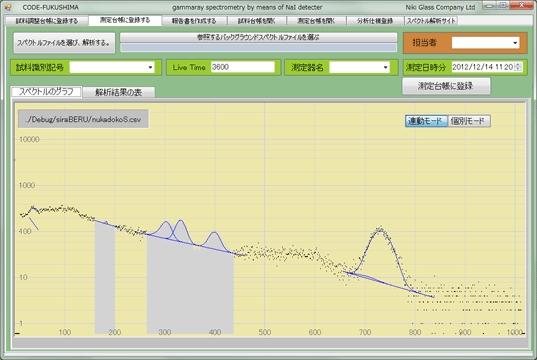
Code-Fukushima 開発者様から,以下の解析結果では「プログラムが正しく動作しておりません」というご指摘をいただきました。開発者様からご提供いただいた正しい画像は次のようになります(クリックすると大きくなります):
話の詳しい流れは 食品用の簡易放射線測定装置でできるだけよい測定を行うために:EMF211編 - Togetter 参照。
@suzuryo さんによる「糠どこ」測定例:
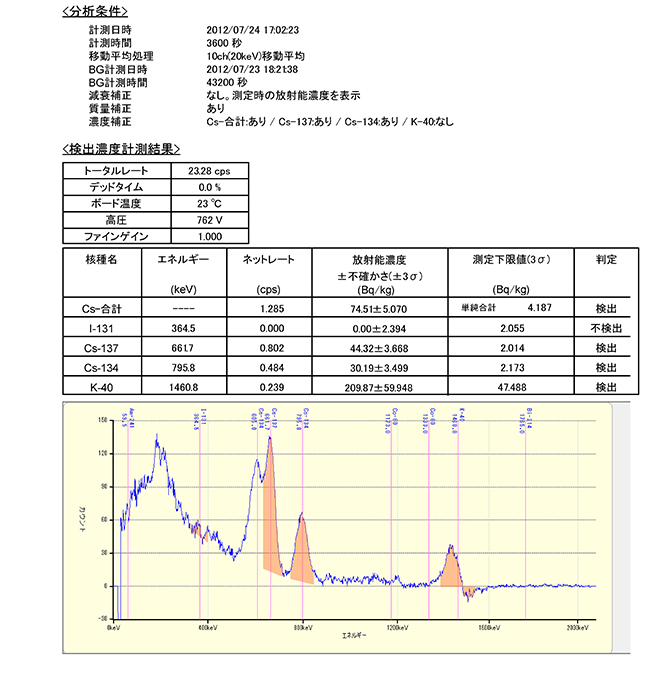
これを見ると,EMF211は,検体のスペクトルから,別に測定したバックグラウンドをスケールして差し引いて,その移動平均を積分していることがわかる。ただ,エネルギー(横軸)のゲインが変動するため,カリウムK-40のピークは明らかにおかしいことになっている。
EMF211の出力するテキストデータ(UTF-8,CRLF)
上記データをRやExcelで読み込めるようにしたCSVファイル nukadoko.csv(ASCII,CRLF)
上記を読み出すRコード:
data = read.csv("http://okumuralab.org/~okumura/stat/data/nukadoko.csv")
読めたか確認のため head(data, 15) として最初の15行程度を表示してみる(最初の10行は検体のスペクトルカウント sp,バックグラウンドカウント bg とも0)。
sp は3600秒,bg は43200秒のカウントである。合わせるために bg を3600/43200倍して重ねてプロット:
par(mgp=c(2,0.8,0)) # 余白の微調整
plot(data$ch, data$sp, type="l",
xlab="Channel", ylab="Counts", col="#f39800")
points(data$ch, data$bg*(3600/43200), type="l",
xlab="Channel", ylab="Counts", col="#0068b7")
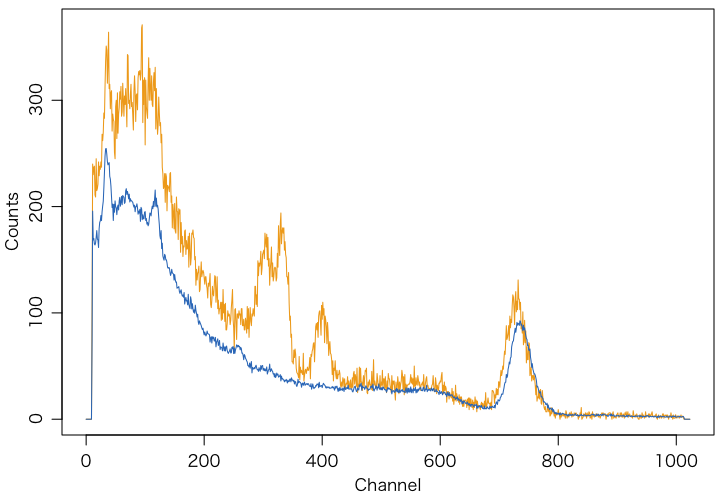
K-40は確かにずれている(ただしCs-134の1400keVのサムピークが重なっているかもしれない)。このようなデータでバックグラウンドを引いて使うのはまずい。そこで,バックグラウンドを引く前のスペクトルをピークフィットしてみる。511keVの電子のピークがバックグラウンドにも見えているので,これも含めてピークフィットする。
仮定としては,誤差モデルがPoissonであること(nlme
パッケージの gnls() を使う),チャンネルの範囲を200〜500(ほぼ400keV〜1MeV)に限ること,バックグラウンドは2次式で近似すること,ピークはCs-137(662keV),Cs-134(563・569・605・796・802keV),電子(511keV)を含めること(詳しいエネルギーと分岐比はおもな放射性核種参照),ピークの形状は正規分布(Gaussian)で,ピーク幅はピークの位置の平方根に比例し,NaIの効率曲線はエネルギーのベキ関数とした。ピーク位置は近いものはまとめた。
library(nlme)
r = 200:500
fit = gnls(sp ~ (c + d*(ch-350) + b*(ch-350)^2 +
(e1*(0.08338/0.9226)*dnorm((ch-0.9314*m1)/(0.9226*s)) +
e1*(0.15373/0.9276)*dnorm((ch-0.9415*m1)/(0.9276*s)) +
e1*(0.9762/0.956)*dnorm((ch-m1)/(0.956*s)) +
e2*0.851*dnorm((ch-m2)/s) +
e1*(0.8546/1.0967)*dnorm((ch-m3)/(1.0967*s)) +
e1*(0.08688/1.101)*dnorm((ch-1.00765*m3)/(1.101*s)) +
e4*dnorm((ch-m4)/(0.8788*s))
) / s
) * (ch/350)^u,
data=data, subset=r,
start=list(c=20,d=-1,b=0.02,e1=1000,e2=1000,
m1=300,m2=340,m3=400,
e4=200,m4=255,
s=5,u=-1.2),
weights=varPower(fixed=0.5),
control=list(nlsTol=1e-4)) # 収束しないときは1e-3に直す
plot(data$ch, data$sp, type="l",
xlab="Channel", ylab="Counts", xlim=range(r), col="#f39800")
points(data$ch[r], fitted(fit), type="l")
a = coef(fit)
points(data$ch[r], type="l",
(a['c']+a['d']*(data$ch[r]-350)+a['b']*(data$ch[r]-350)^2)
* (data$ch[r]/350)^a['u'])
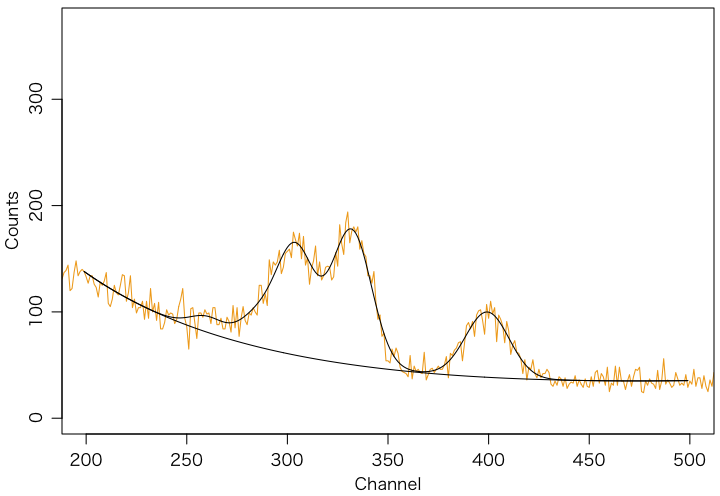
summary(fit) の結果の一部を抜き書きする:
Coefficients:
Value Std.Error t-value p-value
c 46.043 1.51420 30.4075 0.000
d -0.061 0.03726 -1.6310 0.104
b 0.001 0.00015 4.9744 0.000
e1 2065.207 73.51652 28.0917 0.000
e2 3449.141 129.24325 26.6872 0.000
m1 304.292 0.52335 581.4279 0.000
m2 332.221 0.36674 905.8817 0.000
m3 399.441 0.49236 811.2740 0.000
e4 253.608 56.15714 4.5160 0.000
m4 260.532 2.22883 116.8920 0.000
s 9.845 0.27185 36.2133 0.000
u -1.154 0.20240 -5.6994 0.000
つまり,e1 つまりCs-134の係数は誤差の28倍で,e2
つまりCs-137の係数は誤差の27倍である。
Cs-137の具体的な値を得るには,
sum(a['e2']*0.851*dnorm((data$ch[r]-a['m2'])/a['s'])/a['s']*(data$ch[r]/350)^a['u'])
と打ち込めば 3120.564 が出るが,これを3600秒で割ってcps値に直し,EMF211出力のテキストファイルにある「Cs-137換算係数=68.1」を掛けて,「質量=573.5」で割れば,102.9Bq/kg になる。誤差σは e2 の t-value で割って 3.86Bq/kg である。このページの一番上の図にある 44.32±3.668 Bq/kg とかなり違う。
Cs-134のほうはテキストファイルに「Cs-134換算係数=75.6」と書き込まれているが,これは796keVのピークについての値であり,ここではCs-137の a['e1']/a['e2'] 倍すなわち 0.5987599 倍として計算するほうがよい(事故時 1:1 として今ごろはこんな値である)。すると,61.6Bq/kg で,誤差は 2.19Bq/kg となる。
Last modified: 2012-12-14 13:41:19