ベルトールドのLB2045はNaIを使ったガンマ線スペクトルメータである。
本体だけで計測することも,PCを接続して専用ソフトJ-Gammaで計測することもできる。理由は不明だが,両者でcalibration factorが異なる。本体用の値として,ファームウェアバージョン2.20未満では35程度,2.20以上では83程度の値が校正シートに書かれているが,いずれも 137Cs について,前者はBq/cps,後者はBq/L/cps単位のようである(マリネリ容器の容量0.42Lだけ異なる)。J-Gamma用のcalibration factorは固定である。詳細は不明だが,効率を660keVでは0.025,800keVでは0.019,600keVでは0.027としているようである。660keVで効率0.025ということは,137Cs のcalibration factorが 1/0.85/0.025 = 47 に相当する。不可解な仕様だが,ベルトールドジャパンではこれを説明できないらしい。
まず十分ウォーミングアップしてから付属の9kBqの 137Cs 線源でエネルギー校正する。これはすぐ完了し,本体での表示は662keVにぴったり合うように見える。しかし,この状態でRS232C経由でPCにデータを送って,PC側のソフトJ-Gammaで表示すると,かなりずれている。この不具合はベルトールドジャパンでも認識していて,修正される予定とのことである(といいながらちっとも修正されない)。
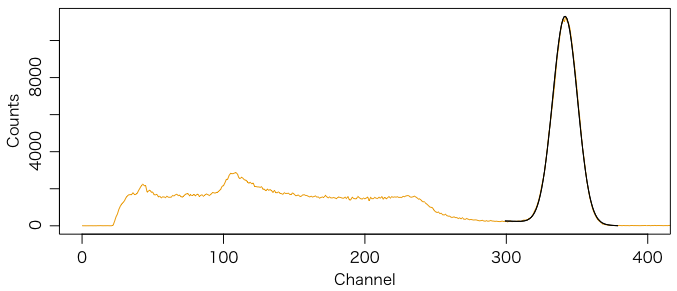
J-Gammaを使わなくても,PCに取り込まれた結果のテキストファイルをRでフィットすればよい。付属の9kBqの 137Cs 線源を測定した結果が 120615155505.TXT である。このデータ部分を取り出してプロットすると,次のオレンジ色のグラフが得られる(黒部分は後述):

662keVのピークがきれいに見える。この半分のエネルギーを対称の中心として二つ見える崖はCompton edge(コンプトン端(たん))と後方散乱ピークである。正確なピーク位置はおもな放射性核種参照。次の計算で「511」と書いた値は電子質量(keV単位)である(Particle Data Groupの最新の値は 0.510998928 ± 0.000000011 MeV)。
1/(2/511+1/661.657) # 184.3233 後方散乱
661.657-1/(2/511+1/661.657) # 477.3337 Compton
上のグラフを描くには次のようにする:
sp = scan("http://okumuralab.org/~okumura/stat/data/120615155505.TXT",
skip=39, nlines=1024, comment.char=";") # スペクトルを読む
sp = floor(sp * 601 + 0.5) # cpsからカウント(整数)に変換。601は秒数
ch = 0:1023 # チャンネル番号
par(mgp=c(2,0.8,0)) # Rのグラフィックオプションを好みでいじる
plot(ch, sp, type="l", xlab="Channel", ylab="Counts", xlim=c(0,400), col="#f39800")
横軸はチャンネル番号(0〜1023)のままにした。400以上は特にフィーチャーがないので省略した。
まずはコベル法でピークカウントを積分してみる。出力はコメント(#
で始まる行)で示す。
sum(sp[301:379]) - 79 * mean(sp[c(280:300, 380:400)])
# [1] 244608
sum(sp[311:369]) - 59 * mean(sp[c(280:310, 370:400)])
# [1] 244520.4
1次式+正規分布でフィットしてみる。
# nlmeパッケージをインストールしていない場合:
# options(repos="http://cran.ism.ac.jp") # 例えば
# update.packages()
# install.packages("nlme")
library(nlme)
data = data.frame(ch=ch, sp=sp)
r = 300:380
fit = gnls(sp ~ c + d*(ch-340) + e*dnorm((ch-m)/s),
data=data, subset=r,
start=list(c=100,d=-3,e=30000,m=341,s=10),
weights=varPower(fixed=0.5),
control=list(nlsTol=1e-4))
points(ch[r], fitted(fit), type="l")
a = coef(fit)
a
# c d e m s
# 129.183659 -3.278402 28038.778015 341.573936 8.731706
sum(a['e']*dnorm((ch-a['m'])/a['s']))
# [1] 244826.4
どの方法で計算しても,ピーク面積は244500〜244800カウント程度である。最後のピークフィットの値を使うと,ピークの中心チャンネル a['m'] は 341.57 で,cps(counts per second)値は 244826.4 / 601 = 407.365 である。
ここで上の 120615155505.TXT の中を読めばわかるように,本体ではcps値を 504.8 と認識している。ROI(region of interest)すなわち積分範囲が広すぎるのかもしれない。
このcps値に calibration factor を掛けたものが 137Cs のBq値である。ここで,LB2045のファームウェアのバージョンが2.20より古いものは calibration factor として35程度の値を持っているが,この単位は Bq/cps である。より新しいものでは calibration factor が83程度であるが,この単位は Bq/L/cps で,LB2045のマリネリ容器の容量 0.42L で割った値になっている。
本機の場合,calibration factor が 83.0 であり,重量として(わざと変な値)4kg を設定したので,本体の 504.8cps を使って計算すると,
> 504.8 * 83 * 0.42 / 4
[1] 4399.332
となるべきであるが,本体表示値は 4397Bq/kg である。ほぼ一致していると見てよかろう(微妙な違いが出る理由は不明)。一方,上のフィット値を使えば
> 407.365 * 83 * 0.42 / 4
[1] 3550.186
となり,やや小さい。
この時点で,LB2045の 137Cs の662keVでの効率は0.025程度であるという裏情報を得た。137Cs の1Bqは1秒間に0.851個の662keVガンマ線を放出するので,これは 1 / 0.851 / 0.025 = 47 (Bq/cps) に相当する。この値を使えば,
> 407.365 * 47 / 4
[1] 4786.539
となり,今度は少し大きめに出る。
以上をまとめると,Cs-137 の calibration factor は 34Bq/cps ないし 47Bq/cps 程度である。
成功した解析は下にあるが,失敗例も載せておく。
データは 120615162546.TXT である。
sp = scan("http://okumuralab.org/~okumura/stat/data/120615162546.TXT",
skip=39, nlines=1024, comment.char=";")
sp = floor(sp * 600 + 0.5)
data = data.frame(ch=ch, sp=sp)
単純に2次式+三山でフィット。
fit = gnls(sp ~ c + d*(ch-350) + b*(ch-350)^2
+ e1*dnorm((ch-m1)/s1)
+ e2*dnorm((ch-m2)/s2)
+ e3*dnorm((ch-m3)/s3),
data=data, subset=250:450,
start=list(c=200,d=-5,b=0.01,e1=10000,e2=10000,e3=10000,
m1=300,m2=340,m3=400,s1=10,s2=10,s3=10),
weights=varPower(fixed=0.5),
control=list(nlsTol=1e-4)) # 収束しないときは1e-3に直す
a = coef(fit)
a
# c d b e1 e2
# 2.112697e+02 -4.976858e+00 3.468806e-02 9.032938e+03 1.008448e+04
# e3 m1 m2 m3 s1
# 6.078507e+03 3.124179e+02 3.430158e+02 4.070545e+02 1.340072e+01
# s2 s3
# 7.821025e+00 1.015221e+01
plot(ch, sp, type="l", xlab="Channel", ylab="Counts", xlim=c(0,500), col="#f39800")
points(data$ch[250:450], fitted(fit), type="l")
points(data$ch[250:450], type="l",
a['c']+a['d']*(data$ch[250:450]-350)+a['b']*(data$ch[250:450]-350)^2)
sum(a['e1']*dnorm((data$ch-a['m1'])/a['s1']))
# [1] 121047.8
sum(a['e2']*dnorm((data$ch-a['m2'])/a['s2']))
# [1] 78870.94
sum(a['e3']*dnorm((data$ch-a['m3'])/a['s3']))
# [1] 61710.29
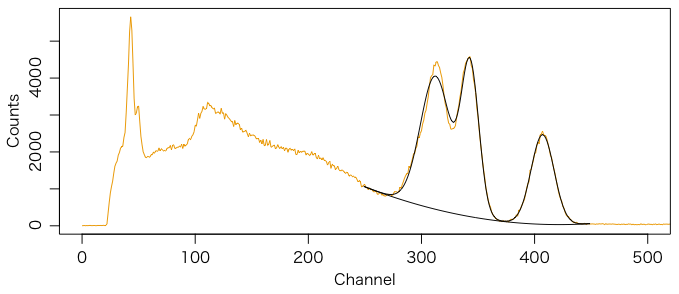
あまり合わない。
データは 120615162546.TXT である。
sp = scan("http://okumuralab.org/~okumura/stat/data/120615162546.TXT",
skip=39, nlines=1024, comment.char=";")
sp = floor(sp * 600 + 0.5)
ch = 0:1023
par(mgp=c(2,0.8,0))
plot(ch, sp, type="l", xlab="Channel", ylab="Counts", xlim=c(0,500), col="#f39800")
マイナーなピークも入れる(より正確な値はおもな放射性核種参照)。
| Cs-134 | Cs-137 | ||||
|---|---|---|---|---|---|
| 563keV | 569keV | 605keV | 796keV | 802keV | 662keV |
| 8.4% | 15.4% | 97.6% | 85.5% | 8.7% | 85.1% |
ただし,パラメータが多くなりすぎないように,適宜まとめる。ピーク幅はエネルギーの平方根に比例すると仮定,効率曲線はベキ乗則に従うとした。また,和田先生のご指摘により,ピークの係数を s で割った形にした。
r = 260:450
data = data.frame(ch=ch, sp=sp)
fit = gnls(sp ~ (c + d*(ch-350) + b*(ch-350)^2
+ (e1*(0.08338/0.9226)*dnorm((ch-0.9314*m1)/(0.9226*s)) +
e1*(0.15373/0.9276)*dnorm((ch-0.9415*m1)/(0.9276*s)) +
e1*(0.9762/0.956)*dnorm((ch-m1)/(0.956*s)) +
e2*0.851*dnorm((ch-m2)/s) +
e1*(0.8546/1.0967)*dnorm((ch-m3)/(1.0967*s)) +
e1*(0.08688/1.101)*dnorm((ch-1.00765*m3)/(1.101*s))) / s)
* (ch/350)^u,
data=data, subset=r,
start=list(c=200,d=-3,b=0.02, # 初期値
e1=10000,e2=10000, # 収束しないときは適宜直す
m1=313,m2=342,m3=407,s=9,u=-1.2),
weights=varPower(fixed=0.5),
control=list(nlsTol=1e-4)) # 収束しないときは1e-3に直す
a = coef(fit)
plot(ch, sp, type="l", xlab="Channel", ylab="Counts", xlim=c(0,500), col="#f39800")
points(ch[r], fitted(fit), type="l")
points(ch[r], type="l",
(a['c']+a['d']*(ch[r]-350)+a['b']*(ch[r]-350)^2)
* (ch[r]/350)^a['u'])
a
# c d b e1 e2
# 1.726192e+02 -3.278716e+00 2.336625e-02 7.757909e+04 1.103418e+05
# m1 m2 m3 s u
# 3.134416e+02 3.415751e+02 4.069815e+02 9.027592e+00 -1.188280e+00
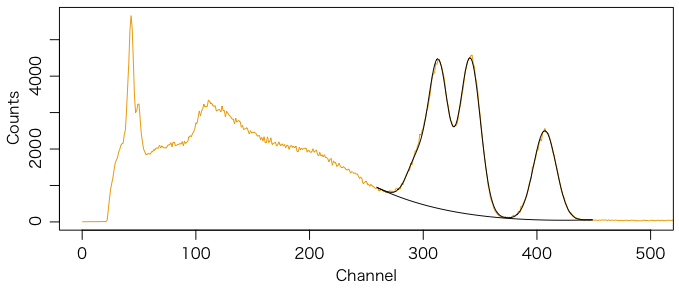
図はよく合う。
効率曲線はエネルギーの -1.2 乗くらいということになる。137Cs の量は,カウントを600秒で割ってcpsに直して calibration factor を掛けて
sum(a['e2']*0.851*dnorm((ch[r]-a['m2'])/a['s'])/a['s']*(ch[r]/350)^a['u']) / 600 * 83 * 0.42
# [1] 5621.019
sum(a['e2']*0.851*dnorm((ch[r]-a['m2'])/a['s'])/a['s']*(ch[r]/350)^a['u']) / 600 * (1/0.851/0.025)
# [1] 7579.108
つまり 5621Bq ないし 7579Bq である。134Cs と 137Cs の比は
a['e1']/a['e2']
で 0.7030798 となり,Cs-137校正のベクレルメータの補正でも計算できるように,2012-06-15(大量放出から1.25年)の値として妥当である。
フィッティングの詳細は
summary(fit)
で調べる。関係のある出力を書き出しておく:
Coefficients:
Value Std.Error t-value p-value
c 172.62 5.4547 31.646 0
d -3.28 0.0669 -48.996 0
b 0.02 0.0009 25.938 0
e1 77579.09 359.9130 215.550 0
e2 110341.80 664.3885 166.080 0
m1 313.44 0.0799 3923.023 0
m2 341.58 0.0615 5557.321 0
m3 406.98 0.0672 6056.817 0
s 9.03 0.0361 250.060 0
u -1.19 0.0336 -35.325 0
Correlation:
c d b e1 e2 m1 m2 m3 s
d -0.072
b -0.684 -0.512
e1 -0.484 0.030 0.263
e2 -0.392 -0.089 0.321 0.124
m1 0.083 0.012 -0.019 0.049 -0.323
m2 -0.184 0.105 0.086 0.205 -0.156 0.399
m3 0.234 0.042 -0.270 -0.083 -0.110 0.031 -0.020
s -0.540 -0.085 0.346 0.306 0.321 -0.216 -0.024 -0.099
u 0.042 -0.748 0.402 0.028 0.206 -0.240 -0.252 -0.088 0.121
各パラメータの相対誤差は t-value の逆数(Std.Error / Value)である。u
を固定値と考えれば,134Cs と 137Cs の誤差はほぼ
e1 と e2 の誤差と考えてよい。両者の和の誤差は,
v = vcov(fit)
sqrt(v['e1','e1'] + 2*v['e1','e2'] + v['e2','e2'])
で 793.7626 となる(e1 と e2 の誤差の和 1024.302 より小さいのは両者に正の相関があるからである)。
データは 120704151211.TXT である。これは上の例に比べて汚染も少ないので効率曲線はエネルギーの -1.2 乗に固定して計算した。
sp = scan("http://okumuralab.org/~okumura/stat/data/120704151211.TXT",
skip=38, nlines=1024, comment.char=";")
sp = floor(sp * 601 + 0.5)
data = data.frame(ch=ch, sp=sp)
r = 260:450
fit = gnls(sp ~ (c + d*(ch-350) + b*(ch-350)^2
+ (e1*(0.08338/0.9226)*dnorm((ch-0.9314*m1)/(0.9226*s)) +
e1*(0.15373/0.9276)*dnorm((ch-0.9415*m1)/(0.9276*s)) +
e1*(0.9762/0.956)*dnorm((ch-m1)/(0.956*s)) +
e2*0.851*dnorm((ch-m2)/s) +
e1*(0.8546/1.0967)*dnorm((ch-m3)/(1.0967*s)) +
e1*(0.08688/1.101)*dnorm((ch-1.00765*m3)/(1.101*s))) / s)
* (ch/350)^(-1.2),
data=data, subset=r,
start=list(c=200,d=-3,b=0.02,e1=10000,e2=10000,
m1=313,m2=342,m3=407,s=9),
weights=varPower(fixed=0.5),
control=list(nlsTol=1e-4)) # 収束しないときは1e-3に直す
a = coef(fit)
plot(ch, sp, type="l", xlab="Channel", ylab="Counts", xlim=c(0,500), col="#f39800")
points(ch[r], fitted(fit), type="l")
points(ch[r], type="l",
(a['c']+a['d']*(ch[r]-350)+a['b']*(ch[r]-350)^2)
* (ch[r]/350)^(-1.2))
summary(fit)
# Coefficients:
# Value Std.Error t-value p-value
# c 8.4041 0.73743 11.3965 0.0000
# d -0.0626 0.00514 -12.1765 0.0000
# b 0.0004 0.00012 3.1630 0.0018
# e1 1185.0545 35.78182 33.1189 0.0000
# e2 1819.2397 64.36106 28.2662 0.0000
# m1 316.7075 0.46358 683.1753 0.0000
# m2 343.3805 0.33962 1011.0819 0.0000
# m3 409.2899 0.42369 966.0059 0.0000
# s 8.7932 0.22063 39.8554 0.0000
sum(a['e2']*0.851*dnorm((ch[r]-a['m2'])/a['s'])/a['s']*(ch[r]/350)^(-1.2)) / 600 * 83 * 0.42
# [1] 92.11347
sum(a['e2']*0.851*dnorm((ch[r]-a['m2'])/a['s'])/a['s']*(ch[r]/350)^(-1.2)) / 600 * (1/0.851/0.025)
# [1] 124.2013
a['e1']/a['e2']
# 0.651401
v = vcov(fit)
sqrt(v['e1','e1'] + 2*v['e1','e2'] + v['e2','e2'])
# [1] 80.55856
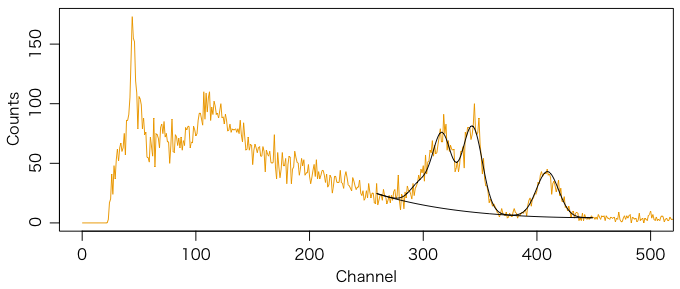
上の計算のように 137Cs は 92Bq ないし 124Bq である(サンプルの重量 0.432kg
で割れば Bq/kg 単位になる)。相対誤差(1σ)は e2
の t-value の逆数で3.5%ほど。
みかげさんのSPViewerのLB2045サンプル(白米)を使った例。43201秒(半日)計測。これはよく見ないと山が見えないほどのもの。しかも511にも山がある。
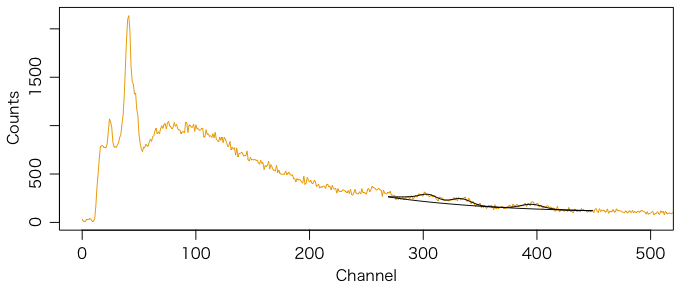
上と同じようにできるが,511の山を回避するため,下限を少し上にした。
sp = scan("http://www.mikage.to/radiation/spviewer/lb2045_120122220029.txt",
skip=35, nlines=1024, comment.char=";")
sp = floor(43201 * sp + 0.5)
data = data.frame(ch=ch, sp=sp)
r = 270:450
fit = gnls(sp ~ (c + d*(ch-350) + b*(ch-350)^2
+ (e1*(0.08338/0.9226)*dnorm((ch-0.9314*m1)/(0.9226*s)) +
e1*(0.15373/0.9276)*dnorm((ch-0.9415*m1)/(0.9276*s)) +
e1*(0.9762/0.956)*dnorm((ch-m1)/(0.956*s)) +
e2*0.851*dnorm((ch-m2)/s) +
e1*(0.8546/1.0967)*dnorm((ch-m3)/(1.0967*s)) +
e1*(0.08688/1.101)*dnorm((ch-1.00765*m3)/(1.101*s))) / s)
* (ch/350)^(-1.2),
data=data, subset=r,
start=list(c=200,d=-3,b=0.02,e1=10000,e2=10000,
m1=313,m2=342,m3=407,s=9),
weights=varPower(fixed=0.5),
control=list(nlsTol=1e-4)) # 収束しないときは1e-3に直す
a = coef(fit)
plot(ch, sp, type="l", xlab="Channel", ylab="Counts", xlim=c(0,500), col="#f39800")
points(ch[r], fitted(fit), type="l")
points(ch[r], type="l",
(a['c']+a['d']*(ch[r]-350)+a['b']*(ch[r]-350)^2)
* (ch[r]/350)^(-1.2))
summary(fit)
# Coefficients:
# Value Std.Error t-value p-value
# c 167.4171 3.66841 45.6374 0.0000
# d -0.1892 0.02699 -7.0107 0.0000
# b 0.0015 0.00060 2.4351 0.0159
# e1 1421.5306 137.08970 10.3693 0.0000
# e2 1589.7410 192.99491 8.2372 0.0000
# m1 304.6055 0.97338 312.9351 0.0000
# m2 333.3311 0.97054 343.4482 0.0000
# m3 395.4143 1.08879 363.1687 0.0000
# s 8.9602 0.63998 14.0008 0.0000
sum(a['e2']*0.851*dnorm((ch[r]-a['m2'])/a['s'])/a['s']*(ch[r]/350)^(-1.2)) / 43201 * 83 * 0.42
# [1] 1.158605
sum(a['e2']*0.851*dnorm((ch[r]-a['m2'])/a['s'])/a['s']*(ch[r]/350)^(-1.2)) / 43201 * (1/0.851/0.025)
# [1] 1.562206
a['e1']/a['e2']
# 0.89419
v = vcov(fit)
sqrt(v['e1','e1'] + 2*v['e1','e2'] + v['e2','e2'])
# [1] 303.4506
つまり 137Cs は 1.15Bq ないし 1.56Bq,重量 0.3123kg で割れば 3.7Bq/kg ないし 5.0Bq/kg,その1σ相対誤差は e2 の t-value の逆数で約12%,つまり 0.45Bq/kg ないし 0.61Bq/kg である。134Cs / 137Cs 比は 0.89419,したがってCs合計は 137Cs の 1.89419 倍で,その1σ相対誤差は 303.4506 / (1421.5306 + 1589.7410) で約10%,つまり 0.71Bq/kg ないし 0.95Bq/kg である。
結論として,半日測れば誤差を 1Bq/kg 以下にできる。誤差の3倍を検出限界とすれば,3Bq/kg くらいは測れる。
Last modified: 2012-08-15 21:30:30