Mandelbrot集合

Python では複素数の演算が簡単にできます。例えば複素数 $3 + 4i$ は Python では 3 + 4j と書きます。虚数単位を $i$ ではなく $j$ とするのは工学系の慣習です。

z = 3 + 4j
abs(z)

5.0

さて、複素数 $c$ が与えられたとき、$z_0 = 0$ から初めて $z_{k+1} = z_k^2 - c$ という漸化式を適用してできる数列で $\{|z_k|\}$ が有界のときの $c$ の集合を Mandelbrot（マンデルブロー、マンデルブロート）集合といいます（$c$ の前の符号は $+$ でも $-$ でもかまいません）。この集合はフラクタルの例として知られています。

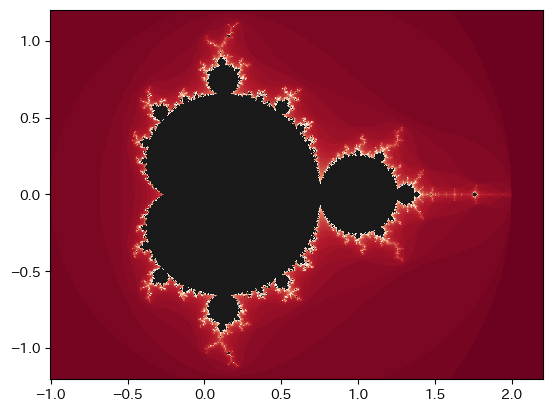
これを Python で描いてみましょう。結果をうまく表すため、$M$ を十分大きい整数として、$z_k \geq 2$ になる最小の $k \leq M$ によって $c$ の領域を色分けすることにします。

import matplotlib.pyplot as plt
import numpy as np

M = 100

def mandel(c):
    k = 0
    z = 0
    while k < M and abs(z) < 2:
        z = z ** 2 - c
        k += 1
    return k

vmandel = np.vectorize(mandel)

x, y = np.meshgrid(np.linspace(-1, 2.2, 640), np.linspace(-1.2, 1.2, 480))
z = vmandel(x + y * 1j)

plt.pcolormesh(x, y, z, cmap='RdGy', vmin=0, vmax=M)
plt.axis('scaled')
plt.show()
Mandelbrot set

この黒い部分が本来の Mandelbrot 集合です。

cmap='RdGy' の部分を Choosing Colormaps in Matplotlib を参照にして変えれば（あるいは Creating Colormaps in Matplotlib を参考にして新しいカラーマップを定義すれば）、色が変わります。

これで十分高速に実行できると思いますが、さらに高速にするために、Numba を使ってみましょう。変更部分は

from numba import jit

@jit(nopython=True)
def mandel(c):
    (以下同じ)

だけです。数倍速くなると思います。

たまたま Numba の対応する NumPy のバージョンより新しい NumPy をインストールしてしまったので from numba import jit でエラーになりました。この場合は pip install --upgrade numba を再実行すれば、NumPy のバージョンを落としてくれました。

「有界」というところをもうちょっと説明しておきます。

例えば $c = 0.5 + 0.5i$ のとき、数列 $\{z_i\}$ を複素平面でプロットしてみると、次のようになります。

import matplotlib.pyplot as plt

def mandel(c):
    z = 0
    x = [0]
    y = [0]
    for i in range(100):
        z = z ** 2 - c
        if abs(z) > 100:
            break
        x.append(z.real)
        y.append(z.imag)
    plt.clf()
    plt.plot(x, y, "o-")
    plt.axis('equal')

mandel(0.5 + 0.5j)
Mandelbrot sequence, an example

ある点に収束していくようで、$\{|z_k|\}$ は有界です。ところが

mandel(0.52 + 0.52j)

では急速に発散します。この境目が Mandelbrot 集合の境界です。

Last modified: