ABO血液型

はじめに

とあるツイッターでの血液型アンケートでは，297400票中，A 102229，O 89326，B 67376，AB 38469 という結果であった。割合では，A 34.4%，O 30.0%，B 22.7%，AB 12.9% である。

より小規模なこちらのアンケートでは，A 297，B 197，O 253，AB 123という結果であった。割合では，A 34.1%，B 22.6%，O 29.1%，AB 14.1% である。

[追記] 深田えいみさんのアンケートでは，537356票中，O型167791，A型186333，B型116163，AB型67069であった。

こういった結果は，母集団全体の比率と有意に異ならないか。もし異なるなら，何が原因だろう？

そもそも母集団の比率が正確にわからなければならない。信頼のおけるデータはないか。ということで，下の古畑（田中）のデータと，より新しい高校生2.1万人のデータを吟味することにした。

古畑（田中）のデータ

古畑種基『血液型の話』（岩波新書467，1962年）に当時の県別血液型分布の表が載っている（202〜205ページ）。「田中が集計した日本人一一四万八六二三名」（196ページ）とあるだけで出典はよくわからない。余談だが，ウィキペディア「古畑種基」によれば，古畑は四大死刑冤罪事件のうち3件に関わっている。冤罪を作り出した責任の一端を負うべき人物かもしれないが，本書にも犯人と同じA型だから犯人にされたといった記述が見られ，（当時の）検察の杜撰さが感じられる（「犯人はA型」から「A型だから犯人」は導けない）。

古畑（田中）の表をOCRして目視チェックしたものを abo.xlsx として置いておく。Pythonで読み出してみよう：

import pandas as pd

df = pd.read_excel("https://okumuralab.org/~okumura/stat/data/abo.xlsx")

これで読めたはずだが，合計が合わない：

sum(df['検査人員'][:49])  # 1136456
df['検査人員'][49] - sum(df['検査人員'][:49])  # 12167

血液型の合計は誤差範囲内で100%になっている：

max(abs(df[["O型","A型","B型","AB型"]].sum(axis=1) - 100))  # 0.01

全対象者についてのO，A，B，AB型の比率は 31.51%，37.34%，22.06%，9.10% となっている。都道府県別の対象者人数が人口に比例していないので，都道府県別の割合を人口で重み付けして平均しないといけないが，ここではそこまでやっていない。

この表の「府県名」はJIS X 0401「都道府県コード」の順になっていない。また，当時はまだ沖縄は外地であった。JIS X 0401順に並べ替えるには，次のようにする：

kenmei = ["北海道", "青森", "岩手", "宮城", "秋田", "山形", "福島", "茨城",
          "栃木", "群馬", "埼玉", "千葉", "東京", "神奈川", "新潟", "富山",
          "石川", "福井", "山梨", "長野", "岐阜", "静岡", "愛知", "三重",
          "滋賀", "京都", "大阪", "兵庫", "奈良", "和歌山", "鳥取", "島根",
          "岡山", "広島", "山口", "徳島", "香川", "愛媛", "高知", "福岡",
          "佐賀", "長崎", "熊本", "大分", "宮崎", "鹿児島", "沖縄"]
pref = pd.DataFrame({"id": range(1,48), "都道府県名": kenmei})
df1 = pd.merge(pref, df, left_on="都道府県名", right_on="府県名").drop(columns="府県名")

なお，田中の表には $p$，$q$，$r$ という欄があるが，これについては後述する。

2010年の高校生のデータ

静岡県立磐田南高等学校の生徒さんたちが，全国SSH指定校および理数科設置校にアンケートを依頼され（2010年3月22日付で依頼，返送期限4月末日），41校21017人から得られた回答の集計データをいただくことができた。関係の皆様に感謝する。データの都道府県別人数の部分だけ abo2010.xlsx として置かせていただく。最近のデータとしてはたいへん貴重なものである。

こちらも，JIS X 0401順に並べ替えるには，次のようにする：

df2 = pd.read_excel("https://okumuralab.org/~okumura/stat/data/abo2010.xlsx")
df2 = pd.merge(pref, df2, on="都道府県名")

簡単な集計をしてみる：

s = df2[["計O","計A","計B","計AB"]].sum()
s / sum(s)

結果は次のとおり：

計O     0.297807
計A     0.378646
計B     0.218775
計AB    0.104772

こちらも，本来は都道府県別の割合を人口で重み付けして平均しないといけないが，ここではそこまでやっていない。

これら以外のデータ

天野尹日本に於けるABO式血液型遺伝子頻度の年次及び歴史的変動について（1984年）に1973〜1976年のいくつかの県の献血データによる血液型分布が掲載されている。

私のサイトの血液型と性格の無関連性，またまた血液型と性格にも小規模であるがデータがある。

データの比較

古畑（田中）のデータ，高校生のデータ，冒頭で挙げたツイッターでのアンケート3通りを，グラフで比較してみる。

import matplotlib.pyplot as plt
import numpy as np
from scipy import stats

# n1 = np.round(df[["O型","A型","B型","AB型"]].iloc[49] / 100 * df['検査人員'][49])
n1 = [361931, 428896, 253386, 104525]
# n2 = df2[["計O","計A","計B","計AB"]].sum(axis=0)
n2 = [6259, 7958, 4598, 2202]
n3 = [89326, 102229, 67376, 38469]
n4 = [253, 297, 197, 123]
n5 = [167791, 186333, 116163, 67069]

def prop(a):
    n = sum(a)
    p = np.array(a) / n
    confint = np.array([stats.binomtest(x, n).proportion_ci() for x in a])
    return p, np.array([p - confint[:, 0], confint[:, 1] - p])

x = np.array([1, 2, 3, 4])

p, ci = prop(n1)
plt.errorbar(x, p, ci, fmt="o", label='古畑')

p, ci = prop(n2)
plt.errorbar(x+0.1, p, ci, fmt="o", capsize=5, label='高校生')

p, ci = prop(n3)
plt.errorbar(x+0.2, p, ci, fmt="o", capsize=5, label='@rocinate__')

p, ci = prop(n4)
plt.errorbar(x+0.3, p, ci, fmt="o", capsize=5, label='@dempacat')

p, ci = prop(n5)
plt.errorbar(x+0.4, p, ci, fmt="o", capsize=5, label='@fukada0318')

plt.xticks(x+0.2, ["O","A","B","AB"])
plt.legend()

plt.savefig('abo4.svg', bbox_inches="tight")

エラーバーは95%信頼区間（Rの binom.test() と同じClopper-Pearson流）である。古畑（田中）のデータに比べ，高校生のデータはOが少なくABが多い。ツイッターのアンケート結果は平均に近づいているように見える。ランダムに答えた人がいるのかもしれない。

主成分分析

四つのABO血液型の合計は1であるから，3次元で表せる。これを主成分分析（PCA）で2次元に削減して表示してみる。なお，割合は分散安定化変換 $(2/\pi)\arcsin\sqrt{x}$（拙著『Rで楽しむベイズ統計入門』参照）してから主成分分析するほうがいいかもしれないが，ここでは省略した。

古畑（田中）のデータ：

df1a = df1[["O型","A型","B型","AB型"]]
df1a.index = df1["都道府県名"]

import matplotlib.pyplot as plt
from sklearn.decomposition import PCA

pca = PCA(n_components=2)
x = -pca.fit_transform(df1a)  # 下と合わせるため向きを逆に
pca.explained_variance_ratio_  # array([0.66142869, 0.28123841])

plt.clf()
plt.xlim(min(x[:,0]), max(x[:,0]))
plt.ylim(min(x[:,1]), max(x[:,1]))
for i in range(x.shape[0]):
    plt.text(x[i,0], x[i,1], df1a.index[i],
             horizontalalignment='center', verticalalignment='center')
plt.axis('scaled')

plt.savefig('abo1a.png', bbox_inches="tight")

r = -pca.components_  # 下と合わせるため向きを逆に

plt.clf()
plt.xlim(-1, 1)
plt.ylim(-1, 1)
for i in range(4):
    plt.arrow(0, 0, r[0,i], r[1,i], head_width=0.05,
              head_length=0.05, length_includes_head=True, color='black')
    plt.text(r[0,i], r[1,i], df1a.columns[i])
plt.axis('scaled')

plt.savefig('abo1b.png', bbox_inches="tight")

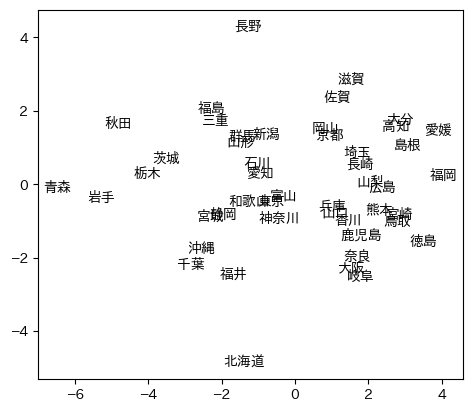
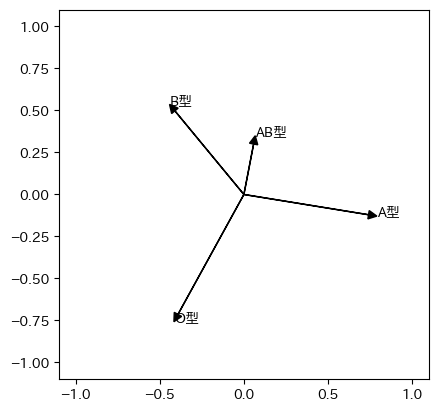
南ほど右側つまりA型が多い。

高校生のデータ：

df2a = df2[["計O","計A","計B","計AB"]]
df2a.index = df2["都道府県名"]
df2a = df2a[df2a.sum(axis=1) != 0]
df2a = df2a.div(df2a.sum(axis=1), axis=0)

pca = PCA(n_components=2)
x = pca.fit_transform(df2a)
pca.explained_variance_ratio_  # array([0.56825035, 0.31448043])

plt.clf()
plt.xlim(min(x[:,0]), max(x[:,0]))
plt.ylim(min(x[:,1]), max(x[:,1]))
for i in range(x.shape[0]):
    plt.text(x[i,0], x[i,1], df2a.index[i],
             horizontalalignment='center', verticalalignment='center')
plt.axis('scaled')

plt.savefig('abo2a.png', bbox_inches="tight")

r = pca.components_

plt.clf()
plt.xlim(-1, 1)
plt.ylim(-1, 1)
for i in range(4):
    plt.arrow(0, 0, r[0,i], r[1,i], head_width=0.05,
              head_length=0.05, length_includes_head=True, color='black')
    plt.text(r[0,i], r[1,i], df2a.columns[i])
plt.axis('scaled')

plt.savefig('abo2b.png', bbox_inches="tight")

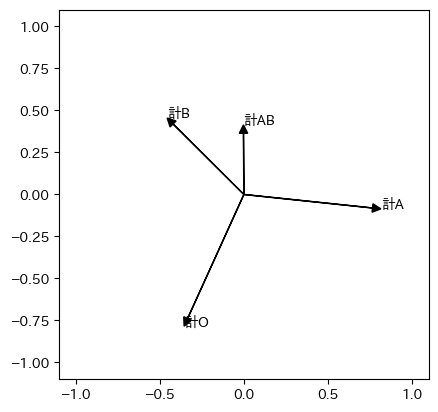
こちらも南ほど右側つまりA型が多い。

遺伝子レベルの分布

A型はA型遺伝子を持ち，B型はB型遺伝子を持ち，AB型は両方の遺伝子を持ち，O型はどちらも持たない。これに基づいて，横軸にA型遺伝子を持つ割合（A+AB），縦軸にB型遺伝子を持つ割合（B+AB）をとってプロットしてみる。青が古畑（田中）のデータ，橙が高校生のデータである。

a1 = (df1["A型"] + df1["AB型"]) / 100
b1 = (df1["B型"] + df1["AB型"]) / 100
a2 = df2a["計A"] + df2a["計AB"]
b2 = df2a["計B"] + df2a["計AB"]

plt.clf()
plt.xlim(min(min(a1),min(a2))-0.001, max(max(a1),max(a2))+0.001)
plt.ylim(min(min(b1),min(b2))-0.001, max(max(b1),max(b2))+0.001)
for i in range(len(a1)):
    plt.text(a1[i], b1[i], df1a.index[i], color="C0",
             horizontalalignment='center', verticalalignment='center')
for i in range(len(a2)):
    plt.text(a2[i], b2[i], df2a.index[i], color="C1",
             horizontalalignment='center', verticalalignment='center')
plt.axis('scaled')
plt.xlabel('A+AB')
plt.ylabel('B+AB')

plt.savefig('abo3.png', bbox_inches="tight")

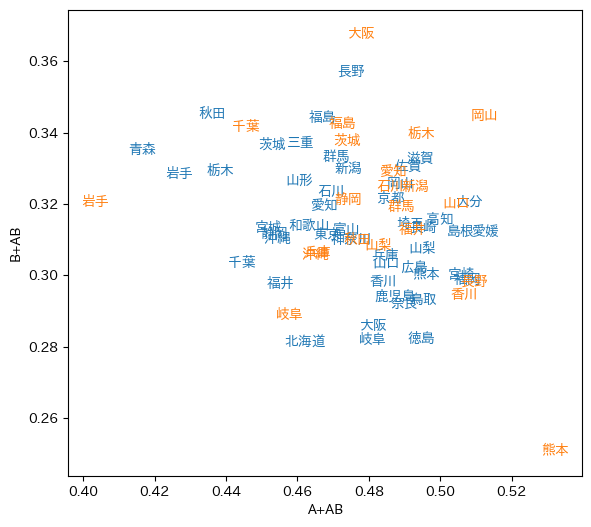
もうちょっと詳しく考えて，古畑の本にある A，B，O 遺伝子の割合 $p$，$q$，$r$ への分解をしてみる。

\[ p + q + r = 1 \] \[ (p + q + r)^2 = \underbrace{p^2 + 2pr}_{\mathrm{A}} + \underbrace{q^2 + 2qr}_{\mathrm{B}} + \underbrace{2pq}_{\mathrm{AB}} + \underbrace{r^2}_{\mathrm{O}} \] \[ r = \sqrt{\mathrm{O}}, \quad p_1 = 1 - \sqrt{\mathrm{B} + \mathrm{O}}, \quad q_1 = 1 - \sqrt{\mathrm{A} + \mathrm{O}} \]

しかし

\[ p_2 = \sqrt{\mathrm{A} + \mathrm{O}} - \sqrt{\mathrm{O}}, \quad q_2 = \sqrt{\mathrm{B} + \mathrm{O}} - \sqrt{\mathrm{O}} \]

でもいいので，平均をとって

\[ p = \frac{p_1 + p_2}{2}, \quad q = \frac{q_1 + q_2}{2} \]

とする。さらに，上に挙げた田中のデータでは，この $p$，$q$，$r$ をそれぞれ10倍された値を使っている。なぜ10倍するかというと，ABOの割合をパーセントで表す場合に都合がよいからである。これを正三角形のグラフで描く方法が古畑の本に紹介されている。Pythonによる三角グラフ（ternary plot）の描き方についてはこのページに解説がある。

奥村晴彦

Last modified: 2024-10-13 21:02:43 JST