[2019-04-04] 最後に追記を書いた。
以下ではABO血液型(表現型,遺伝子型)と性格に有意な関係を示したとする次の論文を紹介する:
Shoko Tsuchimine, Junji Saruwatari, Ayako Kaneda, Norio Yasui-Furukori, “ABO Blood Type and Personality Traits in Healthy Japanese Subjects”, PLOS ONE (2015) DOI:10.1371/journal.pone.0126983
これは2015年当時ネットで話題になったが,豊田秀樹編著『たのしいベイズモデリング』(北大路書房,2018年)の第2章でも取り上げられている。
論文にはデータのExcelファイルが付いていて,これを使えば検証できる?と思ったけれど,論文では年齢・性別でコントロールしてあり,年齢・性別はExcelファイルには含まれていない。
まずはデータを読み込んでみる:
library(readxl)
x = read_excel("journal.pone.0126983.s001.XLSX")
1573×36の表である(論文には1572とある)。names(x) で項目名が一覧できる。以下で使うのは血液型と性格検査の7項目であるので,それだけを抜き出す:
x = x[,c(4,6,11,16,20,21,27,33)]
性格検査の7項目はそれぞれ NS (Novelty Seeking), HA (Harm Avoidance), RD (Reward Dependence), P (Persistence), SD (Self-directedness), C (Cooperativeness), ST (Self-transcendence) である。
これら全変数が揃っているものだけ抜き出そう:
x = subset(x, complete.cases(x))
これで1426行に減る(論文では1427とされている)。
この表の「Blood types」は遺伝子型(AA, AB, AO, BB, BO, OO)で,これらに対応する表現型はそれぞれ A, AB, A, B, B, O である。遺伝子型を表現型に変換するには,Rではいろいろなやりかたがあるが,@hoxo_m さんのRでハッシュテーブルの速度比較を参考に,ここでは一番簡単な名前付きベクトルを使うことにする:
tbl = c("A","AB","A","B","B","O") # 表現型
names(tbl) = c("AA","AB","AO","BB","BO","OO") # 遺伝子型
x$ABO = tbl[x[[1]]] # 表現型を表に追加
論文では年齢・性別でコントロールしたMANCOVAが使われているが,年齢・性別がわからないので,ここでは単なるMANOVAを使ってみる:
r1 = manova(cbind(NS,HA,RD,P,SD,C,ST) ~ `Blood types`, data=x)summary(r1)Df Pillai approx F num Df den Df Pr(>F)`Blood types` 5 0.027593 1.1241 35 7090 0.2822Residuals 1420r2 = manova(cbind(NS,HA,RD,P,SD,C,ST) ~ ABO, data=x)summary(r2)Df Pillai approx F num Df den Df Pr(>F)ABO 3 0.01985 1.3493 21 4254 0.1318Residuals 1422
いずれも有意ではない(Pillai 以外の方法については manova() のマニュアル参照)。
論文では特に Persistence(「持続」)が血液型と有意に関係するとされているので,それを計算してみる:
oneway.test(P ~ `Blood types`, data=x)One-way analysis of means (not assuming equal variances)data: P and `Blood types`F = 2.5173, num df = 5.00, denom df = 285.15, p-value = 0.02993oneway.test(P ~ ABO, data=x)One-way analysis of means (not assuming equal variances)data: P and ABOF = 2.714, num df = 3.00, denom df = 483.28, p-value = 0.04434
論文ではそれぞれ p = 0.020, 0.032 だが,年齢・性別でコントロールしていないためか,ここでの計算結果は p = 0.030, 0.044 となった。しかし,7変数のうち1変数である。多重性まで考えれば,有意な結果が得られたとは言い難い。
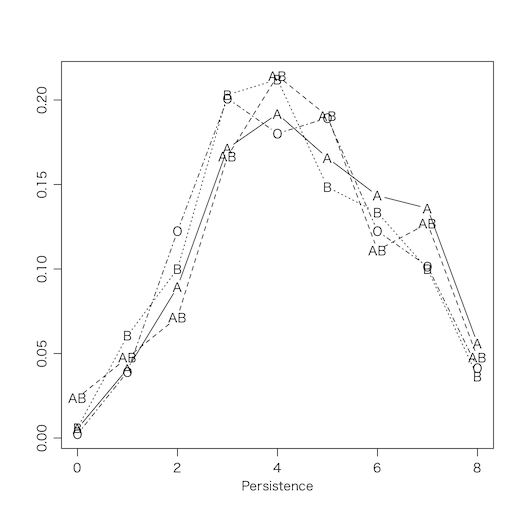
Persistence の度数分布は次の通りである。これを見てもあまり意味のある差がありそうにない。
a = names(table(x$ABO))
p = sapply(a, function(b) { t = table(subset(x, ABO==b)$P); t / sum(t) })
matplot(0:8, p, type="b", pch=" ", col="black", xlab="Persistence", ylab="")
sapply(a, function(b) text(0:8, p[,b], b))

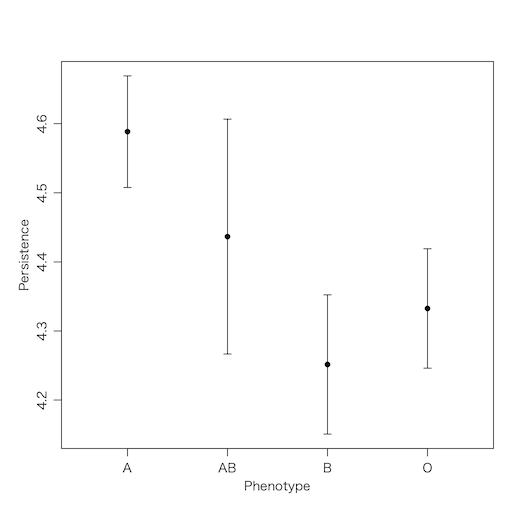
血液型ごとに平均±標準誤差をエラーバーで表してみる:
n = table(x$ABO)
m = sapply(names(n), function(a) mean(subset(x, ABO==a)$P))
s = sapply(names(n), function(a) sd(subset(x, ABO==a)$P))
se = s / sqrt(n)
plot(1:4, m, pch=16, xlim=c(0.5,4.5), ylim=range(c(m+se,m-se)),
xaxt="n", xlab="Phenotype", ylab="Persistence")
arrows(1:4, m-se, 1:4, m+se, length=0.05, angle=90, code=3)
axis(1, at=1:4, labels=names(n))
[2019-04-04追記] ご質問をいただいたので,補足する。