「95%信頼区間とは,真の値が入る確率が95%の区間のことです」というような説明をすることがあります。私も,一般のかたに説明するときは,ついそのように言ってしまうことがあります。でも本当は真っ赤なウソです。主観確率を扱うベイズ統計学はここでは考えません。
正規分布では,ウソの考え方をしても結論が同じになることがあるので,ここではわざと,左右非対称なポアソン分布を考えます。
ポアソン分布とは,1日に起こる地震の数,1時間に窓口を訪れるお客の数,1分間に測定器に当たる放射線の数などを表す分布です。平均 $\lambda$ のポアソン分布の確率分布は次の式で表されます:
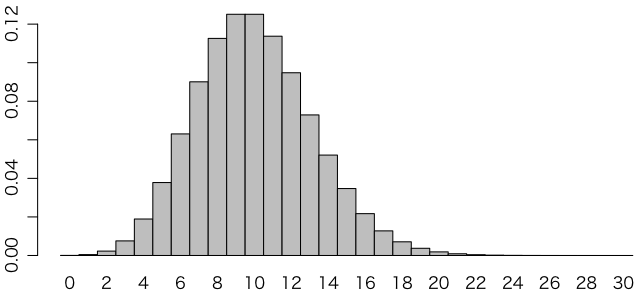
\[ p_k = \frac{\lambda^k e^{-\lambda}}{k!} \]$\lambda = 10$ のポアソン分布の確率分布をグラフにすると次のようになります(本当は右に無限に延びるのですが,$k = 30$ までしか表示していません):

これは,平均して1分間に10個の放射線を出すものがあれば,1分だけ観測したときに,ぴったり9個観測する確率は約0.125,ぴったり10個観測する確率も約0.125,ぴったり11個観測する確率は約0.114,…といったことを表します。
この逆の「もし1分間に10個の放射線を観測したとすれば,1分あたりの放射線の平均個数の真の値は上のグラフのように分布する」という考え方はウソです。
では,1分間に10個の放射線を観測した場合の,1分あたりの放射線の平均個数の「95%信頼区間」とは,何を意味しているのでしょうか?
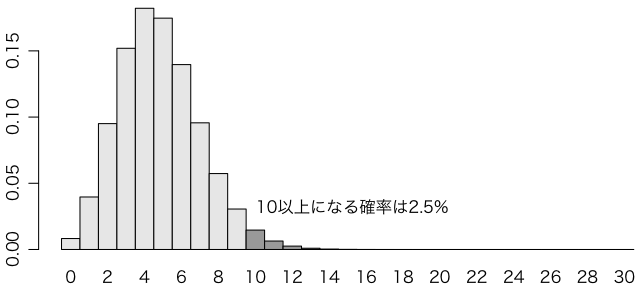
まず,ポアソン分布の平均 $\lambda$ を少しずつ小さくしてみます。だいたい $\lambda = 4.8$ にしたところで,10以上の値が出る確率が2.5%になります。
今度は,ポアソン分布の平均 $\lambda$ を少しずつ大きくしてみます。だいたい $\lambda = 18.4$ にしたところで,10以下の値が出る確率が2.5%になります。
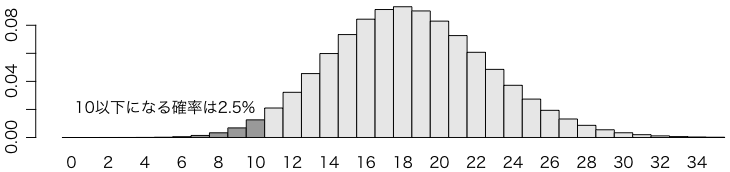
このように,$\lambda = 4.8$ のポアソン分布と,$\lambda = 18.4$ のポアソン分布は,それぞれ10以上,10以下の部分の片側確率が2.5%になります。統計学では一般に両側確率のほうをよく使いますので,2倍して両側確率5%と考えると,$\lambda = 4.8$ のポアソン分布と,$\lambda = 18.4$ のポアソン分布は,どちらもぎりぎり「10」という値と5%水準で矛盾しない分布です(中央の95%の部分にぎりぎり「10」が含まれます)。この意味で,$4.8 \leq \lambda \leq 18.4$ を「平均個数 $\lambda$ の95%信頼区間」と呼びます。
一般に,信頼区間は,観測値(ここでは10)について左右対称ではありません。
信頼区間は,観測値(測定値)とその誤差を表すための一つの方法です。別の(もっと簡便な)方法として,ポアソン分布なら「観測値 $\pm$ その平方根」(この場合は $10 \pm \sqrt{10}$)を使うこともありますが,これはほぼ68%信頼区間を左右対称にしたものになります。平均 $\lambda$ のポアソン分布の標準偏差は正確に $\sqrt{\lambda}$ ですから,$\lambda$ を測定値で代用したことに相当します。
[2022-10-16 訂正] $4.8 \geq \lambda \geq 18.4$ となっていましたが不等号が逆でした。いま直しました。10年間気づかなかったorz