赤ちゃんに毎日保湿剤 アトピー減 | NHK「かぶん」ブログによると,アトピー性皮膚炎になった家族がいる新生児118人を無作為に2分し,一方には保湿剤を毎日全身に塗ったところ,保湿剤を塗った群では19人,対照群は28人がアトピー性皮膚炎になった。保湿剤には発症のリスクを32%抑える効果があると証明できた。
本当かな。
fisher.test(matrix(c(19,28,40,31), nrow=2))
としても,$p=0.1321$ にしかならないぞ。
元論文 Application of moisturizer to neonates prevents development of atopic dermatitis - Journal of Allergy and Clinical Immunology は三重大で購読していたので読んでみた。Kaplan-Meier法で $p=0.012$ とのこと。
この間の事情は,自称、統計学をやっていますとドヤ顔するものなのでに詳しく書いていただいている。
要は,最終的な発症数の比較だけでなく,日々の発症数を詳しく解析すれば,より精密な結果が出るというわけである。
ここで扱う「survival analysis」は,生存分析,生存時間分析,生存時間解析といった訳語があるが,ここでは次の入門書に従って「生存時間解析」と呼ぶことにする。
「生存時間」というと,生死を扱うように聞こえるが,副題の time to event つまり「何らかの事象までの時間」というほうが正確である。プロローグで述べた新生児のアトピー性皮膚炎発症までの時間や,鉄棒の練習を始めてから逆上がりができるまでの時間など,多くの場合に使える。ここで重要なのは,途中で観測対象から外れる場合を考慮しなければならないことである。
Rで生存時間解析を行うパッケージとして,以下では survival を使う。
install.packages("survival")
library(survival)
上述の入門書では,例としてWorcester Heart Attack Studyの100人分のデータ(WHAS100)を使っている。このデータはRの survMisc パッケージにも収められている。
install.packages("survMisc")
library(survMisc)
data(whas100)
データ whas100 の各項目の意味:
admitdatefoldateloslenfolfstatagegenderbmi追跡総期間の順に最初と最後を表示してみる:
> o = order(whas100$lenfol)
> head(whas100[o,])
id admitdate foldate los lenfol fstat age gender bmi
1 1 3/13/1995 3/19/1995 4 6 1 65 0 31.38134
31 31 9/3/1995 9/9/1995 4 6 1 72 0 27.97907
56 56 9/1/1997 9/15/1997 11 14 1 64 1 24.41255
85 85 12/2/1997 1/15/1998 3 44 1 71 0 23.05630
98 98 11/26/1997 1/27/1998 8 62 1 86 1 14.91878
53 53 8/20/1997 11/17/1997 3 89 1 87 1 18.77718
> tail(whas100[o,])
id admitdate foldate los lenfol fstat age gender bmi
18 18 10/30/1995 1/5/2003 9 2624 1 61 0 30.71420
27 27 10/18/1995 12/31/2002 2 2631 0 68 0 26.44693
11 11 10/11/1995 12/31/2002 6 2638 0 73 1 28.43344
16 16 10/8/1995 12/31/2002 5 2641 0 39 0 30.10881
33 33 7/22/1995 12/22/2002 8 2710 1 81 1 28.64898
10 10 7/22/1995 12/31/2002 9 2719 0 40 0 21.78971
最初の人(id = 1)は,1995年3月13日に入院したときから観察を開始し,6日後(lenfol = 6)に死亡(fstat = 1)した。一方,最後の人(id = 10)は,1995年7月22日に入院したときから観察を開始し,2719日後(lenfol = 2719)の2002年12月31日に観察を終了した時点では生存(fstat = 0)している。
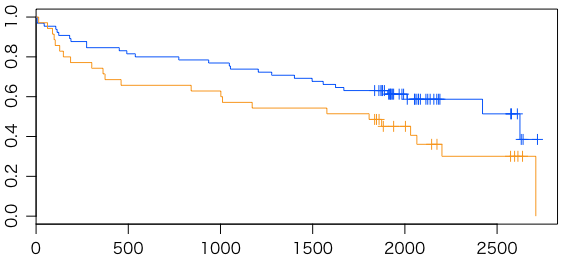
このように,入院日(観察開始日)は人それぞれであるが,これを0日目として,男女別に,生存割合をプロットしてみると,次のようになる:
s = survfit(Surv(lenfol, fstat) ~ gender, data=whas100)
plot(s, col=c("#0041ff","#ff9900"))

上で ~ gender を ~ 1 とすれば,男女に分けずに,全体の生存曲線とその95%信頼区間をプロットする。
上で Surv(lenfol, fstat) は survival オブジェクトというものを作るための関数である。試しに Surv(whas100$lenfol, whas100$fstat) または同じことであるが with(whas100, Surv(lenfol, fstat)) と打ち込んでみれば,次のように出力される:
[1] 6 374 2421 98 1205 2065 1002 2201 189 2719+ 2638+ 492
[13] 302 2574+ 2610+ 2641+ 1669 2624 2578+ 2595+ 123 2613+ 774 2012
[25] 2573+ 1874 2631+ 1907 538 104 6 1401 2710 841 148 2137+
[37] 2190+ 2173+ 461 2114+ 2157+ 2054+ 2124+ 2137+ 2031 2003+ 2074+ 274
[49] 1984+ 1993+ 1939+ 1172 89 128 1939+ 14 1011 1497 1929+ 2084+
[61] 107 451 2183+ 1876+ 936 363 1048 1889+ 2072+ 1879+ 1870+ 1859+
[73] 2052+ 1846+ 2061+ 1912+ 1836+ 114 1557 1278 1836+ 1916+ 1934+ 1923+
[85] 44 1922+ 274 1860+ 1806 2145+ 182 2013+ 2174+ 1624 187 1883+
[97] 1577 62 1969+ 1054
この 2719+ は少なくとも2719日生存したということを表す。
男(青)より女(オレンジ)のほうが生存者の割合が速く減少していることがわかる。グラフの短い縦線は,その時点で生存しながら観察期間を終えた人がいることを表す。このような図をKaplan-Meier(カプラン・マイヤー)プロット((生存)曲線)という(WikipediaのKaplan–Meier estimator参照)。
このグラフの表すものは,母集団の「生存関数」の推定値(Kaplan-Meier推定値)である。これは,初期値を1として,次のように計算する:第 $i$ 日の最初に観察中の人が $n_i$ 人いて,その日のうちに $d_i$ 人が死亡したとすると,第 $i$ 日の値は第 $i-1$ 日の値の $\dfrac{n_i - d_i}{n_i}$ 倍である。日付が変わると,分母 $n_i$ は死亡数と観察終了数だけ減る。観察終了は,観察期間が終了するか,対象者が何らかの理由で観察対象から外れたときに生じる。
この男女差を統計的に検定するには,survdiff() 関数を使う:
> survdiff(Surv(lenfol, fstat) ~ gender, data=whas100)
Call:
survdiff(formula = Surv(lenfol, fstat) ~ gender, data = whas100)
N Observed Expected (O-E)^2/E (O-E)^2/V
gender=0 65 28 34.6 1.27 3.97
gender=1 35 23 16.4 2.68 3.97
Chisq= 4 on 1 degrees of freedom, p= 0.0463
デフォルトではログランク検定(log-rank test)が行われる。$p = 0.0463$ である。
survdiff() は $p$ 値を表示するが,ほかで使うために $p$ 値だけ取り出すには,次のようにすればよい:
pchisq(survdiff(Surv(lenfol, fstat) ~ gender, data=whas100)$chisq, 1, lower.tail=FALSE)
ヘルプ ?survdiff によれば,survdiff() のデフォルトオプション rho=0 では the log-rank (Mantel-Haenszel) test が行われ,rho=1 では the Peto & Peto modification of the Gehan-Wilcoxon test が行われるとのこと。
この log-rank 検定は次のような手順で行われる。まず初期値は男女それぞれ65人,35人である。5日目までは何も起こらないが,6日目に2人死亡し,2人とも男性である。この確率は,フィッシャーの正確検定のところで述べたものとまったく同じで,壷の中に男女それぞれ65人,35人が入っており,ランダムに2人取り出したときの分布(超幾何分布)である:
| 男 | 女 | |
|---|---|---|
| 取り出した | 2 | 0 |
| まだ壷の中 | 63 | 35 |
この確率は $\dfrac{{}_{65}C_2 \cdot {}_{35}C_0}{{}_{100}C_2} = 0.420202$ である。同様に,
| 男 | 女 | |
|---|---|---|
| 取り出した | 1 | 1 |
| まだ壷の中 | 64 | 34 |
は $\dfrac{{}_{65}C_1 \cdot {}_{35}C_1}{{}_{100}C_2} = 0.459596$,
| 男 | 女 | |
|---|---|---|
| 取り出した | 0 | 2 |
| まだ壷の中 | 65 | 33 |
は $\dfrac{{}_{65}C_0 \cdot {}_{35}C_2}{{}_{100}C_2} = 0.120202$ で,当然ながら合計すると 1 になる。死亡する男の人数の期待値は $0.420202 \times 2 + 0.459596 \times 1 + 0.120202 \times 0 = 1.3$ であるが,これは当然ながら $2 \times 65 / 100$ でも求められる。
男の死亡数の分散は $0.420202 \times (2 - 1.3)^2 + 0.459596 \times (1 - 1.3)^2 + 0.120202 \times (0-1.3)^2 = 0.450404$ である。
一般に,$n_1 + n_2 = n$ 人のうち $d$ 人が死亡するなら,片方の期待値は $dn_1/n$ であり,分散は
\[ V = \frac{n_1}{n} \cdot \frac{n_2}{n} \cdot \frac{d(n-d)}{n-1} \]である。これらを,死亡が観測されたすべての日 $i$ について計算すれば,
\[ \frac{\sum (d_i - d_i n_{1i} / n_i)}{\sqrt{\sum V_i}} \] は標準正規分布 $N(0, 1)$ に従うことを使って検定ができる。あるいは,上の式の2乗が自由度1のカイ2乗分布に従うとしてもよい。これがsurvdiff() のやっていることである。
ところで,上の話は59人×2のグループで47人が発症し,その2×2表は fisher.test() では有意にならず生存時間解析のログランク検定で有意になった。これらの関係はどうなっているのだろう?
foo = function() {
x = matrix(59, 59, 2)
y = matrix(0, 59, 2)
z = matrix(0:1, 59, 2, byrow=TRUE)
for (i in 1:47) {
j = sample(2, 1)
x[i, j] = i
y[i, j] = 1
}
chi2 = survdiff(Surv(as.vector(x), as.vector(y)) ~ as.vector(z))$chisq
p1 = pchisq(chi2, 1, lower.tail=FALSE)
p2 = fisher.test(matrix(c(sum(y[,1]), 59-sum(y[,1]), sum(y[,2]), 59-sum(y[,2])), nrow=2))$p.value
c(p1, p2)
}
a = replicate(1000, foo())
plot(a[1,], a[2,], xlab="log-rank test", ylab="Fisher test", asp=1)
おっと,発症数47固定では fisher.test() の特徴的な離散構造が出過ぎてしまい,$p$ 値が不正確になってしまう。発症数を固定せず,どれも47/118の確率で発症するとしてみよう。
foo = function() {
x = matrix(1, 59, 2)
y = matrix(0, 59, 2)
z = matrix(0:1, 59, 2, byrow=TRUE)
for (i in 1:118) {
if (runif(1) < 47/118) {
x[i] = runif(1)
y[i] = 1
}
}
chi2 = survdiff(Surv(as.vector(x), as.vector(y)) ~ as.vector(z))$chisq
p1 = pchisq(chi2, 1, lower.tail=FALSE)
p2 = fisher.test(matrix(c(sum(y[,1]), 59-sum(y[,1]), sum(y[,2]), 59-sum(y[,2])), nrow=2))$p.value
c(p1, p2)
}
a = replicate(1000, foo())
plot(a[1,], a[2,], xlab="log-rank test", ylab="Fisher test", asp=1)
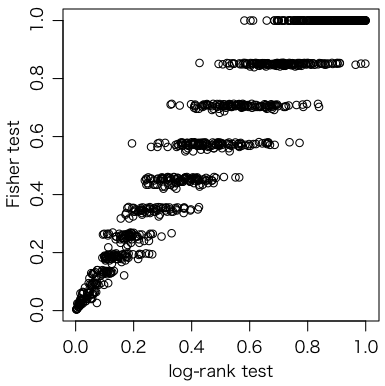
離散構造はまだ見えるが,こちらのほうがよい。
ログランク検定のほうが有意になりやすいということはないのか。試してみよう:
a = replicate(100000, foo())
mean(a[1,] < 0.05) # ログランク検定が5%有意になる確率→ほぼ0.05
mean(a[2,] < 0.05) # fisher.test()が5%有意になる確率→ほぼ0.03
fisher.test() はやや保守的になり,有意になりにくい。ログランク検定はほぼ想定通りだ。
Last modified: