Stirlingの公式

教授に「スターリングの近似は本当に凄く良い近似だよ」と言われて確かめてみたら…というツイートを見かけたので私もやってみた。

Stirlingの公式

\[ x! = \Gamma(x+1) \approx \sqrt{2\pi x} \, x^x e^{-x} \]

をRでプロットするだけである：

curve(gamma(x+1), xlim=c(0,10), log="y", col="#0068b7", xlab="", ylab="")
curve(sqrt(2*pi*x) * x^x * exp(-x), add=TRUE, col="#f39800")
curve(sqrt(2*pi*x) * x^x * exp(-x) * (1 + 1/(12*x)), add=TRUE, col="#f39800")

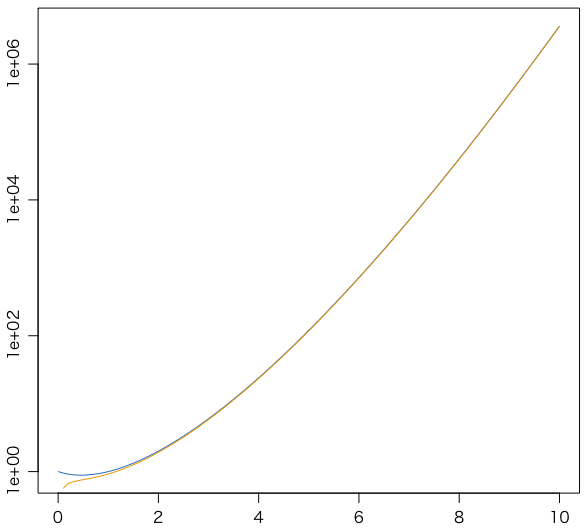
青が $\Gamma(x+1)$，橙がStirlingの近似である。

Stirling formula

さらに正確な式

\[ x! = \Gamma(x+1) \approx \sqrt{2\pi x} \, x^x e^{-x} \left(1 + \frac{1}{12x} \right) \]

も含めて，詳しくは黒木玄さんのガンマ分布の中心極限定理とStirlingの公式に詳しい解説がある。黒木玄さんはさらに，Kullback-Leibler情報量に関する解説で，多項分布のStirling近似（の対数の $-n$ 倍）がKullback-Leibler情報量になることを導出されている。