イノシシはロングテール？

ロングテールといっても，本物の尻尾の長さではなく，分布の裾の長さのことです。

厚労省の「食品中の放射性物質の検査結果について」（日報）をデータベース化している私の食品の放射能データ検索でイノシシの放射性セシウム（Cs）のBq/kg値を調べてみましょう。ND（不検出）以外のデータを調べるには，Cs-134・Cs-137合計値の欄を「1 Bq/kg以上」にして検索するのが簡単です。2013年8月14日までのデータでは873件あります。

この分布を調べてみましょう。Webの検索結果をそのまま使ってもいいのですが，ここではすべてR（またはExcel）でやってみましょう。

まず，全データを取得します。http://okumuralab.org/~okumura/stat/data/mhlw/ にある「merged.csv.gz」という圧縮ファイルをダウンロードして展開するのが簡単でしょう。

展開したファイル「merged.csv」をRで読み込むには次のようにします。

data = read.csv("merged.csv", header=FALSE, as.is=TRUE)

ヘッダ行がないので header=FALSE と指定しています。as.is=TRUE は，なくてもいいのですが，これを指定すると，数値以外の列を文字列として扱います。これを指定しないと，数値以外を因子（ファクター）として扱います。

Excelを使う場合は，UTF-8のmerged.csvをそのままダブルクリックして開くと文字化けしますので，いったん「メモ帳」などのテキストエディタで開いて文字コード「シフトJIS」で保存し直してから開いてください。「メモ帳」では「ANSI」と書いてあるのが「シフトJIS」（を拡張したWindowsの文字コード）です。

以下はRで説明します。まず品目名が「イノシシ」を含むデータを抽出します。

ino = subset(data, grepl('イノシシ', V10))

dim(ino) で調べてみると1019件あります（2013年8月14日時点）。19列目 ino$V19 がCs合計値ですが，<20 のような不検出（ND）がありますので，文字列扱いになってしまっています。これをまず数値に変換します。

inocs = as.numeric(ino$V19)

数値に変換できない <20 のようなものは「NA」（not available）というRの特別な値に変換されます。

イノシシの例はこれで大丈夫なのですが，ぴったり「0」というありえない値が出現することがありましたので，念のため0以下の値を「NA」に直します。

inocs = ifelse(inocs <= 0, NA, inocs)

「NA」の扱いはいろいろ考えられますが，ここでは単に「NA」を削除することにします。

inocs = na.omit(inocs)

length(inocs) で長さを調べてみると，ちょうど873で，Webでの検索結果と一致します。

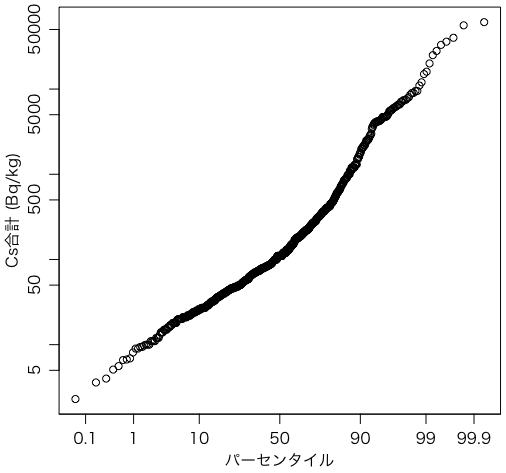
この分布を「正規確率プロット」で描いてみます。

par(mgp=c(2,0.8,0))  # 特に必要ない描画パラメータの調整
qqnorm(inocs, log="y", xlab="パーセンタイル",
       ylab="Cs合計 (Bq/kg)", xaxt="n", main="イノシシ")
p = c(0.01, 0.1, 1, 10, 50, 90, 99, 99.9, 99.99)
axis(1, at=qnorm(p/100), labels=p)

この qqnorm() 関数は，正規分布のときにプロットが直線になるように横軸の目盛りをとったプロットを描きます。ここでは縦軸を対数（log="y"）にしましたので，プロットが直線になれば，分布は対数正規分布です。非常におおまかですがイノシシの放射能は対数正規分布に従うことがわかります。

対数正規分布は，分布の裾（尻尾）が長い「ロングテール」な分布の一つです。

plot(qnorm((1:873-0.5)/873), sort(inocs), log="y")

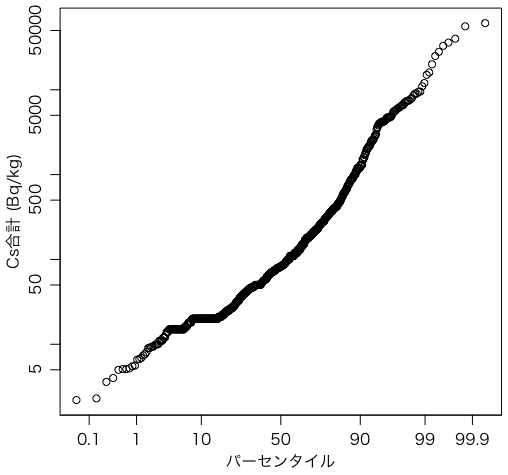
上の解析では <20 のような文字列は無視しましたが，これを上限の 20 で置き換えるという考え方もありえます。そのようにするには，

inocs = as.numeric(sub("<", "", inocs))

とすればいいでしょう。こうすれば件数は 1019 になります。正規確率プロットは次のようになります。

ちなみに，このようなロングテールの分布は，横軸を（着目する側から数えた）順位にして，両対数でプロットすることがよくあります。

plot(1:873, sort(inocs,decreasing=TRUE), log="xy",
     xlab="順位", ylab="Cs合計 (Bq/kg)")

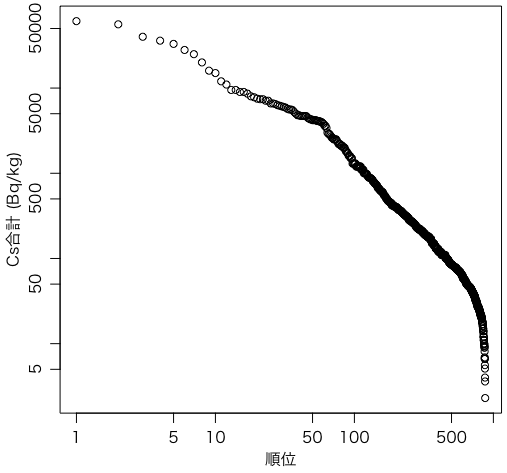
このプロットが直線であれば，値 = 順位^-s のような「べき乗則」に従います。「順位」はさきほどの正規確率プロットのように0.5，1.5，…（または 5/8，13/8，…）とすべきかもしれませんが，ここでは単純に1，2，…としました。

奥村 晴彦

Last modified: 2013-08-15 17:05:26