Efron--Morris (1975) の野球データ

Bradley Efron and Carl Morris, “Data analysis using Stein's estimator and its generalizations”, Journal of the American Statistical Association, Vol. 70, No. 350, pp. 311--319 (1975) という有名な論文に掲載された1970年の大リーグ選手18人の打率データを扱う。このデータは例えばパッケージ pscl に含まれている：

install.packages("pscl")
library(pscl)
EfronMorris
               name  team league  r     y   n     p
1  Roberto Clemente Pitts     NL 18 0.400 367 0.346
2    Frank Robinson  Balt     AL 17 0.378 426 0.298
3      Frank Howard  Wash     AL 16 0.356 521 0.276
4     Jay Johnstone   Cal     AL 15 0.333 275 0.222
5         Ken Berry   Chi     AL 14 0.311 418 0.273
6       Jim Spencer   Cal     AL 14 0.311 466 0.270
7     Don Kessinger   Chi     NL 13 0.289 586 0.263
8     Luis Alvarado   Bos     AL 12 0.267 138 0.210
9         Ron Santo   Chi     NL 11 0.244 510 0.269
10      Ron Swoboda    NY     NL 11 0.244 200 0.230
11        Del Unser  Wash     AL 10 0.222 277 0.264
12   Billy Williams   Chi     AL 10 0.222 270 0.256
13     George Scott   Bos     AL 10 0.222 435 0.303
14  Rico Petrocelli   Bos     AL 10 0.222 538 0.264
15  Ellie Rodriguez    KC     AL 10 0.222 186 0.226
16  Bert Campaneris   Oak     AL  9 0.200 558 0.285
17   Thurman Munson    NY     AL  8 0.178 408 0.316
18        Max Alvis   Mil     NL  7 0.156  70 0.200

選手名，チーム名，リーグ名，シーズン最初の45打席の打数と打率，シーズン残りの打席数と打率である。

これをベイズ統計の階層モデルで扱う。

「45打席で何安打か」のデータ EfronMorris$r は2項分布であるが，ここでは打率 $x_i =$ EfronMorris$r / 45 を「分散安定化変換」$y_i = \arcsin\sqrt{x_i}$ で変換し，正規分布として扱う。変換後の値 $y_i$ の誤差分散はおおよそ $\sigma_i^2 = 1/(4 \times 45)$ である。パッケージ bayesmeta を使い，階層モデル $y_i \sim \mathcal{N}(\theta_i, \sigma_i^2)$, $\theta_i \sim \mathcal{N}(\mu, \tau^2)$ のパラメータを推定する。$\tau^2$ の事前分布としては Jeffreys（reference prior）を使う（詳細は拙著『Rで楽しむベイズ統計入門』参照）。Jeffreys にする意味がわからなければ，例えば $\tau$ についての一様分布 tau.prior="uniform" を選べばよい（「一様分布」といっても $\tau$ についての一様分布，$\tau^2$ についての一様分布，$\log\tau$ についての一様分布はみな異なることに注意）。

library(bayesmeta)
x = asin(sqrt(EfronMorris$r/45))
rj = bayesmeta(x, rep(sqrt(1/(4*45)),18), tau.prior="Jeffreys")
rj
 'bayesmeta' object.

18 estimates:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, ...

tau prior (improper):
Jeffreys prior 

mu prior (improper):
uniform(min=-Inf, max=Inf)

ML and MAP estimates:
                    tau        mu
ML joint     0.01721052 0.5382009
ML marginal  0.02533541 0.5382009
MAP joint    0.03772003 0.5382052
MAP marginal 0.04057119 0.5381961

marginal posterior summary:
                  tau         mu
mode      0.040571193 0.53819614
median    0.044226348 0.53819614
mean      0.046411283 0.53819614
sd        0.022868462 0.02139456
95% lower 0.004986711 0.49602413
95% upper 0.089562012 0.58034776

(quoted intervals are shortest credible intervals.)

$\theta_i$ の推定値は次のようになる：

rj$theta
                   1          2          3          4          5          6
y         0.68471920 0.66192481 0.63886514 0.61547971 0.59170064 0.59170064
sigma     0.07453560 0.07453560 0.07453560 0.07453560 0.07453560 0.07453560
mode      0.55740871 0.55441538 0.55137904 0.54833323 0.54521442 0.54521442
median    0.57239361 0.56683805 0.56132255 0.55583188 0.55034068 0.55034068
mean      0.57860783 0.57232104 0.56596109 0.55951128 0.55295291 0.55295291
sd        0.04879022 0.04691727 0.04528419 0.04392679 0.04288433 0.04288433
95% lower 0.49227083 0.48777295 0.48257799 0.47671781 0.47010477 0.47010477
95% upper 0.68070908 0.67096015 0.66135150 0.65195235 0.64270709 0.64270709
                   7          8          9         10         11         12
y         0.56745048 0.54263910 0.51715966 0.51715966 0.49088268 0.49088268
sigma     0.07453560 0.07453560 0.07453560 0.07453560 0.07453560 0.07453560
mode      0.54202584 0.53877748 0.53544334 0.53544334 0.53201210 0.53201210
median    0.54481251 0.53919945 0.53344197 0.53344197 0.52746871 0.52746871
mean      0.54626461 0.53942153 0.53239419 0.53239419 0.52514689 0.52514689
sd        0.04219794 0.04190868 0.04205521 0.04205521 0.04267204 0.04267204
95% lower 0.46274308 0.45460402 0.44572443 0.44572443 0.43605293 0.43605293
95% upper 0.63365466 0.62481336 0.61628872 0.61628872 0.60812869 0.60812869
                  13         14         15         16         17         18
y         0.49088268 0.49088268 0.49088268 0.46364761 0.43524991 0.40542062
sigma     0.07453560 0.07453560 0.07453560 0.07453560 0.07453560 0.07453560
mode      0.53201210 0.53201210 0.53201210 0.52844998 0.52471905 0.52079193
median    0.52746871 0.52746871 0.52746871 0.52119635 0.51452968 0.50736158
mean      0.52514689 0.52514689 0.52514689 0.51763534 0.50980313 0.50157608
sd        0.04267204 0.04267204 0.04267204 0.04378903 0.04543292 0.04763146
95% lower 0.43605293 0.43605293 0.43605293 0.42551225 0.41409413 0.40159214
95% upper 0.60812869 0.60812869 0.60812869 0.60039459 0.59326275 0.58675914

実際の打率に直すには，分散安定化変換の逆変換 $\sin^2 \theta_i$ が必要であるが，ここではこのままの値を使う。

同様に，標準偏差 $\tau$ について一様な事前分布，$\sqrt{\tau}$ について一様な事前分布も試してみる。

ru = bayesmeta(x, rep(sqrt(1/(4*45)),18), tau.prior="uniform")
rs = bayesmeta(x, rep(sqrt(1/(4*45)),18), tau.prior="sqrt")

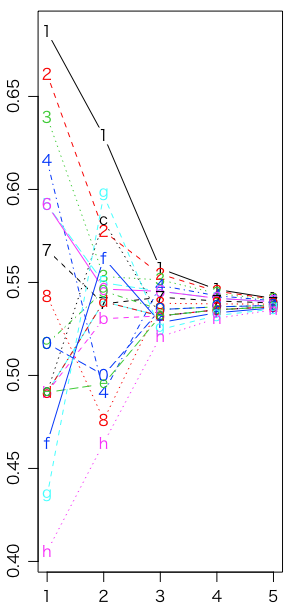
最初の45打席の打率，シーズン残りの打率，Jeffreys，uniform，sqrt の比較である（グラフはそれぞれモード，中央値，平均値）：

z = asin(sqrt(EfronMorris$p))
matplot(1:5, rbind(x,z,rj$theta[3,],ru$theta[3,],rs$theta[3,]), type="b", xlab="", ylab="") # モード
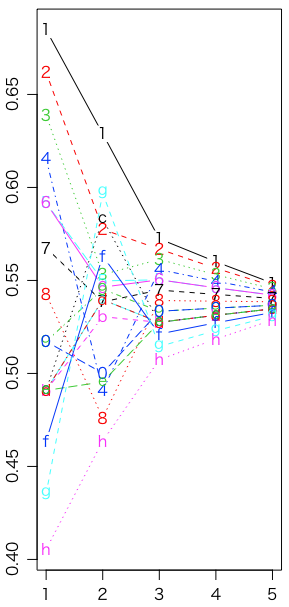
matplot(1:5, rbind(x,z,rj$theta[4,],ru$theta[4,],rs$theta[4,]), type="b", xlab="", ylab="") # 中央値
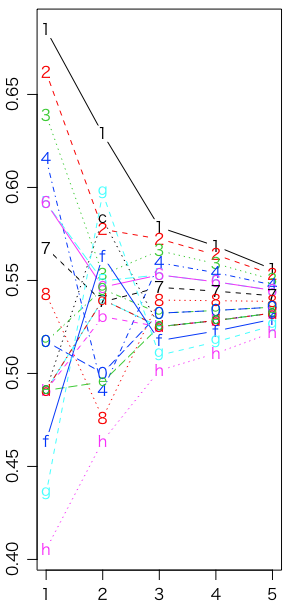
matplot(1:5, rbind(x,z,rj$theta[5,],ru$theta[5,],rs$theta[5,]), type="b", xlab="", ylab="") # 平均値

ご覧のように（あるいは var(rj$theta[3,]) 等で確認できるように），Jeffreysの分散が一番大きく，その中でもモードより中央値，中央値より平均値のほうが分散が大きい。見た感じでは分散が大きいほうが予測すべきシーズン残りの打率に近そうだが，実際には僅差である：

mean((z - rj$theta[3,])^2)
[1] 0.001556614
mean((z - rj$theta[4,])^2)
[1] 0.001543662
mean((z - rj$theta[5,])^2)
[1] 0.001587429
mean((z - ru$theta[3,])^2)
[1] 0.001643058
mean((z - ru$theta[4,])^2)
[1] 0.001544991
mean((z - ru$theta[5,])^2)
[1] 0.001542212
mean((z - rs$theta[3,])^2)
[1] 0.00169758
mean((z - rs$theta[4,])^2)
[1] 0.001618288
mean((z - rs$theta[5,])^2)
[1] 0.001563295

比較のため，最初の45打席の結果をそのまま使うと，これらよりずっと大きな予測誤差になる：

mean((z - x)^2)
[1] 0.00542305

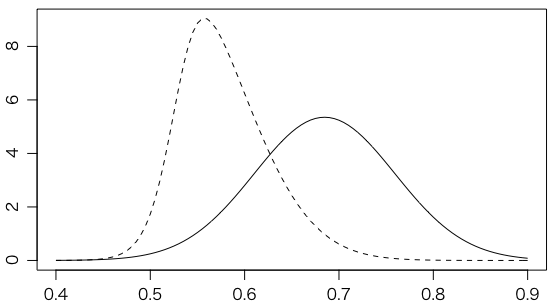
もうちょっと具体的に，1番のClementeは当初打率トップだが，誤差を考えれば，下図の実線のような分布になる。18人の中心に収縮させたものが破線である（Jeffreysの場合）。

curve(rj$dposterior(theta=x, individual=1), 0.4, 0.9, lty=2, xlab="", ylab="")
curve(dnorm(x, rj$theta[1,1], rj$theta[2,1]), add=TRUE)

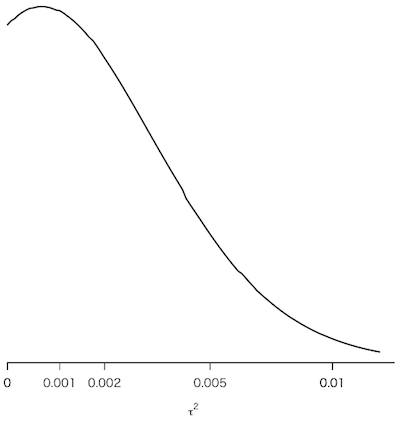
ついでに『Rで楽しむベイズ統計入門』図6.3に相当するものを描いておく：

ydata = asin(sqrt(EfronMorris$r/45))
s2data = rep(1/(4*45),18)
t2lik = function(t2) {
    t2s2 = t2 + s2data
    m = sum(ydata/t2s2) / sum(1/t2s2)
    prod(1/sqrt(2*pi*t2s2)) *
    sqrt(2*pi*(1/sum(1/t2s2))) *
    exp(-sum((ydata-m)^2/t2s2)/2)
}
vt2lik = Vectorize(t2lik)
f = function(t2) sqrt(sum(1/(t2+s2data)^2))
zt2 = function(t2) integrate(Vectorize(f), 0, t2)$value
x = seq(0.05,5,0.05)
t2seq = c(0, sapply(x, function(z) uniroot(function(t2) zt2(t2) - z, c(0,500))$root))
y = vt2lik(t2seq)
ymax = max(y)
plot(c(0,x), y, type="l", lwd=2, ylim=c(0,ymax*1.01),
     xlab=expression(italic(tau)^2), ylab="", yaxs="i", axes=FALSE)
t = c(0,0.001,0.002,0.005,0.01,0.02,0.05,0.1,0.2,0.5)
axis(1, sapply(t,zt2), t)

同じ問題を Stan で扱った例が Bob Carpenter による Hierarchical Partial Pooling for Repeated Binary Trials，およびそれに基づいた rstanarm パッケージによる Hierarchical Partial Pooling for Repeated Binary Trials にある。