2025年からの大学入学共通テストで出題される予定の「情報I」のサンプル問題が2021年3月24日に大学入試センターから公開された(これは大学入試センターが以前に作成して情報処理学会が公開した「情報」試作問題(検討用イメージ)より新しいものである)。ここでは,この新しいサンプル問題の,データを扱う第3問の問2について,細かい指摘をしておく。
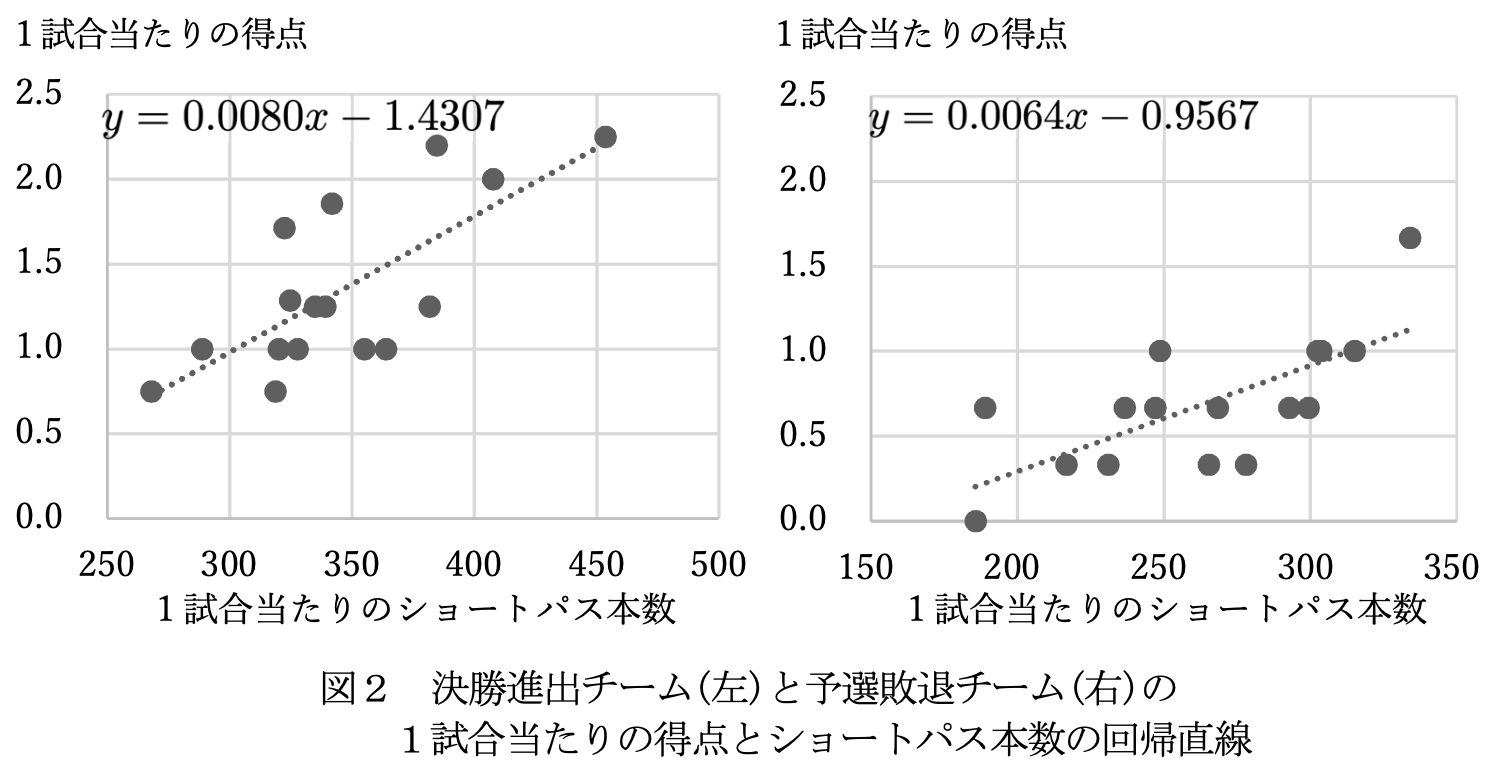
次の二つのデータと回帰直線を見て計算する問題である。回帰係数はあらかじめ計算されていて,その意味を読み取る問題である。

この計算結果について,問題では「鈴木さんは,グラフからは傾きに大きな差が見られないこの二つの回帰直線について,実際に計算してみると差を見つけられることが実感できた。」と結論づけている。
本当に「差を見つけられること」ができたのか?
WebPlotDigitizer を使って,図から数値を読み取ってみる。
左側:
x,y 267.469,0.750 287.878,0.998 318.043,0.752 319.442,1.000 321.850,1.713 324.063,1.289 326.974,1.000 333.753,1.253 338.774,1.254 341.198,1.858 354.593,0.996 363.559,1.002 381.458,1.250 384.191,2.201 407.174,2.005 453.050,2.255
R コード:
df1 = read.csv("df1.csv")
summary(lm(y ~ x, data=df1))
結果:
Call:
lm(formula = y ~ x, data = df1)
Residuals:
Min 1Q Median 3Q Max
-0.49395 -0.24590 0.01158 0.12252 0.55234
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -1.426660 0.694234 -2.055 0.05903 .
x 0.008039 0.001995 4.030 0.00124 **
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.3511 on 14 degrees of freedom
Multiple R-squared: 0.537, Adjusted R-squared: 0.504
F-statistic: 16.24 on 1 and 14 DF, p-value: 0.001241
右側:
x,y 185.580,0.000 189.100,0.667 216.608,0.333 230.956,0.333 236.733,0.667 247.063,0.667 249.110,1.000 265.389,0.333 268.584,0.667 278.014,0.333 292.974,0.667 299.573,0.667 302.481,1.000 303.629,1.000 315.107,1.000 334.122,1.667
結果:
Call:
lm(formula = y ~ x, data = df2)
Residuals:
Min 1Q Median 3Q Max
-0.44546 -0.20270 -0.03121 0.09767 0.53864
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -0.955304 0.455039 -2.099 0.05439 .
x 0.006236 0.001705 3.658 0.00259 **
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.2916 on 14 degrees of freedom
Multiple R-squared: 0.4886, Adjusted R-squared: 0.4521
F-statistic: 13.38 on 1 and 14 DF, p-value: 0.002585
要は,それぞれの傾きの標準誤差が 0.0020,0.0017 といった値であるのに対して,傾きの差は 0.0016 しかない。つまり,統計的にまったく有意ではない。
差を実感してもらっては困る,ということだ(受験生はわからなくていいけれども,出題者には差を実感してほしくない,という意味)。