$i = 1, \ldots, n$ について,誤差を含むデータ $y_i$ と,誤差を含まないデータ(いくつあってもいいがここでは $x_i$)が与えられている。$y_i$ が,いくつかのパラメータ(ここでは $a$,$b$)についての1次式(ここでは $ax_i + b$)で近似的に与えられ,誤差は互いに独立で分散 $\sigma_i^2$ の正規分布に従うとする:
\[ y_i \sim N(ax_i + b, \sigma_i^2) \]このようなパラメータ $a$,$b$ の値と誤差を推定したい。あるいはベイズ風に $a$,$b$ の事後分布を求めたい。
よくある問題設定では,誤差分散はすべて等しい($\sigma_1^2 = \sigma_2^2 = \ldots = \sigma_n^2 = s^2$)あるいは与えられた重みベクトルに反比例する($\sigma_i^2 = s^2/w_i$)と仮定し,データから $s^2$ を推定する。一方,物理学では各データ点の誤差 $\sigma_i^2$ が与えられていることが多い。データのプロットで $\pm \sigma_i$ がエラーバーとして描かれているのをよく目にする(下の図参照)。物理以外でも誤差が与えられることはよくある。物理以外では95%信頼区間(ほぼ $\pm 1.96\sigma_i$)のエラーバーを描くことが多い。
尤度は
\[ p(a,b) = \prod_{i=1}^n \frac{1}{\sqrt{2\pi\sigma_i^2}} \exp \left( - \frac{(ax_i + b - y_i)^2}{2\sigma_i^2} \right) \]である。これを $a$ だけの関数と見ると,正規分布の密度関数 $\exp (-(a - a_0)^2 / (2 \sigma_a^2))$ の形をしているので,$a^2$ の係数を比較すれば,分散 $\sigma_a^2 = 1 / \sum (x_i^2/\sigma_i^2)$ が導かれる。しかしこれは $x_i \to x_i + c$ のような変換について不変ではない(後述のように $\sigma_a^2$ を最大にする $c$ を求めることはできる)。同様に,$b$ だけの関数と見ると,分散 $\sigma_b^2 = 1 / \sum ( 1 / \sigma_i^2)$ が導かれる。
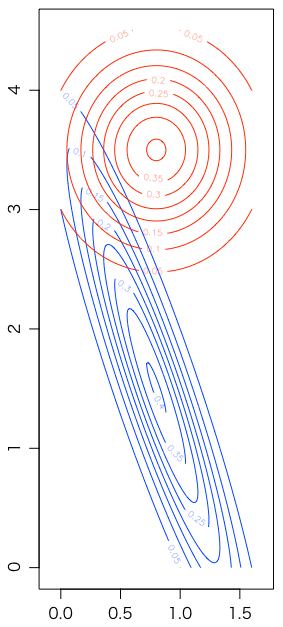
これがどういうことかは,具体例を見るほうがわかりやすいかもしれない。拙著『Rで楽しむ統計』第9章の最初の例 $x = (1,2,3,4)$,$y = (2,3,5,4)$ の尤度(係数を除く)が次の青い等高線である。赤い等高線は $x = (-1.5,-0.5,0.5,1.5)$ にシフトした場合である。横軸が $a$,縦軸が $b$ である:

foo = function(a,b) exp(-0.5*sum((a*x+b-y)^2))
x = 1:4; y = c(2,3,5,4)
m1 = outer((0:160)/100, (0:450)/100, Vectorize(function(a,b) foo(a,b)))
x = (1:4)-2.5; y = c(2,3,5,4)
m2 = outer((0:160)/100, (0:450)/100, Vectorize(function(a,b) foo(a,b)))
contour((0:160)/100, (0:450)/100, m1, asp=1, col="#0041ff")
contour((0:160)/100, (0:450)/100, m2, asp=1, col="#ff2800", add=TRUE)
対数尤度は
\[ \log p(a,b) = - \frac{1}{2} \sum_{i=1}^n \left( \frac{ax_i + b - y_i}{\sigma_i} \right)^2 + \text{const.} \]である。したがって $a$,$b$ の最尤推定値は
\[ \chi^2 = \sum_{i=1}^n \left( \frac{ax_i + b - y_i}{\sigma_i} \right)^2 \]を最小化して求められる。この最小化を物理ではしばしば「$\chi^2$(カイ2乗)最小化」と呼ぶ。最小化された値と自由度 $n-2$ の $\chi^2$ 分布を比べて,あてはまりが悪ければモデルを疑い,逆に良すぎれば誤差 $\sigma_i^2$ の評価を疑う。
実際の最小化は,上の $\chi^2$ の式を $a$ および $b$ で微分したものを 0 と置いて得られる連立方程式を解けばよい。これは自前でプログラムを書かなくても,Rの lm() を使えばよい。ただし lm() は上に述べた「よくある問題設定」に従っているので,デフォルトでは $\sigma_i^2 = s^2$ はすべて等しいとし,オプション weights=... で重みベクトルを与えれば $\sigma_i^2 = s^2/w_i$ として,$s^2$ をデータから推定する。したがって,$a$,$b$ を求めるだけなら lm() をオプション weights=$1/\sigma_i^2$ で使えばよい。lm() の具体的な使い方は拙著『Rで楽しむ統計』第9章を参照されたい。
lm() で求める誤差分散は,$s^2$ をデータから推定することを除き,基本的に対数尤度を二つのパラメータで微分したヘッセ行列の逆行列である。このあたりは,最近は高校で行列を習わないので,ここでは省略し,ベイズ統計の計算のほうを紹介する。結果は同じである。
拙著『Rで楽しむベイズ統計入門』7.5節の方法は,事前分布を $a$,$b$,$\log s^2$ について一様として事後分布を求める。$\log s^2$ で積分して $s$ を消せば,古典的な最小2乗法と形式的に同じ結果が得られる。ここでも $\sigma_i^2$ が与えられた場合の計算は扱わなかった。以下で扱うのは $\sigma_i^2$ が与えられた場合である。
事前分布は $a$,$b$ について一様と仮定するので,さきほどの尤度 $p(a,b)$ は(定数倍を除いて)$a$,$b$ の事後分布でもある。この式を,$b$ を固定して $a$ だけについて見れば,その分布は分散 $1 / \sum (x_i^2/\sigma_i^2)$ の正規分布である。また,$a$ を固定して $b$ だけについて見れば,その分布は分散 $1 / \sum ( 1 / \sigma_i^2)$ の正規分布である。ここまでは最尤法で求めた $a$,$b$ の誤差分布と同じである。しかしこの $a$ の分散は $x_i \to x_i + c$ のような変換について不変ではない。$b$ を固定しているので,これは当然である。
ベイズ統計の枠内で,より適切な $a$ の誤差分布は,事後分布 $p(a,b)$ を $b$ について積分した分布(周辺分布)$p(a) = \int p(a,b) db$ である。以下ではこれを求めよう。
\[ w_i = \frac{1}{\sigma_i^2} \]と置き,$a$,$b$ を含まない項を省略して,
\[ -2 \log p(a,b) = \sum_{i=1}^n w_i (ax_i + b - y_i)^2 \]と書く。$b$ について平方完成すると,
\begin{align} \sum w_i(ax_i+b-y_i)^2 &= b^2\sum w_i + 2b\sum w_i(ax_i-y_i) + \sum w_i(ax_i-y_i)^2 \\ &= \sum w_i \left( b^2 + 2b\frac{\sum w_i(ax_i-y_i)}{\sum w_i} + \left ( \frac{\sum w_i(ax_i-y_i)}{\sum w_i} \right)^2 \right) \\ & \quad - \frac{(\sum w_i(ax_i-y_i))^2}{\sum w_i} + \sum w_i(ax_i-y_i)^2 \\ &= \sum w_i \left( b + \frac{\sum w_i(ax_i-y_i)}{\sum w_i} \right)^2 + A \end{align}したがって,
\[ p(a) = \int p(a,b) db \propto \int \exp \left(- \frac{1}{2} \sum w_i (b + \cdots)^2 \right) db \cdot \exp (-A/2) \propto \exp(-A/2) \]となるので $A$ の部分だけ評価すればよい。特に,$a$ の分散を調べるには $a^2$ に比例する部分だけ見ればよい:
\[ A = a^2 \left( \sum w_i x_i^2 - \frac{(\sum w_i x_i)^2}{\sum w_i} \right) + O(a) \]この大きい括弧の部分は「2乗の(重み付き)平均引く(重み付き)平均の2乗」になっているが,これは(重み付き)分散にほかならない:
\begin{align} \sum w_i \left( x_i - \frac{\sum w_i x_i}{\sum w_i} \right)^2 &= \sum w_i x_i^2 - 2 \sum w_i x_i \frac{\sum w_i x_i}{\sum w_i} + \sum w_i \left( \frac{\sum w_i x_i}{\sum w_i} \right)^2 \\ &= \sum w_i x_i^2 - \frac{(\sum w_i x_i)^2}{\sum w_i} \end{align}したがって,$a$ の分散 $\sigma_a^2$ は
\[ \frac{1}{\sigma_a^2} = \sum w_i \left( x_i - \frac{\sum w_i x_i}{\sum w_i} \right)^2 = \sum \frac{1}{\sigma_i^2} \left( x_i - \frac{\sum x_i/\sigma_i^2}{\sum 1/\sigma_i^2} \right)^2 \]で求められる。
なお,最尤法の枠内で求められる $b$ を固定した場合の $a$ の分散の逆数は $\sum w_i x_i^2$ であったが,これは $x_i \to x_i + c$ で不変でなかった。そこで $\sum w_i (x_i + c)^2$ を最小にする $c$ を求めれば,上と同じ結果を得る。
同様に,$b$ の誤差を求めるために $a$ について平方完成すると,
\begin{align} & \sum w_i(ax_i+b-y_i)^2 \\ &= \left( \sum w_i x_i^2 \right) \left( a + \frac{\sum w_i x_i (b - y_i)}{\sum w_i x_i^2} \right)^2 + b^2 \left( \sum w_i - \frac{(\sum w_i x_i)^2}{\sum w_i x_i^2} \right) + O(b) \end{align}この $b^2$ の係数が $b$ の分散の逆数である:
\[ \frac{1}{\sigma_b^2} = \sum w_i - \frac{(\sum w_i x_i)^2}{\sum w_i x_i^2} = \sum w_i \left( x_i - \frac{\sum w_i x_i}{\sum w_i} \right)^2 \cdot \frac{\sum w_i}{\sum w_i x_i^2} \]つまり $b$ の分散は $a$ の分散に $x_i$ の2乗の(重み付き)平均をかけたものである:
\[ \sigma_b^2 = \frac{\sum w_i x_i^2}{\sum w_i} \sigma_a^2 \]これは $x_i \to x_i + c$ で不変でない。
例として,『Rで楽しむ統計』第9.3節の「第五の力」(Fischbach たち,1986年)のデータを調べよう。
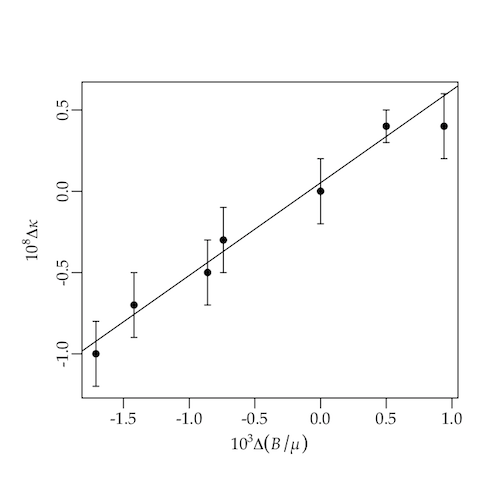
x = c(0.94, 0.50, 0.00, -0.74, -0.86, -1.42, -1.71)
y = c(0.4, 0.4, 0.0, -0.3, -0.5, -0.7, -1.0)
e = c(0.2, 0.1, 0.2, 0.2, 0.2, 0.2, 0.2)
r = lm(y ~ x, weights=1/e^2)
summary(r)
b = r$coefficients[1]
a = r$coefficients[2]
chi2 = sum(((a * x + b - y) / e)^2) # 1.795245
pchisq(chi2, 5) # 0.1233112
xbar = sum(x / e^2) / sum(1 / e^2)
sa2 = 1 / sum(((x - xbar) / e)^2)
sqrt(sa2) # 0.07165334
sb2 = sa2 * sum(x^2 / e^2) / sum(1 / e^2)
sqrt(sb2) # 0.06453298
lm() で求めた $a$ の標準誤差は 0.04 ほどだが,上の方法で求めれば $\sigma_a = 0.07$ ほどになる。
例えば上の問題で
r = lm(y ~ x, weights=1/e^2)
summary(r)
とすると,次のように表示される(朱書きした部分に注目):
Call:
lm(formula = y ~ x, weights = 1/e^2)
Weighted Residuals:
1 2 3 4 5 6 7
-0.9404 0.6282 -0.2603 0.3495 -0.3084 0.2882 -0.3850
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.05207 0.03867 1.347 0.236
x 0.57022 0.04294 13.281 4.33e-05 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.5992 on 5 degrees of freedom
Multiple R-squared: 0.9724, Adjusted R-squared: 0.9669
F-statistic: 176.4 on 1 and 5 DF, p-value: 4.327e-05
この Coefficients の Std. Error に Residual standard error の逆数をかければ,$\sigma_i^2$ の与えられた場合の係数の誤差が求められるのだ。あるいは次のように打ち込んでもよい:
sr = summary(r)
sr$coefficients[,2] / sr$sigma
これで 0.06453298 と 0.07165334 が得られる。この方法なら,係数が増えても大丈夫である。