Simon_Sin さんのこのツイートが RT されてきた:
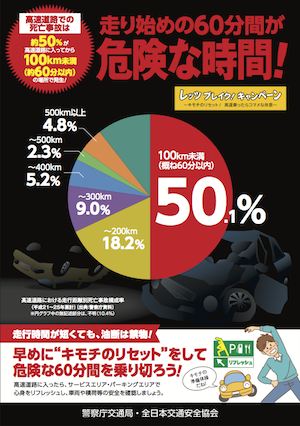
「高速道路走行は走り始めの60分が危険」というポスターをみて違和感を覚えたのでちょっと調べたが高速道路を走る車の平均走行距離は54km、60分以下なので走り始めの60分が危険なのではなく「高速道路を60分以上走行する車は少ない(ので事故件数も少ない)」ということではないか。騙されるとこだったぜ pic.twitter.com/PzXgJHnQW3
— Simon_Sin (@Simon_Sin) 2018年8月8日

このポスター(右に再掲)は,警察庁交通局・全日本交通安全協会のもので,2014年(平成26年)11月20日の公安委員会報告案件 広報資料(PDF)の3ページ目や,一般財団法人 全日本交通安全協会のこちら(PDF)にある。前者の1ページ目には,同じデータを帯グラフで表したものも載っている。
同じグラフが,2017年4月26日のNHK「ガッテン!」大型連休の前に!交通事故から家族を守りたいSPでも使われ,そのときもツイッター上で問題点が指摘された。まとめがNHKのガッテンがまたもやトリッキーなデータの使い方をしているにある。
要は,死亡事故を起こした人の50.1%が走行距離100km未満(概ね60分以内)であるのは確かだが,死亡事故を起こしていない人の何%が100km走行したかがわからない限り,「100km未満」が危険かどうかわからないということである。
極端な例で示せば,「死亡事故を起こした人の90%が朝ごはんを食べていた」(架空のデータだが)。
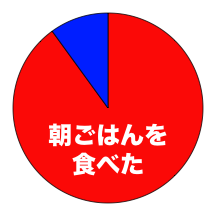
これで「朝ごはんは危険!」と言えるであろうか。
同様な話は何度となく聞いた覚えがある。例えば:
がんで死ぬ人の90%は朝ご飯を食べてます。(推測)RT @motoken_tw: 短絡的な人がよくやる因果関係の誤解かな。RT @touyoui: 岡山大学付属病院のインターンの学生が調べてみると、80%がガンの三大療法(手術、抗がん剤、放射線治療)で死んでいた。
— buvery (@buvery) 2013年2月16日
ちなみに,ネットで流れている「岡山大学付属病院のインターンの学生が調べてみると、80%がガンの三大療法(手術、抗がん剤、放射線治療)で死んでいた」の続きは「その発見を論文にしようとしたが、握りつぶされた」である。
結論:「○○した人の何%は・・・」と言われたら眉に唾をつけよう。
類例:「○○癌の90%を発見する方法が開発された」だけでは情報不足。病気を病気だと判断できる確率を「感度」(sensitivity)という。病気でない人を病気でないと判断できる確率を「特異度」(specificity)という。この両方が示されない限り,判断できない。
90%が朝ごはんを食べた円グラフは次のようにしてRで描いた:
x = c(90,10)
c = c("#ff2800", "#0041ff")
pie(x, clockwise=TRUE, radius=0.95, labels=NA, col=c)
text(0, -0.4, "朝ごはんを\n食べた", cex=2, col="white", family="HiraKakuStdN-W8")

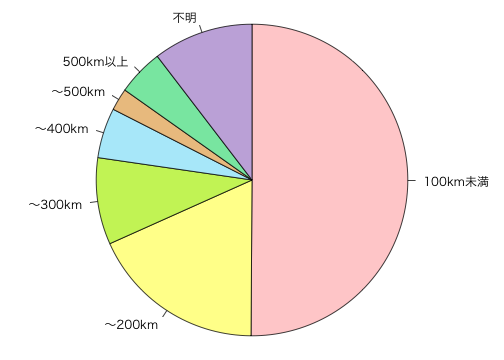
死亡事故を起こした人の走行距離の円グラフは次のようになる。色はカラーユニバーサルデザイン推奨配色セットのベースカラーを用いた(統計グラフの色参照):
x = c(50.1, 18.2, 9.0, 5.2, 2.3, 4.8, 10.4)
l = c("100km未満", "〜200km", "〜300km", "〜400km", "〜500km", "500km以上", "不明")
c = c("#ffd1d1", "#ffff99", "#cbf266", "#b4ebfa", "#edc58f", "#87e7b0", "#c7b2de")
pie(x, clockwise=TRUE, radius=0.95, labels=l, col=c)
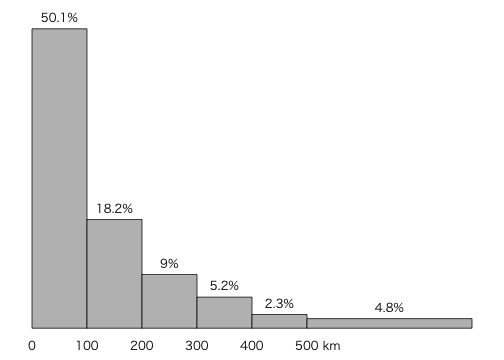
同じものをヒストグラムで描いてみよう:
t = c(0, 100, 200, 300, 400, 500, 800)
dt = diff(t)
x = c(50.1, 18.2, 9.0, 5.2, 2.3, 4.8)
barplot(x/dt, dt, space=0, axes=FALSE)
axis(1, c(t[1:6],550), c(t[1:6],"km"), lwd=0, mgp=c(1,0.5,0))
text(t[1:6]+dt/2, x/dt, paste0(x,"%"), pos=3, xpd=TRUE)
mtext("km", 1, 0.5, at=545)
各区間の代表値を 50, 150, 250, 350, 450, 550 とすると,事故の起こるまでの平均走行距離は
sum((t[1:6]+50) * x) / sum(x)[1] 144.8661
これは Simon_Sin さんの挙げておられる平均走行距離よりずっと長い。ということは・・・