文科省が全国学力・学習状況調査(全国学力テスト)のパブリックユースデータ(擬似データ)を公開した。これをRで読み込んで中を調べる方法を解説する。
ここでは生徒データ(Excel:3126KB)つまり中学生(中3)のデータを使う。まずはダウンロードして,Excelで開いてみよう。このような,1行目に変数名,2行目以降に値が並び,セル結合をしていない素直な長方形データは,Rで簡単に扱える。
昔なら,いったんCSVファイルに変換してからRで読み込むところだが,CSVファイルの文字コードによってはRで文字化けが起こったりするので,初心者向きでなかった。今は,RでExcelファイルをそのまま読み込むほうが簡単である。
Excelファイルを読み込む操作は,RStudioならマウスで簡単にできる。右上のペインで「Import Dataset」→「From Excel…」をクリックする(初回使用時にはライブラリのインストールが始まり,しばらく待たされる)。「Browse…」ボタンを押し,ダウンロードしたファイル 1404609_2_1.xlsx を探し,「Open」を押す。データのプレビュー画面が現れる。左下の「Import Options:」で,「Name:」のところ(データの名前)がファイル名から自動生成された「X1404609_2_1」になっている。このままでもよいが,後でわかりやすいように,ここではこれを「seito」に直し,念のためマウスで別の入力欄をクリックする(あるいは Tab キーまたは Enter キーを打つ)。プレビューが再生成されたことを確認してから,右下の「Import」を押す。
もし上で「ここではこれを「seito」に直し」の部分を忘れたなら,後で seito = X1404609_2_1 と打ち込めば,変数名が seito になる。
同じことを素のRで行うには,次のように打ち込む:
library(readxl)# これがエラーになるなら install.packages("readxl") するseito = read_excel("1404609_2_1.xlsx")# Excelファイルの保存場所に注意
これで seito という変数に生徒データが読み込まれた。
seito# 中を見てみる# A tibble: 2,000 x 430実施年 地域規模 解答用紙番号 性別 生徒質問紙種別 正答数_国A 正答数_国B<dbl> <dbl> <dbl> <dbl> <lgl> <dbl> <dbl>1 2015 3 1 2 NA 27 72 2015 1 2 2 NA 26 43 2015 1 3 2 NA 27 74 2015 2 4 1 NA 22 75 2015 1 5 2 NA 27 86 2015 2 6 2 NA 27 37 2015 4 7 2 NA 19 78 2015 1 8 1 NA 23 69 2015 3 9 1 NA 20 510 2015 3 10 1 NA 32 9# ... with 1,990 more rows, and 423 more variables: 正答数_数A <dbl>,# 正答数_数B <dbl>, 正答数_理 <dbl>, 正答数_理A <dbl>, 正答数_理B <dbl>,# 正答率_国A <dbl>, 正答率_国B <dbl>, 正答率_数A <dbl>, 正答率_数B <dbl>,# 正答率_理 <dbl>, 正答率_理A <dbl>, 正答率_理B <dbl>, 学力層_国A <dbl>,# 学力層_国B <dbl>, 学力層_数A <dbl>, 学力層_数B <dbl>, 学力層_理科 <dbl>,# 学力層_理科A <dbl>, 学力層_理科B <dbl>, 正答数_国A_領域1 <dbl>, …
データ行列の行数・列数を調べる:
dim(seito)[1] 2000 430
変数名一覧を列挙する:
names(seito)[1] "実施年" "地域規模" "解答用紙番号"[4] "性別" "生徒質問紙種別" "正答数_国A"[7] "正答数_国B" "正答数_数A" "正答数_数B"[10] "正答数_理" "正答数_理A" "正答数_理B"[13] "正答率_国A" "正答率_国B" "正答率_数A"[16] "正答率_数B" "正答率_理" "正答率_理A"[19] "正答率_理B" "学力層_国A" "学力層_国B"(以下略)
1〜19番の変数のサマリー(最小値,第1四分位数,中央値,平均値,第3四分位数,最大値)を出力する:
summary(seito[,1:19])
実施年 地域規模 解答用紙番号 性別 生徒質問紙種別
Min. :2015 Min. :1.00 Min. : 1.0 Min. :1.0 Mode:logical
1st Qu.:2015 1st Qu.:2.00 1st Qu.: 500.8 1st Qu.:1.0 NA's:2000
Median :2015 Median :3.00 Median :1000.5 Median :1.5
Mean :2015 Mean :2.47 Mean :1000.5 Mean :1.5
3rd Qu.:2015 3rd Qu.:3.00 3rd Qu.:1500.2 3rd Qu.:2.0
Max. :2015 Max. :4.00 Max. :2000.0 Max. :2.0
正答数_国A 正答数_国B 正答数_数A 正答数_数B
Min. : 7.00 Min. :0.000 Min. : 3.00 Min. : 0.000
1st Qu.:22.00 1st Qu.:5.000 1st Qu.:18.75 1st Qu.: 4.000
Median :25.00 Median :6.000 Median :23.00 Median : 6.000
Mean :24.79 Mean :5.888 Mean :22.95 Mean : 6.505
3rd Qu.:28.00 3rd Qu.:7.000 3rd Qu.:28.00 3rd Qu.: 9.000
Max. :33.00 Max. :9.000 Max. :36.00 Max. :15.000
(以下略)
詳しくはデータレイアウト(PDF:784KB)にあるが,実施年はすべて2015,地域規模は1:大都市,2:中核市,3:その他の市,4:町村,性別は1:男子,2:女子,0:不明,生徒質問紙種別はすべて欠測値(NA)である。その次からが正答数と,100点満点に換算した正答率が続く。
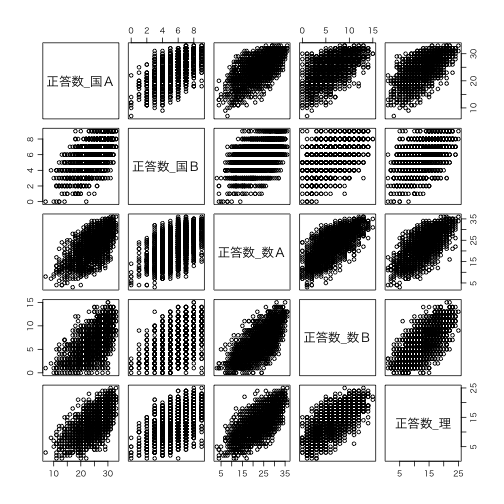
国語A,国語B,数学A,数学B,理科の5科目それぞれ45分で答える。Aは基本,Bは応用である。それぞれの満点はデータの最大値に等しい。データでは理科以外に理科A,理科Bがあるが,便宜上二つに分けたようで,基本・応用という区別ではなさそうである。5科目を単純にプロットしてみる:
plot(seito[,6:10])

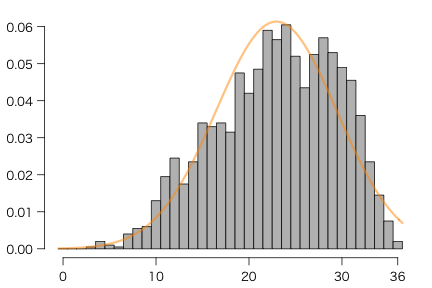
数学Aの正答数分布のヒストグラムを描いてみよう(グラフの例:ヒストグラム参照)。seito の8番目の変数である数学Aの正答数をベクトル(数値の列)として取り出すには seito$正答数_数A または seito[[8]] とする。全角・半角を区別するので seito$正答数_数A ではエラーになる。また,seito[,8] でもいいような気がするが,read_excel() の出力するtibbleというデータ構造は,seito[,8] では1列だけのtibbleとなって,ベクトル(数値の列)を要求する場面ではエラーになる。
hist(seito[[8]], breaks=0:37, right=FALSE)
もうちょっとがんばって綺麗にする:
par(mar=c(2,3,1,1)+0.1) # 下・左・上・右マージン(デフォルト: c(5,4,4,2)+0.1)
par(mgp=c(2,0.8,0)) # 軸マージン(デフォルト: c(3,1,0))
par(las=1) # 文字は水平に
hist(seito[[8]], breaks=0:37, right=FALSE,
main="", freq=FALSE, xlab="", ylab="", xaxt="n")
t = c(0, 10, 20, 30, 36) # 目盛位置
axis(1, t+0.5, t) # 位置を0.5ずらす
ついでに,平均・標準偏差の等しい正規分布の密度関数を重ね書きしてみる:
curve(dnorm(x, mean(seito[[8]])+0.5, sd(seito[[8]])), add=TRUE, col="#ff990080", lwd=3)
国語Aと国語Bの正答率の平均,数学Aと数学Bの正答率の平均,5科目の正答率の平均を求めて,seito に追加する:
seito$正答率_国 = (seito$正答率_国A + seito$正答率_国B) / 2 # あるいは rowMeans(seito[,13:14]
seito$正答率_数 = (seito$正答率_数A + seito$正答率_数B) / 2 # あるいは rowMeans(seito[,15:16]
seito$正答率 = rowMeans(seito[,13:17])
これらの散布図(相関図)を描く:
plot(seito$正答率_国, seito$正答率_数)
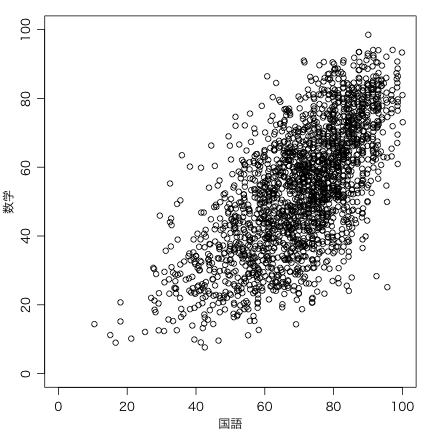
もうちょっとがんばってきれいにする。重なりを避けるため,ほんの少し(±0.2)ジッター(ぶれ)を付けてみた:
par(mgp=c(2,0.8,0)) # 軸マージン(デフォルト: c(3,1,0))
plot(jitter(seito$正答率_国,amount=0.2), jitter(seito$正答率_数,amount=0.2),
xlim=c(0,100), ylim=c(0,100), xlab="国語", ylab="数学")
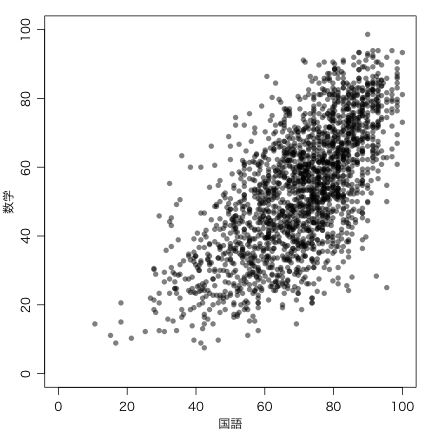
半透明の黒丸を使う手もある:
plot(seito$正答率_国, seito$正答率_数, pch=16, col="#00000080",
xlim=c(0,100), ylim=c(0,100), xlab="国語", ylab="数学")
例えば男女を別の色にすることによって情報量が増す:
par(mar=c(3,3,1,1)+0.1) # 下・左・上・右マージン(デフォルト: c(5,4,4,2)+0.1)
par(mgp=c(2,0.8,0)) # 軸マージン(デフォルト: c(3,1,0))
cols = c("#0041ff80","#ff280080")
plot(seito$正答率_国, seito$正答率_数, pch=16, col=cols[seito$性別],
xlim=c(0,100), ylim=c(0,100), xlab="国語", ylab="数学")
legend("topleft", c("男","女"), pch=16, col=cols)
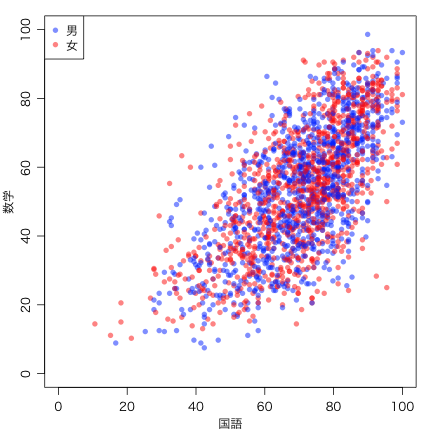
相関係数は cor() または cor.test() で求める:
cor.test(seito$正答率_国, seito$正答率_数)Pearson's product-moment correlationdata: seito$正答率_国 and seito$正答率_数t = 39.736, df = 1998, p-value < 2.2e-16alternative hypothesis: true correlation is not equal to 095 percent confidence interval:0.6391802 0.6881876sample estimates:cor0.6643974
数学は男子のほうができるのであろうか?
mean(seito$正答率_数[seito$性別 == 1])[1] 53.6175mean(seito$正答率_数[seito$性別 == 2])[1] 53.49639
次のように書くこともできる:
with(seito, tapply(正答率_数, 性別, mean))1 253.61750 53.49639
男子(1)のほうが女子(2)より多少平均点が高いように見える。箱ひげ図で比べてみよう。
boxplot(正答率_数 ~ 性別, data=seito, ylim=c(0,100), names=c("男","女"))
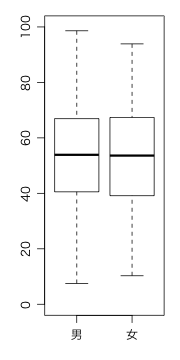
差はなさそうである。念のため t 検定をしてみる:
t.test(seito$正答率_数[seito$性別==1], seito$正答率_数[seito$性別==2])
または同じことであるが次のようにするほうが楽である:
t.test(正答率_数 ~ 性別, data=seito)
結果は次のようになる:
Welch Two Sample t-test
data: 正答率_数 by 性別
t = 0.14809, df = 1996.7, p-value = 0.8823
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-1.482746 1.724968
sample estimates:
mean in group 1 mean in group 2
53.61750 53.49639
同様に,5科目平均正答率が地域規模と関係しているか,箱ひげ図と分散分析で調べてみる:
boxplot(正答率 ~ 地域規模, data=seito)oneway.test(正答率 ~ 地域規模, data=seito)One-way analysis of means (not assuming equal variances)data: 正答率 and 地域規模F = 0.94629, num df = 3.00, denom df = 629.17, p-value = 0.4178
図は略す。有意な差はない。
「生徒質問紙回答_001」は平成27年度全国学力・学習状況調査の調査問題・正答例・解説資料についての「生徒質問紙」によれば「朝食を毎日食べている」で,1:している,2:どちらかといえば,している,3:あまりしていない,4:全くしていないの4択である。それぞれの数は次のようにして求められる:
table(seito$生徒質問紙回答_001)1 2 31332 626 42
boxplot() と oneway.test() で調べてみるとよい。