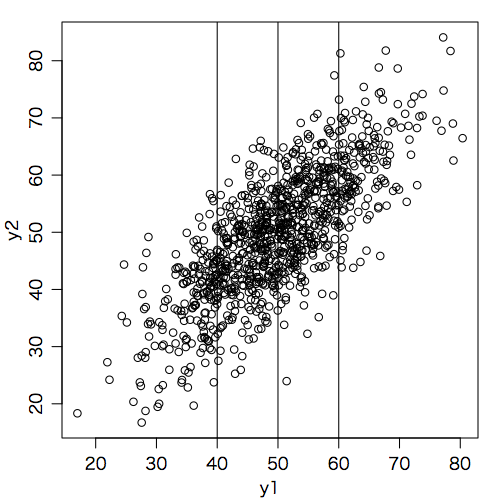
星野崇宏『調査観察データの統計科学』(岩波,2009)をパラパラ見ていたら,p.32に「入試得点による選抜と欠測」というよく見る図があった。y1 が入試得点,y2 が入学後の成績で,本では60点以上が合格となっていた。下の図は線引きを40点,50点,60点と3箇所にしたものである。

y1 = rnorm(1000, 50, 10)
y2 = rnorm(1000, 10 + 0.8 * y1, 7)
plot(y1, y2)
abline(v=c(40,50,60))
入学後の成績は合格者についてしか観測できないので,不合格者は欠測になり,相関係数は選択バイアスを受けることになるが,回帰係数は影響を受けないという,言われてみれば至極当然のことが書かれていた。
シミュレーションで確かめてみよう。
f = function(th) {
y1 = rnorm(1000, 50, 10)
y2 = rnorm(1000, 10 + 0.8 * y1, 7)
y2 = y2[y1 >= th]
y1 = y1[y1 >= th]
r = cor(y1, y2)
b = lm(y2 ~ y1)$coefficients[2]
c(r, b)
}
a1 = replicate(1000, f(0))
a2 = replicate(1000, f(40))
a3 = replicate(1000, f(50))
a4 = replicate(1000, f(60))
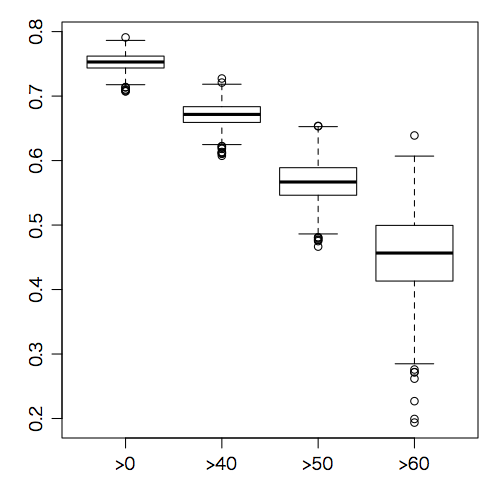
boxplot(a1[1,], a2[1,], a3[1,], a4[1,], names=c(">0",">40",">50",">60")) # 相関係数
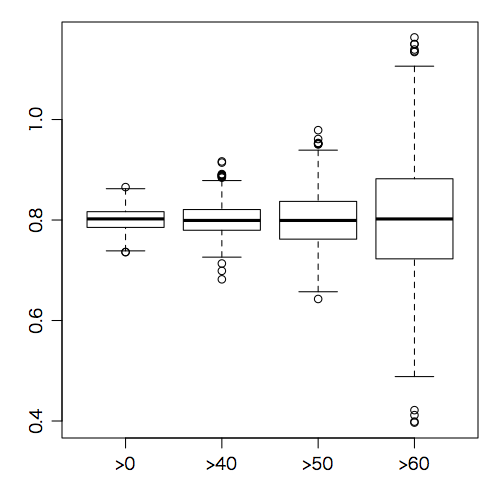
boxplot(a1[2,], a2[2,], a3[2,], a4[2,], names=c(">0",">40",">50",">60")) # 回帰係数
全員合格,40点以上合格,50点以上合格,60点以上合格の場合の相関係数の箱ひげ図は次のようになる:
一方,回帰係数(傾き)の箱ひげ図は次のようになる: