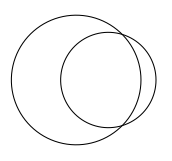
正しい比率で描くとこんなもんでしょうか pic.twitter.com/XpsyaulAvB
— Haruhiko Okumura (@h_okumura) 2017年7月25日
このような正しい面積比の円を描いてみよう。
2円の中心を $\mathrm{O}_1$, $\mathrm{O}_2$ とし,2円の交点を $\mathrm{A}$, $\mathrm{B}$ とする。それぞれの半径は $r_1 = \mathrm{O_1A}$, $r_2 = \mathrm{O_2A}$ である。中心間の距離を $d = \mathrm{O_1O_2}$ とする。さらに $\theta_1 = \angle\mathrm{AO_1O_2}$, $\theta_2 = \angle\mathrm{AO_2O_1}$ とする。余弦定理より
\[ \cos\theta_1 = \frac{r_1^2 + d^2 - r_2^2}{2r_1d}, \qquad \cos\theta_2 = \frac{r_2^2 + d^2 - r_1^2}{2r_2d} \]となる。直線 $\mathrm{AB}$ より左の面積は
\[ r_1^2(\pi - \theta_1 + \sin\theta_1 \cos\theta_1) \]であり,直線 $\mathrm{AB}$ より右の面積も同様である。これらの和が全体の面積である(追記:acos() の定義域を微妙に外れる場合にエラーが出ないようにしました。@gnutar 先生ありがとうございます):
area = function(r1,r2,d) {
theta1 = acos(min(max((r1^2 + d^2 - r2^2) / (2 * r1 * d), -1), 1))
theta2 = acos(min(max((r2^2 + d^2 - r1^2) / (2 * r2 * d), -1), 1))
r1^2 * (pi - theta1 + sin(theta1) * cos(theta1)) + r2^2 * (pi - theta2 + sin(theta2) * cos(theta2))
}
描きたい図形は,2円の面積がそれぞれ 85,46 で,共通部分が 39 であるので,
r1 = sqrt(85/pi)
r2 = sqrt(46/pi)
a = 85+46-39
d = uniroot(function(d) area(r1,r2,d) - a, c(abs(r1-r2),r1+r2))$root
この結果は d = 2.581113 になる。したがって,
plot(NULL, xlim=c(-r1,d+r2), ylim=c(-r1,r1), axes=FALSE, asp=1, xlab="", ylab="")
theta = seq(0, 2*pi, length.out=100)
points(r1*cos(theta), r1*sin(theta), type="l")
points(r2*cos(theta)+d, r2*sin(theta), type="l")

ちょっとだけ追記。上の記事の元になったのは【LINE】〈調査報告〉インターネットの利用環境 定点調査(2017年上期)にあるベン図みたいなグラフで,スマホ利用者85%,PC利用者46%,それらの重なりが39%であることを,重なった2円で表したものだが,面積ではなく半径が利用者数に比例するように描かれており,重なりも適当で,明らかにまずい。そこで,正しい面積比で描くための計算を示したのがこの記事である。計算は実際にはもうちょっと短くできるが,説明が簡単なようにした。ここにあるように,最初から円でなく帯グラフにすれば話は簡単である。なお,こちらのブログではPythonで描いてくださっている。