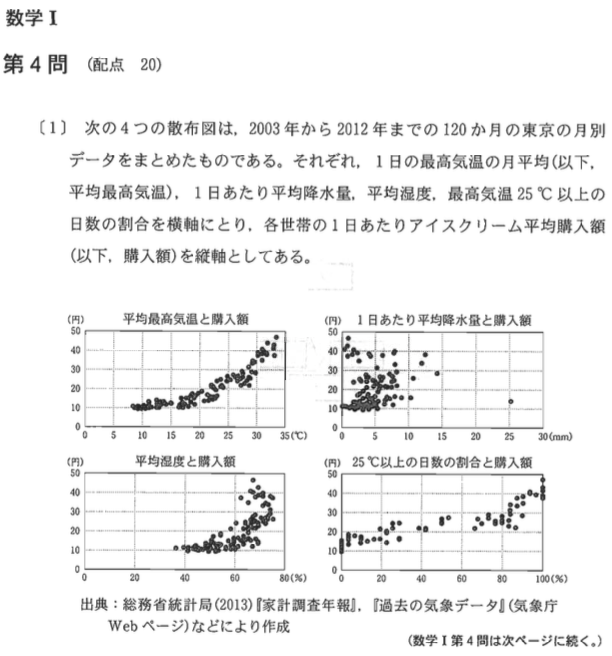
2016年1月17日の入試センター試験「数学①」の「数学I」(全問必答)の第4問および「数学I・数学A」の第2問(必答問題)で,2003〜2012年の120か月の各世帯の1日あたりアイスクリーム平均購入額と,東京の月別気象データの相関を調べる問題が出題された。

アイスクリーム平均購入額については,「総務省統計局(2013)『家計調査年報』」が出典と書かれているが,Googleで検索して出てきた家計調査年報(家計収支編)平成25年(2013年)を見てもどこにあるのかわからない。
そこで,e-Stat のキーワード検索で「アイスクリーム」を入れる。一覧から「家計調査」→「家計収支編」をクリック,左で「データベース」を選び「表題一覧表示」をクリック,「月次」があるのは上の三つだけなので,最新のもの(一番上)の「DB」を選ぶ。
「1/5 表章項目」で「選択」をクリック,「金額」しかないのでそれを選択し,「選択項目表示」をクリックすると,下に入る。これで「OK」をクリック。
「2/5 品目分類(27年改定)」で「選択」をクリック,たくさんあるので右で「アイスクリーム」を検索。「356 アイスクリーム・シャーベット」が見つかるので,それを選択し,「選択項目表示」をクリックすると,下に入る。これで「OK」をクリック。
同様に,「3/5 世帯区分」で「二人以上の世帯(2000年〜)」,「4/5 地域区分」で「全国」,「5/5 時間軸(月次)」では「全項目表示」。
「表示位置」については,「品目分類」を「列1」,「時間軸(月次)」を「行1」にし,「レイアウトイメージの確認」をクリックして確認。
「ダウンロード」をクリックし,CSV形式でダウンロードする。
東京の気象データについては,気象庁Webページ『過去の気象データ』が出典と書かれているので,検索して過去の気象データ・ダウンロードのページに行く。
「地点を選ぶ」で「東京」を選ぶ。
「項目を選ぶ」で,データの種類「月別値」,項目「日最高気温の月平均」「降水量の月合計」「月平均相対湿度」「日最高気温25℃以上の日数(月)」を選ぶ。
「期間を選ぶ」で2003年1月〜2012年12月を選ぶ。
「CSVファイルをダウンロード」をクリックする。
CSVファイルはRでもExcelで開ける。Excelのほうが慣れている人は,Excelで使いやすいように整形するのがわかりやすいであろう。
念のため,このようにして得た世帯あたりアイスクリーム・シャーベットの消費金額を icecream.csv,東京の気象を tokyo-weather-2003-2012.csv として置いておいた(いずれもShift JIS)。いずれもRで読みやすいように整形してある。
ここでは整形したデータを読む方法を書いておく:
icecream = read.csv("https://okumuralab.org/~okumura/stat/data/icecream.csv", comment.char="#", fileEncoding="CP932")
tokyo = read.csv("https://okumuralab.org/~okumura/stat/data/tokyo-weather-2003-2012.csv", fileEncoding="CP932")
データによっては日あたりの量に直す必要があるので,年・月を与えるとその月の日数を求める関数が必要になる。例えば次のようにすればよい。
days = function(year, month) {
m = c(31,28,31,30,31,30,31,31,30,31,30,31)
m[month] + ((month == 2) && ((year %% 4 == 0) && (year %% 100 != 0) || (year %% 400 == 0)))
}
プロットは例えば次のようになる。
x = tokyo[,3] y = icecream[,3]/days(icecream$年,icecream$月) plot(x, y, pch=16, xlab="平均最高気温(℃)", ylab="アイスクリーム購入額(円)")
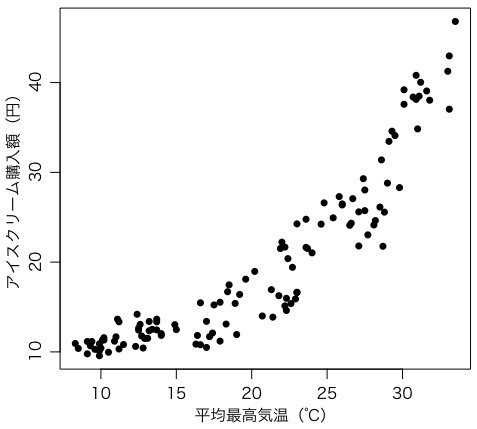
これらの点を最小2乗法でまず1次式でフィットしてみよう。
> r1 = lm(y ~ x)
> summary(r1)
Call:
lm(formula = y ~ x)
Residuals:
Min 1Q Median 3Q Max
-7.7978 -2.8211 0.0065 2.6202 11.6664
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -3.77290 1.07910 -3.496 0.000666 ***
x 1.16158 0.04999 23.236 < 2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 4.064 on 118 degrees of freedom
Multiple R-squared: 0.8206, Adjusted R-squared: 0.8191
F-statistic: 539.9 on 1 and 118 DF, p-value: < 2.2e-16
実際に直線を描き込むには abline(r1) と打ち込む。
2次式でフィットしてみよう。
> r2 = lm(y ~ x + I(x^2))
> summary(r2)
Call:
lm(formula = y ~ x + I(x^2))
Residuals:
Min 1Q Median 3Q Max
-8.7083 -1.6025 0.1931 1.8113 5.3939
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 20.664368 1.981857 10.427 < 2e-16 ***
x -1.596552 0.212165 -7.525 1.19e-11 ***
I(x^2) 0.067540 0.005136 13.149 < 2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 2.593 on 117 degrees of freedom
Multiple R-squared: 0.9276, Adjusted R-squared: 0.9264
F-statistic: 749.7 on 2 and 117 DF, p-value: < 2.2e-16
> curve(0.067540 * x^2 - 1.596552 * x + 20.664368, add=TRUE)
同様に3次式以上でもフィットしてみよう。何次式が一番適切か。
> r3 = lm(y ~ x + I(x^2) + I(x^3)) > AIC(r1, r2, r3) df AIC r1 3 681.0563 r2 4 574.1705 r3 5 570.2895
ダウンロードしたファイルをRで直接読むこともできる。これが本来は望ましい(手作業が入らないので)。おおよそ次のようにすればよい(ファイル名はご自分のものに直してください)。fileEncoding="SJIS" はWindowsではデフォルトなので省略可。
x = read.csv("気象.csv", header=FALSE, fileEncoding="SJIS", skip=7)
y = read.csv("アイスクリーム.csv", header=FALSE, fileEncoding="SJIS", skip=11)
y$V1 = NULL
y$V2 = NULL
y$V3 = gsub("月", "", gsub("年", "/", y$V3))
y$V4 = as.numeric(gsub("[,*]", "", y$V4))
z = merge(x, y, by.x="V1", by.y="V3")
z$年 = gsub("/.*", "", z$V1)
z$月 = gsub(".*/", "", z$V1)