臨床研究いろはにほという本は,臨床研究に必要な考え方をうまくまとめてある本です。そこに,例えばA治療(イベント発症率10%)とB治療(イベント発症率20%)を比較し,B治療の有効性を証明するのに必要な症例数が片群273例(α過誤5%,β過誤10%)であることが書いてありますが,計算のしかたが書いてありません。Rではどのようにすればよいでしょうか。なお,α過誤5%ということは有意水準を0.05にすることを意味し,β過誤10%ということは検出力(power)が0.9つまり仮定した効果があれば9割の確率で有意な結果が出ることを意味します。
Rには標準で power.prop.test() という関数が備わっています。これを使えば,
power.prop.test(p1=0.1, p2=0.2, power=0.9, strict=TRUE)Two-sample comparison of proportions power calculationn = 265.8559p1 = 0.1p2 = 0.2sig.level = 0.05power = 0.9alternative = two.sidedNOTE: n is number in *each* group
つまり片群で266例あればよいことになります(この場合 strict=TRUE がなくても結果はほとんど変わりません)。
また,pwrパッケージにも同様な関数 pwr.2p.test() や,両群のサイズが異なる場合にも使える pwr.2p2n.test() があります。
library(pwr)pwr.2p.test(ES.h(0.1,0.2), power=0.9)Difference of proportion power calculation for binomial distribution (arcsine transformation)h = 0.2837941n = 260.9272sig.level = 0.05power = 0.9alternative = two.sidedNOTE: same sample sizes
片群で261例あればよいことになります。どちらの結果も,最初に挙げた本とは少しだけ違います。本はどういうソフトで計算したのでしょうか。
青木先生の標本の大きさの決定の二群の比率の差の検定のときに計算式やRコードが書いてあります。やってみると,R標準の power.prop.test()(strict=TRUE なし)と同じ結果になりました。
シミュレーションを使って,もっと正確な結果を求めてみましょう。元となる検定には fisher.test() を使うことにします。速さを考えていない素朴なコードです。無駄に回数を多くしていますが,1000回か10000回でも十分です。
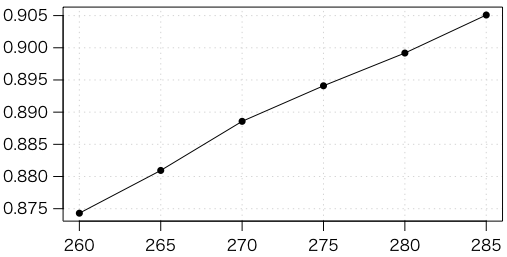
foo = function(n) {n1 = rbinom(1, n, 0.1)n2 = n - n1n3 = rbinom(1, n, 0.2)n4 = n - n3fisher.test(matrix(c(n1,n2,n3,n4), nrow=2))$p.value}p = replicate(1000000, foo(260)); mean(p <= 0.05) # 0.874301p = replicate(1000000, foo(265)); mean(p <= 0.05) # 0.880944p = replicate(1000000, foo(270)); mean(p <= 0.05) # 0.888573p = replicate(1000000, foo(275)); mean(p <= 0.05) # 0.894095p = replicate(1000000, foo(280)); mean(p <= 0.05) # 0.899182p = replicate(1000000, foo(285)); mean(p <= 0.05) # 0.905091
グラフを描くと次のようになり,検出力0.9を得るにはだいたい280症例くらい必要なことがわかります。

Last modified: