津田敏秀さんの「有病オッズ比」は以前とまるで違う - Togetterまとめ に触発されて書いた。
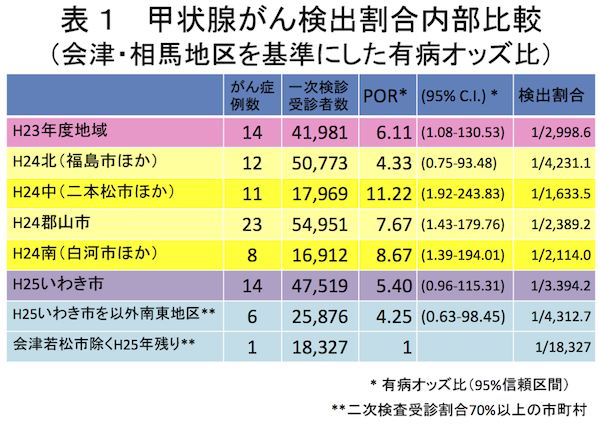
環境省第8回東京電力福島第一原子力発電所事故に伴う住民の健康管理のあり方に関する専門家会議(2014-07-16)の (津田敏秀氏提出資料) [PDF 1,993KB] のp.5表1では5%水準で有意であった4個の値が,第4回市民科学者国際会議(2014-11-23)の津田先生のスライド(PDF)のp.20表3ではすべて有意でなくなっている。

例えば上の「表1」で,一番下(オッズ = 1/(18327-1))を基準とした一番上(オッズ = 14/(41981-14))の有病オッズ比(POR: prevalence odds ratio)は (14/(41981-14)) / (1/(18327-1)) = 6.11 である。
まず,この4つの数値をRの行列の形で表しておく:
> x = matrix(c(14,1,41981-14,18327-1), ncol=2)
> x
[,1] [,2]
[1,] 14 41967
[2,] 1 18326
> (x[1,1]/x[1,2]) / (x[2,1]/x[2,2])
[1] 6.11347
2×2の表でオッズ比の信頼区間を計算する方法はいろいろある。フィッシャーの正確検定では信頼区間は [0.93, 258.25] である(ただしこの方法ではオッズ比の定義が上の計算とほんの少し違うことと,信頼区間と p 値を別の方法で計算していることに注意):
> fisher.test(x)
Fisher's Exact Test for Count Data
data: x
p-value = 0.04958
alternative hypothesis: true odds ratio is not equal to 1
95 percent confidence interval:
0.9299934 258.2508992
sample estimates:
odds ratio
6.113568
Epiパッケージの twoby2() による信頼区間は [0.80, 46.49] である:
> library(Epi)
> twoby2(x)
2 by 2 table analysis:
------------------------------------------------------
Outcome : Col 1
Comparing : Row 1 vs. Row 2
Col 1 Col 2 P(Col 1) 95% conf. interval
Row 1 14 41967 3e-04 2e-04 6e-04
Row 2 1 18326 1e-04 0e+00 4e-04
95% conf. interval
Relative Risk: 6.1118 0.8038 46.4742
Sample Odds Ratio: 6.1135 0.8039 46.4940
Probability difference: 0.0003 0.0000 0.0005
Asymptotic P-value: 0.0803
------------------------------------------------------
epitoolsパッケージの oddsratio.wald() による信頼区間も同じ(出力が長いので信頼区間以外を省略した):
> library(epitools)
> oddsratio.wald(x)
...
odds ratio with 95% C.I.
Predictor estimate lower upper
Exposed1 1.00000 NA NA
Exposed2 6.11347 0.803856 46.49404
...
同じくepitoolsパッケージの oddsratio.midp() では [1.08, 130.87] となる:
> oddsratio.midp(x)
...
odds ratio with 95% C.I.
Predictor estimate lower upper
Exposed1 1.00000 NA NA
Exposed2 5.39444 1.082926 130.8747
...
5%水準で有意となる(95%信頼区間が 1 を含まない)のは最後の oddsratio.midp() だけである。津田先生が使っておられるのも,おそらくこれだと思われる(一部微妙な違いがあるが,使用ソフトの違いであろう)。
なお,oddsratio.midp() は良い方法であるので,津田先生がこれを選ばれたことは妥当である。
これ以外にvcdパッケージ,fmsbパッケージについて中澤先生に教えていただいた(2×2の表,オッズ比,相対危険度参照)。これらをまとめると次のようになる:
| パッケージ | 関数 | p値 | オッズ比 | 95%信頼区間 |
|---|---|---|---|---|
| (津田) | - | - | 6.11 | [1.08, 130.53] |
| - | chisq.test() | 0.08596 | - | - |
| - | chisq.test(correct=FALSE) | 0.04573 | - | - |
| - | fisher.test() | 0.04958 | 6.113568 | [0.9299934, 258.2508992] |
| Epi | twoby2() | 0.0803 | 6.1135 | [0.8039, 46.4940] |
| epitools | oddsratio.wald() | - | 6.11347 | [0.803856, 46.49404] |
| epitools | oddsratio.midp() | 0.03731035 | 5.39444 | [1.082926, 130.8747] |
| epitools | oddsratio.fisher() | 0.04957872 | 6.113568 | [0.9299934, 258.2509] |
| epitools | oddsratio.small() | - | 3.056662 | [0.7858456, 22.6751] |
| vcd | oddsratio() | 0.08028 | 6.11347 | [0.803856, 46.49404] |
| fmsb | oddsratio() | 0.04574 | 6.11347 | [0.803856, 46.494045] |
| exact2x2 | fisher.exact() | 0.04958 | 6.113568 | [1.0092, 127.4884] |
| exact2x2 | blaker.exact() | 0.04958 | 6.113568 | [1.0092, 127.4884] |
表が全体として有意か(この場合は「オッズがすべて等しい」という帰無仮説が棄却できるか)を検定する前に,特定の比較を検定することはまずいとされている。特に,この場合は各オッズ比が独立でないので,全体として有意でなくても,有意なオッズ比がいくつも出ることがある。
まず,表全体を行列の形にする:
> a = matrix(c(14,12,11,23,8,14,6,1,
41981-14,50773-12,17969-11,54951-23,16912-8,47519-14,25876-6,18327-1),
ncol=2)
> a
[,1] [,2]
[1,] 14 41967
[2,] 12 50761
[3,] 11 17958
[4,] 23 54928
[5,] 8 16904
[6,] 14 47505
[7,] 6 25870
[8,] 1 18326
まずフィッシャーの正確検定。デフォルトの設定(workspace=200000)ではメモリが足りないといわれるので,順次増やしてみた:
> fisher.test(a)
以下にエラー fisher.test(a) : FEXACT error 40.
Out of workspace.
> fisher.test(a, workspace=2000000)
以下にエラー fisher.test(a, workspace = 2e+06) : FEXACT error 7.
LDSTP is too small for this problem.
Try increasing the size of the workspace.
> fisher.test(a, workspace=20000000)
以下にエラー fisher.test(a, workspace = 2e+07) : FEXACT error 7.
LDSTP is too small for this problem.
Try increasing the size of the workspace.
> fisher.test(a, workspace=200000000)
Fisher's Exact Test for Count Data
data: a
p-value = 0.05154
alternative hypothesis: two.sided
ぎりぎり5%で有意ではない。念のため,メモリ制約を受けないカイ2乗検定もしてみる:
> chisq.test(a)
Pearson's Chi-squared test
data: a
X-squared = 13.393, df = 7, p-value = 0.06309
こちらも有意ではない。
結論として,全体として有意ではない表から,有意な部分を探してしまったということであろう。
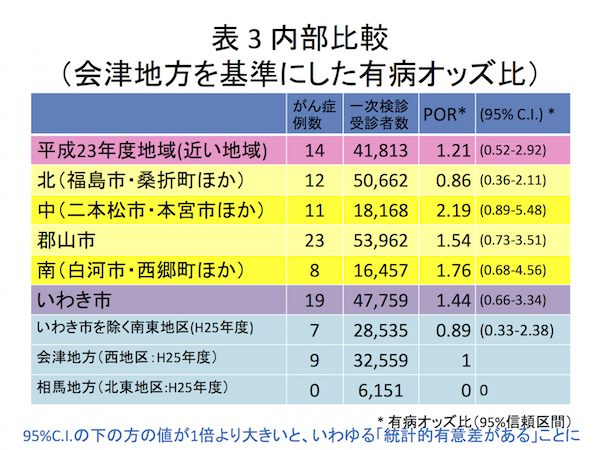
念のため,「表3」のほうも有意でない:
> b = matrix(c(14,12,11,23,8,19,7,9,0,
41813-14,50662-12,18168-11,53962-23,16457-8,47759-19,28535-7,32559-9,6151-0),
ncol=2)
> b
[,1] [,2]
[1,] 14 41799
[2,] 12 50650
[3,] 11 18157
[4,] 23 53939
[5,] 8 16449
[6,] 19 47740
[7,] 7 28528
[8,] 9 32550
[9,] 0 6151
> fisher.test(b, workspace=200000000)
Fisher's Exact Test for Count Data
data: b
p-value = 0.2181
alternative hypothesis: two.sided
> chisq.test(b)
Pearson's Chi-squared test
data: b
X-squared = 10.9629, df = 8, p-value = 0.2038
警告メッセージ:
In chisq.test(b) : カイ自乗近似は不正確かもしれません
Last modified: