土壌くんのシミュレーションの生データ(Excel)の2番目のシートの土壌くん③のデータを使う。
対応するCs合計は,1cmきざみと2cmきざみがあるが,平均により2cmきざみに揃える。
Cs = matrix(c(
6364.85,7847.05,7833.495,6000.22,447.65,494.695,289.51,200.095,
14113.99,9284.075,5577.745,4291.49,1956.93,353.665,214.72,78.845,
15402.78,19169.57,19094.7,11076.2,11703.44,7886.545,4650.63,1238.135,
35823.08,17280.22,7036.76,3178.84,2898.075,1288.67,368.945,NA,
15247.82,6331.12,1587.76,609.2,257.71,160.6,61.495,36.96,
3514.46,3667.29,2459.04,2916.48,1365.365,5538.525,5255.265,2317.53,
41202.48,15141.6,1264.95,174.29,128.94,77.44,56.965,41.84,
37812.07,16320.27,6042.08,6959.605,4507.375,3708.685,1739.52,162.285,
16416.25,9282.32,3511.935,1144.685,518.215,62.025,42.69,26.015,
13157.43,17074.59,4834.12,1538.895,352.485,216.445,33.805,28.62,
6910.925,6505.695,3127.415,586.05,563.51,76.45,30.755,21.69,
34336.01,14011.3,2090.2,1390.38,456.36,375.9,328.285,98.025,
3235.88,2163.925,2467.895,1205.8,20.83,21.645,21.35,20.18,
# ここまでが1cmきざみを2cmきざみに平均してまとめたもの
4920.47,6546.18,7799.19,2839.07,7197.74,1596.74,266.95,225.56,
6973.68,10222.80,8943.78,5162.30,563.85,281.12,812.69,206.65,
2110.94,1503.61,6378.80,9525.98,6061.84,3896.05,1436.46,115.75,
12836.19,8323.08,1034.07,2323.59,2910.66,937.74,41.71,33.38,
15971.04,17587.94,9388.56,2974.05,495.45,93.45,20.47,20.17,
2644.94,6291.39,12883.72,10208.42,5359.22,2770.07,1280.00,911.09,
5078.13,5038.02,2038.57,1248.33,627.48,539.51,614.60,517.73,
2292.88,775.37,500.00,44.98,166.40,560.71,32.68,23.76,
14231.60,13076.92,5022.22,1329.08,182.55,167.75,64.65,26.70,
7788.94,3687.53,90.57,164.33,72.57,119.18,48.67,65.10,
16570.05,14245.94,548.61,76.14,63.48,91.43,36.31,37.03,
9035.62,9881.58,2889.89,225.64,175.44,97.37,23.21,18.26,
5623.38,4207.22,2433.93,2677.09,1552.04,901.71,98.68,15.18,
14806.48,9925.56,1687.81,389.89,82.58,344.04,81.72,87.09,
16482.62,19902.44,1318.82,170.27,155.09,100.71,66.77,66.62,
5920.48,543.39,231.74,82.99,57.65,62.55,51.77,29.77,
11452.99,9744.60,5009.42,1414.97,1504.36,1802.68,556.37,85.44,
10382.29,2792.51,843.60,382.50,114.94,26.98,17.80,22.61,
13071.90,13020.24,2796.09,259.32,476.54,2081.32,67.43,29.31,
3232.29,4337.09,2712.35,3543.62,4309.25,3730.87,3008.21,708.20,
13134.57,7937.74,1435.31,1038.37,380.42,412.96,196.35,49.34,
11929.03,4543.76,2436.70,155.80,78.31,39.18,17.07,19.14,
15831.13,23790.17,5791.22,1328.70,72.59,37.85,44.92,27.76,
2127.24,7927.73,2037.90,466.09,120.37,52.85,149.17,67.94,
13571.10,1739.59,90.88,38.54,36.65,29.64,63.16,31.57,
9203.77,6443.82,2459.88,1092.50,1368.50,5146.28,1403.56,33.77,
37708.65,24046.24,3748.44,771.78,793.36,52.29,46.90,19.30,
6062.87,176.96,46.61,214.72,149.95,50.16,80.22,18.23,
13388.80,8935.85,1923.76,443.26,146.81,80.54,41.71,35.91,
24555.00,22207.04,7021.19,490.41,1195.10,203.63,66.46,97.94,
6318.25,1522.63,360.06,478.29,344.13,592.68,211.38,887.13,
33806.82,6454.82,2062.74,1772.73,6380.15,1040.12,94.32,65.67,
10183.07,1975.70,706.80,318.90,202.28,62.92,68.66,17.40,
8117.30,976.43,739.23,218.44,140.96,37.01,17.29,17.45,
16253.44,2420.44,376.23,129.36,854.12,903.02,123.36,64.44,
10117.15,8847.06,4886.41,576.92,236.37,122.68,23.67,37.49), nrow=8)
cpm = matrix(c(
67.37,88.16,91.84,78.77,
58.32,84.13,100.22,85.81,
56.31,86.15,92.51,96.2,
64.36,63.35,51.28,37.21,
63.35,79.44,59.33,43.91,
44.25,55.64,51.62,60.67,
84.13,56.31,47.26,39.55,
103.58,103.24,93.52,77.77,
84.47,68.38,57.99,38.88,
71.4,55.31,48.27,40.89,
57.99,48.27,44.92,49.61,
89.5,76.42,60,44.92,
55.98,49.61,37.21,33.52,
65.03,79.44,89.16,86.82,
59.66,88.83,80.45,61.34,
48.94,64.69,69.39,62.01,
57.32,72.74,51.96,42.57,
51.96,69.39,62.68,47.93,
103.24,93.52,84.8,75.75,
36.87,51.28,41.23,55.98,
53.97,79.44,47.93,52.29,
36.54,55.31,51.62,49.94,
45.25,49.94,37.21,42.23,
53.3,82.46,50.95,46.59,
50.95,62.35,48.27,38.55,
40.56,55.98,48.27,39.89,
61.01,52.29,39.22,35.87,
78.44,82.12,91.51,58.66,
102.57,65.7,47.6,39.89,
90.84,78.77,76.42,60.34,
67.04,47.93,43.58,30.5,
72.4,66.7,62.35,47.6,
58.66,40.89,53.63,52.29,
91.84,81.12,61.68,53.97,
61.68,41.9,43.91,32.85,
79.78,61.34,53.97,45.59,
78.44,84.13,74.75,50.28,
104.58,101.9,69.39,54.64,
69.05,65.03,62.68,60,
97.21,74.08,52.29,43.91,
63.69,51.96,41.23,38.55,
88.83,70.39,52.96,46.93,
91.51,88.16,76.42,48.27,
73.41,52.29,48.27,43.58,
79.44,76.09,50.95,40.89,
84.8,60,44.92,36.54,
56.65,45.92,33.18,31.17,
76.09,61.01,54.64,43.58,
72.74,67.37,48.27,42.57), nrow=4)
これで重み付き最小2乗法:
lm(cpm[1,] ~ Cs[1,]+Cs[2,]+Cs[3,]+Cs[4,]+Cs[5,]+Cs[6,]+Cs[7,]+Cs[8,]-1,
weights=1/cpm[1,])
lm(cpm[2,] ~ Cs[1,]+Cs[2,]+Cs[3,]+Cs[4,]+Cs[5,]+Cs[6,]+Cs[7,]+Cs[8,]-1,
weights=1/cpm[2,])
lm(cpm[3,] ~ Cs[1,]+Cs[2,]+Cs[3,]+Cs[4,]+Cs[5,]+Cs[6,]+Cs[7,]+Cs[8,]-1,
weights=1/cpm[3,])
lm(cpm[4,] ~ Cs[1,]+Cs[2,]+Cs[3,]+Cs[4,]+Cs[5,]+Cs[6,]+Cs[7,]+Cs[8,]-1,
weights=1/cpm[4,])
安定しないので,深いところのデータは平均してまとめる:
Cs4 = matrix(nrow=4, ncol=49)
for (i in 1:49) {
for (j in 1:3) Cs4[j,i] = Cs[j,i]
Cs4[4,i] = mean(Cs[4:8,i], na.rm=TRUE)
}
lm(cpm[1,] ~ Cs4[1,]+Cs4[2,]+Cs4[3,]+Cs4[4,]-1, weights=1/cpm[1,])
lm(cpm[2,] ~ Cs4[1,]+Cs4[2,]+Cs4[3,]+Cs4[4,]-1, weights=1/cpm[2,])
lm(cpm[3,] ~ Cs4[1,]+Cs4[2,]+Cs4[3,]+Cs4[4,]-1, weights=1/cpm[3,])
lm(cpm[4,] ~ Cs4[1,]+Cs4[2,]+Cs4[3,]+Cs4[4,]-1, weights=1/cpm[4,])
係数行列(応答行列)を A に求める(Aは溝口先生の記法ではinv(P)):
A = matrix(c(
lm(cpm[1,] ~ Cs4[1,]+Cs4[2,]+Cs4[3,]+Cs4[4,]-1, weights=1/cpm[1,])$coefficients,
lm(cpm[2,] ~ Cs4[1,]+Cs4[2,]+Cs4[3,]+Cs4[4,]-1, weights=1/cpm[2,])$coefficients,
lm(cpm[3,] ~ Cs4[1,]+Cs4[2,]+Cs4[3,]+Cs4[4,]-1, weights=1/cpm[3,])$coefficients,
lm(cpm[4,] ~ Cs4[1,]+Cs4[2,]+Cs4[3,]+Cs4[4,]-1, weights=1/cpm[4,])$coefficients),
nrow=4, byrow=TRUE)
結果として次の A が求まった:
[,1] [,2] [,3] [,4]
[1,] 0.0025416933 0.001003562 0.001556662 0.003992312
[2,] 0.0018983705 0.001125959 0.003356154 0.005461906
[3,] 0.0012633461 0.001124716 0.003463233 0.006906500
[4,] 0.0008627175 0.001062296 0.002452436 0.009024239
この逆行列は solve(A) と打ち込めば次のようになる:
[,1] [,2] [,3] [,4]
[1,] -1775.9788 6797.738 -7493.089 2406.0391
[2,] 10246.1790 -30537.202 32986.478 -11295.7699
[3,] -1338.1868 3416.210 -3002.744 822.4396
[4,] -672.6873 2016.457 -2350.664 986.9797
やはり負の値が多く,安定していないことがわかる。
逆に,CPM値からCs総量(Bq/kg)を求めるための係数行列 P を求めるには,次の最小2乗法を行う。ただし,重みを何にするかは問題である。重みを考えなければ,次のようになる:
P = matrix(c(
lm(Cs4[1,] ~ cpm[1,]+cpm[2,]+cpm[3,]+cpm[4,]-1)$coefficients,
lm(Cs4[2,] ~ cpm[1,]+cpm[2,]+cpm[3,]+cpm[4,]-1)$coefficients,
lm(Cs4[3,] ~ cpm[1,]+cpm[2,]+cpm[3,]+cpm[4,]-1)$coefficients,
lm(Cs4[4,] ~ cpm[1,]+cpm[2,]+cpm[3,]+cpm[4,]-1)$coefficients),
nrow=4, byrow=TRUE)
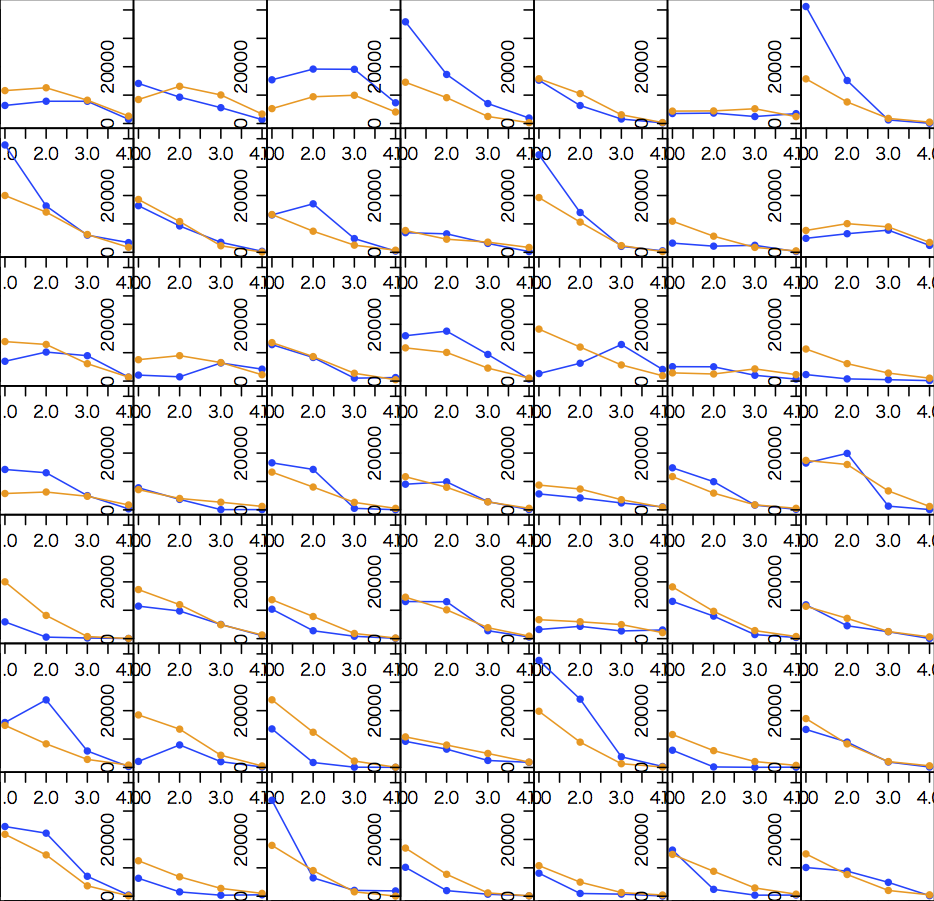
これで,ものすごく手抜きの図を描いてみる。青は真のCs総量,オレンジは推定値である。
par(mgp=c(2,0.8,0))
par(mar=c(0,0,0,0)) # orig: c(5,4,4,2)+0.1
par(mfrow=c(7,7))
for (i in 1:49) {
plot(1:4, Cs4[,i], type="o", pch=16, ylim=c(0,42000), xlab="", ylab="", col="#0041ff")
points(1:4, P %*% cpm[,i], type="o", pch=16, col="#ff9900")
}

Last modified: