[2014年11月15日いわき生涯学習プラザでのトークの最後の部分を拡張したものです]
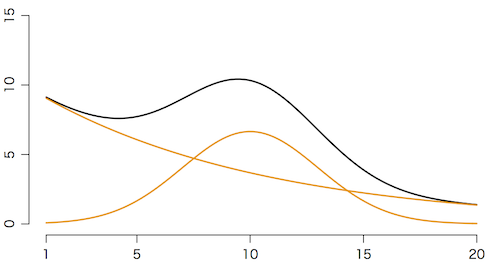
平均10,標準偏差3の正規分布の密度関数 $\frac{1}{\sqrt{2\pi}\cdot 3} e^{-(x-10)^2/(2\cdot 3^2)}$ と指数関数 $e^{-x/10}$ とを $50:10$ で混ぜ合わせた簡単な関数を考えます:
\[ \mu(x) = \frac{50}{\sqrt{2\pi}\cdot 3} e^{-(x-10)^2/(2\cdot 3^2)} + 10e^{-x/10} \]
$x = 1,2,\ldots,20$ について,上の式で与えられる値を平均値とするポアソン分布 $\displaystyle p_y = \frac{\mu^y e^{-\mu}}{y!}$ の乱数 $y$ を発生します:
f = function(x) { 50*dnorm(x,10,3) + 10*exp(-x/10) }
y = sapply(1:20, function(x){rpois(1,f(x))})
以下では次のような乱数ができたとします:
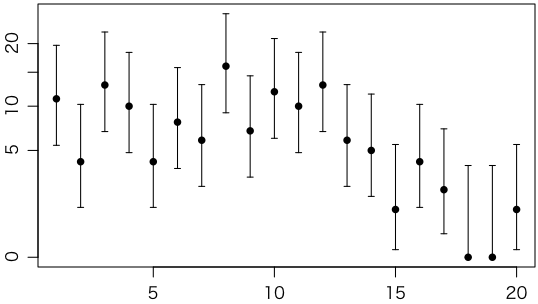
y = c(11,4,13,10,4,8,6,16,7,12,10,13,6,5,1,4,2,0,0,1)
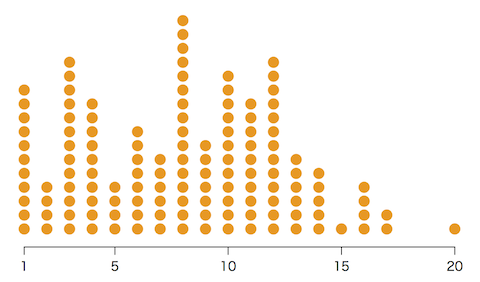
データと95%信頼区間をグラフにしてみましょう:
ci = sapply(1:20, function(i){poisson.test(y[i])$conf.int})
plot(1:20, y, type="p", pch=16, xlab="", ylab="", ylim=range(ci))
arrows(1:20, ci[1,], 1:20, ci[2,], length=0.03, angle=90, code=3)
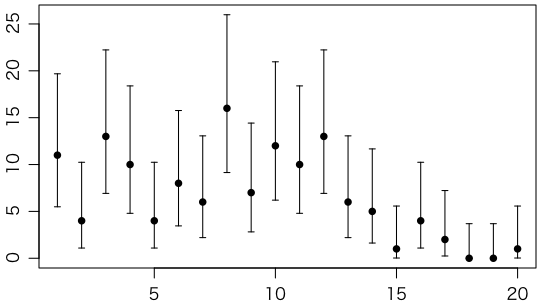
よく片対数グラフにすることがあります。ただ,対数だとカウント0が表示できません。
plot(1:20, y, type="p", pch=16, xlab="", ylab="", ylim=range(c(1,ci[2,])), log="y")
arrows(1:20, ci[1,], 1:20, ci[2,], length=0.03, angle=90, code=3)
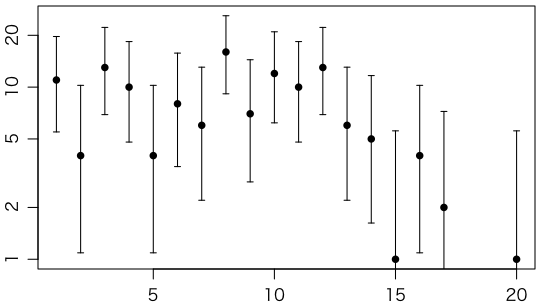
折衷案として,ポアソン分布の性質を使って縦軸を平方根にしたルートグラム(rootogram)はどうでしょうか。
plot(1:20, sqrt(y), type="p", pch=16, xlab="", ylab="", yaxt="n", ylim=sqrt(range(ci)))
arrows(1:20, sqrt(ci[1,]), 1:20, sqrt(ci[2,]), length=0.03, angle=90, code=3)
axis(2, sqrt(c(0,5,10,15,20)), c(0,5,10,15,20))
上のデータは
\[ \mu_i = \frac{a}{\sqrt{2\pi}\cdot 3} e^{-(x_i-10)^2/(2\cdot 3^2)} + be^{-x_i/10} \]という形の式で $a=50$,$b=10$ と置いたものから導かれたものです(このページの以前のバージョンでは $a$ と $b$ を逆にしていましたが,activity,background との語呂合せのため,このように変更しました。)。しかし,実際には $a$,$b$ は知られていません。データからこれらのパラメータの値を推測するのがフィッティングの問題です。
よく使われているのが,実測値 $y_i$ との差の2乗和
\[ \sum_{i=1}^{20} (y_i - \mu_i)^2 \]を最小にする $a$,$b$ を求める最小2乗法です。でもこれでは大きい値も小さい値も同じくらいがんばってフィットしようとします。でも,1 が 2 になるのと 1001 が 1002 になるのは同じくらい重要ではありません。そこで,大きい値の違いは小さい値の違いより軽く見る重み付き最小2乗法のほうがベターです。この方法は,この場合,実測値 $y_i$ の差の重み付き2乗和
\[ \sum_{i=1}^{20} \frac{(y_i - \mu_i)^2}{y_i} \]を最小にする $a$,$b$ を求めます。ただし,このままでは $y_i = 0$ があると使えません。そこで,$y_i = 0$ を無視したり,分割を荒くしてゼロになる階級(ビン)をなくしたり,分母を $y_i + 1$ にしたりして逃げます。
もっとよい方法は,データがポアソン分布から導かれたことを使って,最尤法(さいゆうほう)でパラメータを推定することです。具体的には,実測値 $y_i$ が得られる確率の積
\[ L = \prod_{i=1}^{20} \frac{\mu_i^{y_i} e^{-\mu_i}}{y_i!} \]を最大にする $a$,$b$ を求めます。もっとも,積は扱いにくいので,両辺の対数をとって足し算に直します。具体的には,対数尤度
\[ \log L = \sum_{i=1}^{20} (y_i \log \mu_i - \mu_i - y_i!) \]を最大にする $a$,$b$ を求めます。ただし,データ $y_i$ はパラメータに依存しないので,対数尤度の計算から省いて,
\[ \log L = \sum_{i=1}^{20} (y_i \log \mu_i - \mu_i) \]としてもかまいません。
誤差分布としてポアソン分布でなく正規分布を仮定すれば,$L = \prod \exp(-(y_i - \mu_i)^2 / 2\sigma^2) \times \text{定数}$ ですから,$\log L = -\sum (y_i - \mu_i)^2 / 2\sigma^2 + \text{定数}$ となり,最小2乗法に帰着します。
実際に上記の $\log L$ が最大になる点を求めてみましょう。ここではRの関数 optim() を使って $-\log L$ を最小化します。
x = 1:20
y = c(11,4,13,10,4,8,6,16,7,12,10,13,6,5,1,4,2,0,0,1)
d = dnorm(x, 10, 3)
e = exp(-x/10)
f = function(arg) {
a = arg[1]
b = arg[2]
mu = a * d + b * e
-sum(y * log(mu) - mu)
}
optim(c(50,10), f) # 初期値 (50,10) から出発(このあたりは適当)
点 $(a,b) = (57.14, 9.23)$ あたりで最小値 $-\log L = -144.5676$ をとることがわかります。
ところで,ここでは $a$ が信号(ピーク)で $b$ はバックグラウンドです。そこで,与えられた $a$ について,$b$ だけを調節して尤度を最大にした値を,$L(a)$ と書くことにします。$\log L(a)$ をプロットしてみましょう。ここでは $b$ についての1次元の最大化を optimize() という関数で行っています。第2引数 c(0,100) は $0 \leq b \leq 100$ の範囲で最大化することを意味します。
logL = function(a) {
optimize(function(b){sum(y*log(a*d+b*e)-(a*d+b*e))}, c(0,100), maximum=TRUE)$objective
}
plot(30:90, sapply(30:90,logL), type="l", xlab="a", ylab="log L(a)")
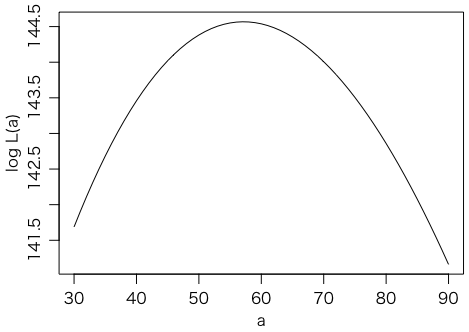
上に凸の放物線にとても近い曲線で,最大値はさきほど求めた $\log L = 144.5676$ に一致します。
あとで説明するように,$\log L$ が最大値から0.5だけ下がった点,つまり $\log L(a) = 144.5676 - 0.5$ の解 $a$ が,$\pm \sigma$(ほぼ68%信頼区間)に相当します。図から読み取るか,あるいは
uniroot(function(a){logL1(a)-(144.5676-0.5)}, c(40,60))
uniroot(function(a){logL1(a)-(144.5676-0.5)}, c(60,80))
で計算すれば,$[45.5, 69.3]$ が $a$ のほぼ68%信頼区間であることがわかります。同様に,最大値から $n^2/2$ だけ下がった点が $\pm n\sigma$ に相当する信頼区間になります。
なぜ0.5下がった点が68%信頼区間かは,有名なクラメール・ラオの不等式(Cramér–Rao inequality,名前にフレシェ Fréchet を加えることもあります)を使えば説明できます。不等式ですが,不偏(unbiased)かつ有効(efficient)な場合は等式になるので,ここでは等式で説明します。あるパラメータの推定量の分散は $V(\hat{\theta}) = 1 / I(\theta)$ つまりフィッシャー情報量 $I(\theta)$ の逆数になります。フィッシャー情報量は $I(\theta) = -E(\partial^2 \log L / \partial \theta^2)$ で表せますから,$\log L = -k\theta^2$ の形をしていれば…ここまで書けばもう証明できますね。
より簡単にRでポアソン分布による最尤法を計算するには,
x = 1:20
y = c(11,4,13,10,4,8,6,16,7,12,10,13,6,5,1,4,2,0,0,1)
のようにデータを設定して,
r = glm(y ~ dnorm(x,10,3) + exp(-x/10) - 1, family=poisson(link="identity"))
と打ち込むだけです。関数 glm() の名前は generalized linear model から来ています。ここでは結果を r というオブジェクトに代入していますので,r と打ち込めば結果が表示されます。もっと詳しい結果を表示するには summary(r) と打ち込みます。主な結果は次のようになります:
Coefficients:
Estimate Std. Error z value Pr(>|z|)
dnorm(x, 10, 3) 57.139 12.131 4.710 2.48e-06 ***
exp(-x/10) 9.234 1.566 5.897 3.70e-09 ***
これは,$a = 57.139 \pm 12.131$,$b = 9.234 \pm 1.566$ を意味します($\pm$ のあとは標準誤差です)。誤差の共分散行列は,vcov(r) と打ち込めば表示されます:
dnorm(x, 10, 3) exp(-x/10)
dnorm(x, 10, 3) 147.16953 -10.933472
exp(-x/10) -10.93347 2.451703
つまり,次の式でフィットできることがわかりました:
\[ \mu_i = \frac{57.139}{\sqrt{2\pi}\cdot 3} e^{-(x_i-10)^2/(2\cdot 3^2)} + 9.234e^{-x_i/10} \]カウント数に焼き直せば,sum(57.139 * dnorm(x,10,3)) で 57.08,sum(9.234 * exp(-x/10)) で75.92,合わせて 133 で,当然ながら全体の個数 sum(y) と一致します。
度数分布を使うと,どうしても横軸方向の分解能が限られてしまいます。ここでは度数分布を使わない方法を説明します。度数分布の一つ一つの区間を「ビン」(bin)というので,この方法は unbinned な(ビン分けしない)方法と呼ばれます。
例えば,さきほどの度数分布のデータ
x = 1:20
y = c(11,4,13,10,4,8,6,16,7,12,10,13,6,5,1,4,2,0,0,1)
は x が y 回ずつ繰り返されるので,
z = rep(x, y)
のように展開すれば,z は
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 5, 5, 5, 5, 6, 6, 6, 6, 6, 6, 6, 6, 7, 7, 7, 7, 7, 7, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 9, 9, 9, 9, 9, 9, 9, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 13, 13, 13, 13, 13, 13, 14, 14, 14, 14, 14, 15, 16, 16, 16, 16, 17, 17, 20
という133個の数値になります。これらは整数値しかとらないので度数分布にしても情報は失われませんが,整数に丸める前の実数値がわかれば,より大きな情報量(分解能)が得られます。しかし,以下では度数分布での計算と比較するために,整数値だけのデータ z を例に説明します。
まずは1次元の簡単な例から。さきほどのデータは指数関数と正規分布の密度関数を混ぜ合わせたものでしたが,データから両者の混合比を求めてみましょう。
まず,考えている区間で,両方の関数のグラフ下の面積を1に揃えます(規格化,normalization)。実際には定積分して1(あるいは一定の値)になるようにするのですが,ここでは整数のデータなので単純に和が1になるようにすればいいでしょう。具体的には,sum(exp(-x/10)) と打ち込むと答えは 8.221519 になるので,
が規格化された関数です。同様に,sum(dnorm(x,10,3) は 0.9990481 ですので,
が規格化された関数です。これらの混合
\[ L = \prod_{i=1}^{133} (tg(z_i) + (1-t)h(z_i)) \]が尤度関数になります。両辺の対数をとって
\[ \log L = \sum_{i=1}^{133} \log(tg(z_i) + (1-t)h(z_i)) \]を最大にします。
g = function(x) { exp(-x/10) / 8.221519 }
h = function(x) { dnorm(x,10,3) / 0.9990481 }
f = function(t) { sum(log(t * g(z) + (1-t) * h(z))) }
optimize(f, c(0,1), maximum=TRUE)
最大値は $f(0.5707911) = -372.8489$ であることがわかります。最大値付近のグラフは次のようになります。横線は最大値から 0.5 を引いたところです。
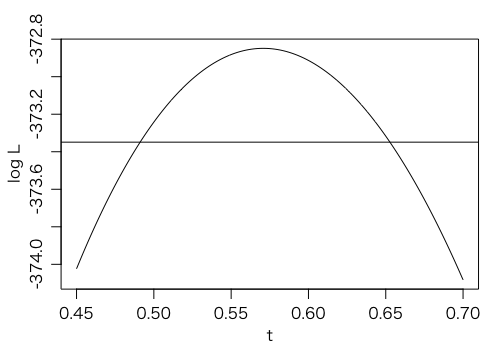
さきほど説明した理由により,対数尤度関数の最大値から 0.5 を引いたところの横軸 $0.57 \pm 0.08$ がほぼ $\pm \sigma$ 相当の誤差(およそ68%信頼区間)になります。交点を正確に求めるには次のコマンドが使えます。
uniroot(function(t){f(t)-(-372.8489-0.5)}, c(0,0.57))
uniroot(function(t){f(t)-(-372.8489-0.5)}, c(0.57,1))
ちなみに,全体の個数が133個の場合,0.5707911 * 133 を計算すると 75.92 になり,度数分布を使った方法と一致します。
さて,ここまでは全体の個数が133であるという情報を使いませんでした。これを使うには,尤度に全体の個数の分布を掛けなければなりません。個数の真の値を $\nu$,それぞれの部分の個数の真の値を $\nu_1 = \nu t$,$\nu_2 = \nu (1-t)$ とすると,
\[ L = \frac{\nu^{133} e^{-\nu}}{133!} \prod_{i=1}^{133} (tg(z_i) + (1-t)h(z_i)) = \frac{e^{-\nu_1-\nu_2}}{133!} \prod_{i=1}^{133} (\nu_1 g(z_i) + \nu_2 h(z_i)) \]となり,両辺の対数をとって定数を無視すれば
\[ \log L = \sum_{i=1}^{133} \log(\nu_1 g(z_i) + \nu_2 h(z_i)) - \nu_1 - \nu_2 \]これを $\nu_1$,$\nu_2$ について最大化します(ただし以下では $-\log L$ を最小化しています)。
f = function(arg) {
n1 = arg[1]
n2 = arg[2]
return(n1 + n2 - sum(log(n1 * g(z) + n2 * h(z))))
}
optim(c(50,50), f)
結果は,$(\nu_1,\nu_2) = (75.9, 57.1)$ で最大値 $144.5676$ になり,数値計算の誤差内で同じ結果が得られます。
誤差については $(\nu_1,\nu_2)$ 平面で等高線を描いて,最大値から 0.5 下がったところを見ればいいのですが,より簡便には,$\nu$ の誤差 $\pm \sqrt{\nu}$ と,$t$ の誤差 $\pm 0.08$ を独立と見て,正規分布側の誤差は $\sqrt{\nu} (1-t)$ と $0.08 \nu$ を三平方の定理で合成して,$\pm 11.74$ を得ます。度数分布を使った方法での誤差 $12.131 \times 57.08 / 57.139 \approx 12.12$ とだいたい近い値が得られます。等高線を見ても,/の方向の $\nu = \nu_1 + \nu_2$ と,\の方向の $t$ とが,ほぼ独立なことがわかります。
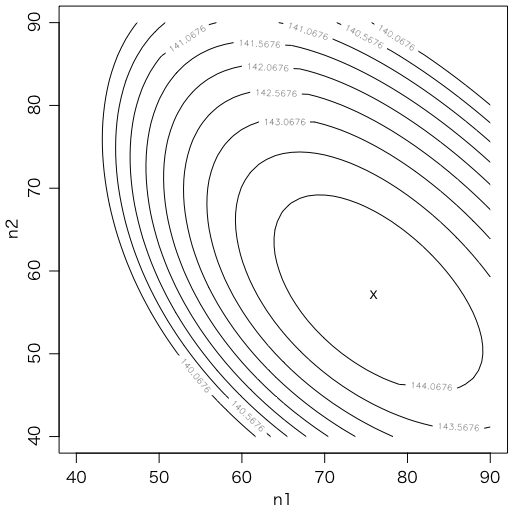
m = matrix(sapply(40:90, function(y){sapply(40:90, function(x){f(c(x,y))})}), nrow=51)
contour(40:90, 40:90, -m, levels=seq(144.5676,by=-0.5,length.out=10),
asp=1, xlab="n1", ylab="n2")
points(75.9, 57.1, pch="x")
別のやりかたとして,ヘッセ行列(Hessian)を推定して,その逆行列で分散・共分散行列を求めることもできます:
solve(optim(c(50,50), f, hessian=TRUE)$hessian)
この対角成分の平方根が各パラメータの標準誤差です。この方法による正規分布側の個数の標準誤差は 11.85 です。
Last modified: